TDCC Laboratory
TDCC 研究室
| HOME | ENGLISH |
3D スパイラル曲線
Joshua Gottdenker 氏(スウェーデン)、Svein Daniel Solvenus 氏(ノルウェー)、
浅井康之 氏(数学独学塾塾長)(東京都町田市)、山本信雄
|
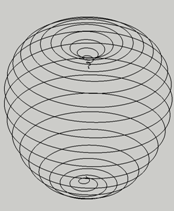
2011年1月にスウェーデンのジョシュア・ゴットデンカー氏(以下、ジョシュア氏)から 球面のスパイラル曲線を紹介され、 卵形曲線にも出来ないか、とのメールが寄せられました。山本がスパイラル曲線の式を作り、3次元(3D)における曲線の数値座標を計算しました。 それをエクセルファイルに書き込んだ結果を ジョシュア氏、および、同時期に山本と連絡があったスヴェイン・ダニエル・ソルヴェヌス氏 (以下、ダニエル氏)とのご協力を得て、3D画像を作成していただきました。卵形とリンゴ形の双方で行います。 1. 一般的表示
一般的な表示は、浅井康之氏(塾長室を参照)に教えていただきました。
それは次のような方法です。回転対称な閉曲線に対しては一般的と言えましょう。
2. 卵形スパイラル
(x, y)平面における卵形曲線の方程式は卵形曲線のページの(9b)式ですが、
上記(1)式の表示に従って、次のようにします。
|
|
|
|
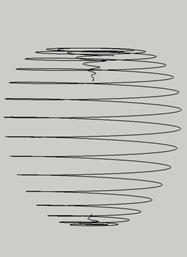
ジョシュア氏が作成の卵形スパイラル |
ダニエル氏が作成の卵形スパイラル |

|
|
|
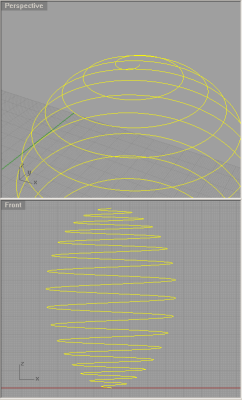
ジョシュアが作成の卵形スパイラル |
ダニエル氏が作成の卵形スパイラル |
|
3. リンゴ形スパイラル
(x, y)平面におけるリンゴ形曲線の方程式はリンゴ形曲線の方程式のページの(3)式ですが、
上記(1)と(2)式の手順に従って行い、次のリンゴ形スパイラルの式を作りました。
|
|
|
||||
|
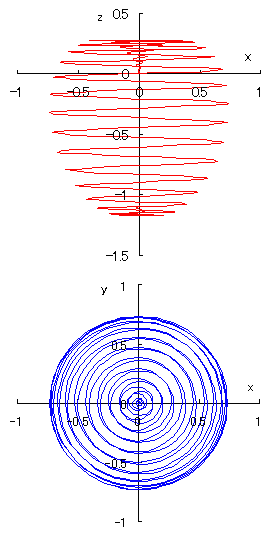
リンゴ形スパイラルの 正面図と平面図 |
|
|
~ブラウザの「戻る」で 前に開いたページに戻ります~
~または、下のボタンを押して HOME に戻ります~
| HOME |
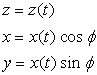 ,
(2)
,
(2)
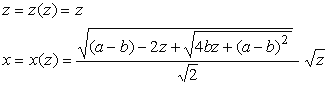 .
(4)
.
(4)
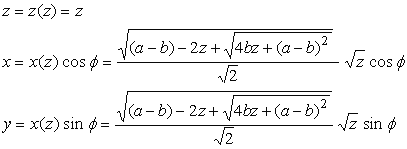 ,
(5)
,
(5)
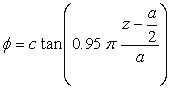 .
(7)
.
(7)
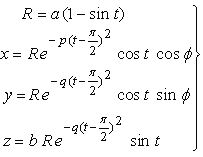 ,
(8)
,
(8)