
TDCC Laboratory
TDCC 研究室
| HOME | ENGLISH |
伊藤忠夫氏による卵形曲線の方程式
伊藤忠夫 氏(奈良県生駒市在住), 山本信雄
|
「卵形線」の数学的な定義は Ikuro 氏のサイト
「デルトイドの幾何学(その9)」の冒頭に書かれていますが、
ここでは、現実の鶏卵に近い形を与える曲線の方程式を追求し、その曲線を暫定的に「卵形曲線」と呼ぶことにします。
|
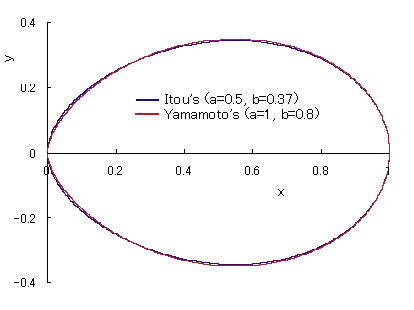
|
|
との比較。ただし、比較のため、伊藤氏のはx方向に a(=0.5) の値だけ平行移動させた。 |
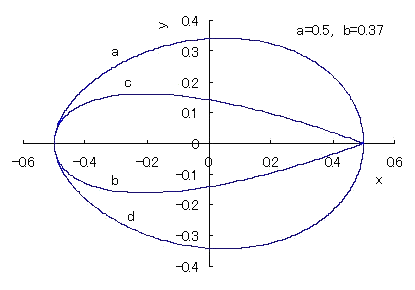
|
|
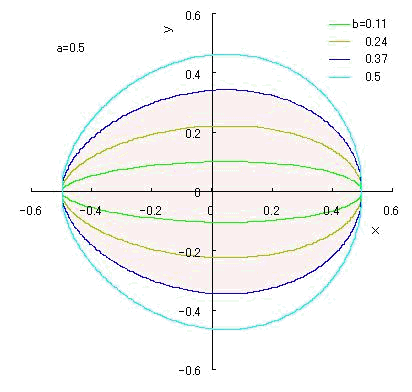
θ のすべての範囲を示した場合 各カーブ a, b, c, d については本文を参照のこと。 |
[参考] 図3の曲線を表す
|
|
図5 擬球を斜めに平面で切った断面の卵形曲線 |
|
図5において、2つの曲面
|
~ブラウザの「戻る」で 前に開いたページに戻ります~
~または、下のボタンを押して HOME に戻ります~
| HOME |
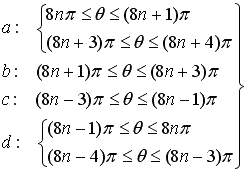 ,
(2)
,
(2)
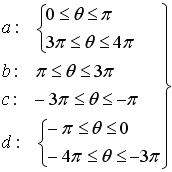 .
(2)'
.
(2)'
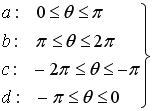 .
(2)''
.
(2)''
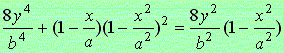 ,
(5)
,
(5)