TDCC Laboratory
TDCC 研究室
| HOME | ENGLISH |
浅井康之氏による卵形曲線の方程式
浅井康之氏(数学独学塾塾長)(東京都町田市), 山本信雄
浅井氏の提案による卵形曲線のご報告が、氏より寄せられました。
氏のご了承の上に、メールで戴いた資料をもとにして山本も計算を進め、再構成してみました。
|
本サイトは
Bounds of rotated egg? 、
塾長(校長) 室 、
【曲線-12】エッグカーブを描いてみよう 、
GENERATING AVIAN EGG USING RATIONAL BEZIER QUADRATIC CURVES
に紹介されています。
|
|
浅井氏の提案による新たな
卵形曲線(円を x 軸のプラス方向に徐々に引き伸ばす)の方程式
は次のとおりです。
なお、ここでは、変数 |
|
|
|
|
|
|
|
|
|
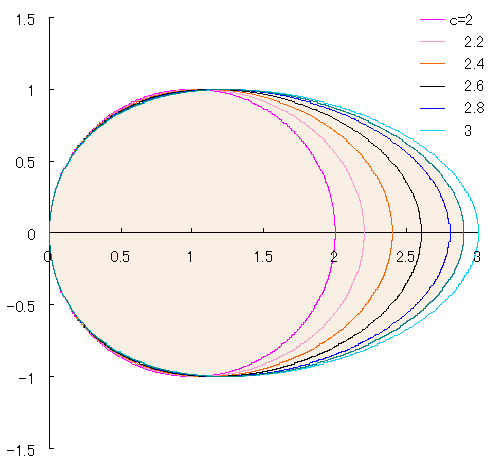
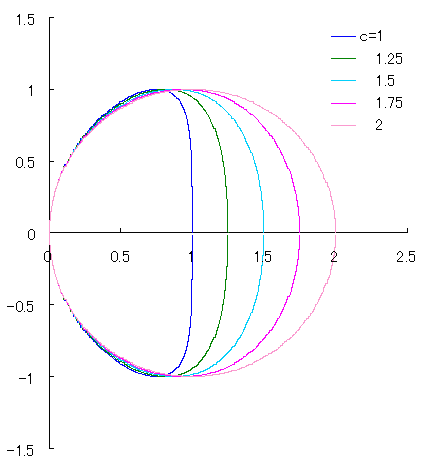
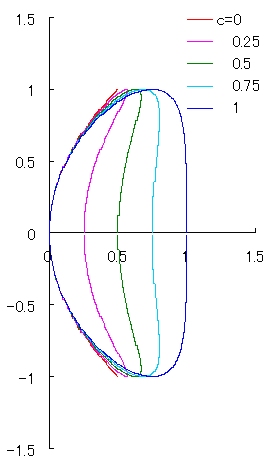
このように、図1の場合に卵形曲線が得られます。
|
 |
|
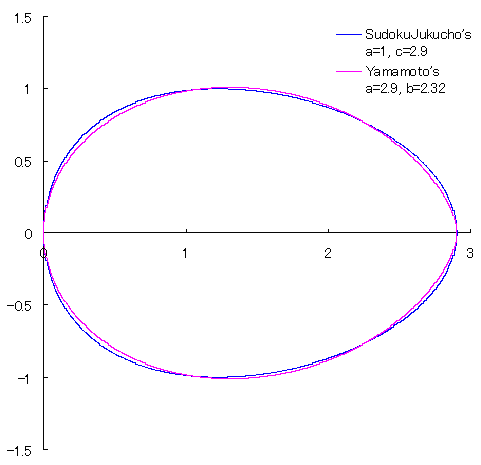
ただし、比較のため、山本のは座標の移動や左右の反転を行っている。 |
~ブラウザの「戻る」で 前に開いたページに戻ります~
~または、下のボタンを押して HOME に戻ります~
| HOME |