TDCC Laboratory
TDCC 研究室
| HOME | ENGLISH |
花の形のグラフィック
山本 信雄
本ページの図形は自由にコピーして自由にご使用できます。
|
|

|
|
1. はじめに
本サイトの別のページで取り扱った、カージオイドから作り出す「ハート形曲線 II」を花びらに応用して、ここに「花の形」をプログラミングにより作ることを試みます。そこでは2種の方法が書かれていますので、ここでも、その方法を踏襲して2種の方法を考えます。 2. 方法1
方法1は、カージオイドの丸い底の位相角を単純に狭めて角度を形成して、花びらとなるハート形を作ることです。 2.1 花びらとなるハート形曲線の伸縮がない場合
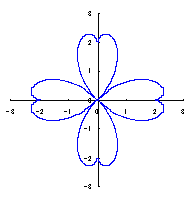
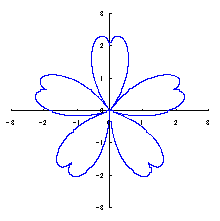
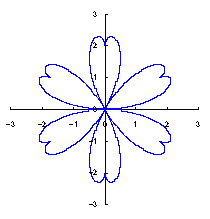
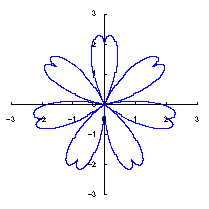
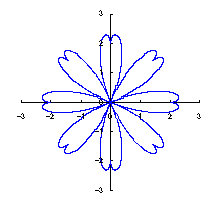
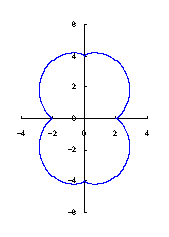
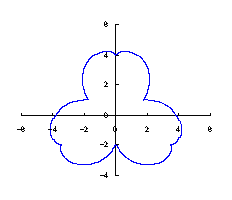
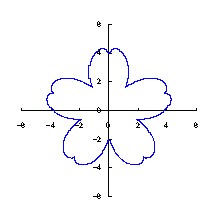
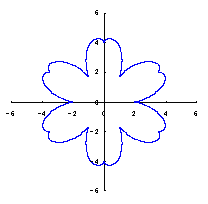
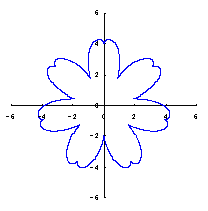
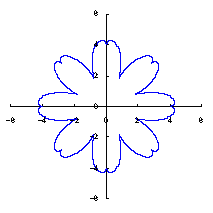
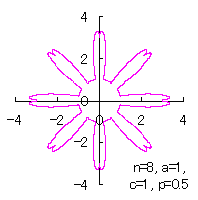
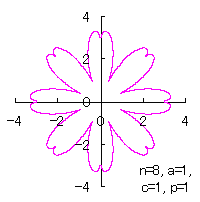
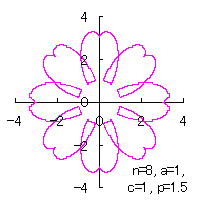
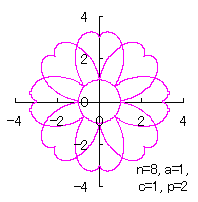
カージオイドから作り出す「ハート形曲線 II」の方法1で記述した元のカージオイドとそれから作り出されたハート形曲線の例を図1に示します。この形を土台となる中心円の周囲に周期的に配置して花の形を構成しようというものです。 |
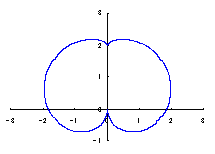 | 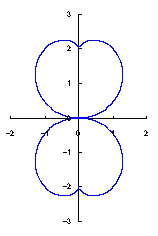 | 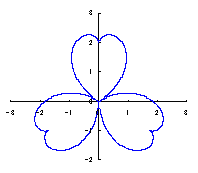 |  |
 |  |  |  |
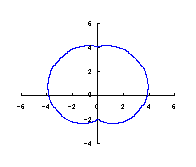 |  |  | 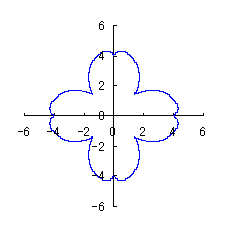 |
|
|
 |
 |
 |
 |
|
|
|
|
|
 |
 |
 |
 |
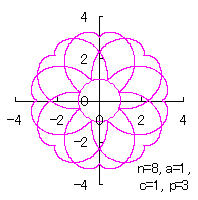 |
|
|
| 上図を着色しますと次のようです。
    
| |
| Sep. 21, 2012 に追記 | |
|
[2.1 の追記 II] 各花びらの位相角と土台となる中心円の位相角を独立にする場合
|
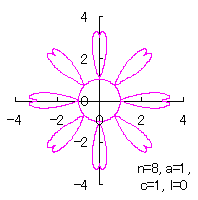 | 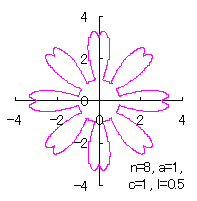 |
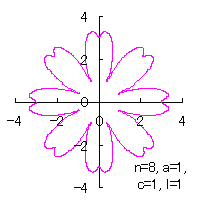 |
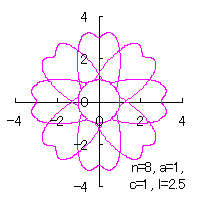 |
|
|
| |
| Sep. 30, 2012 に追記 | |
|
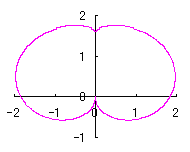
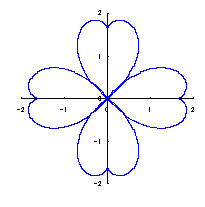
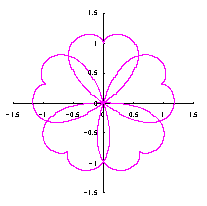
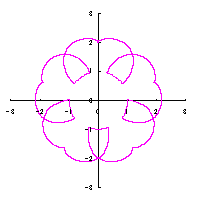
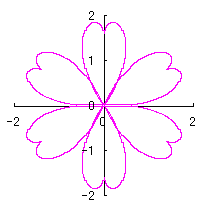
2.2 花弁となるハート形曲線の伸縮がある場合
|
 |
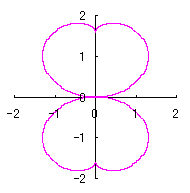 |
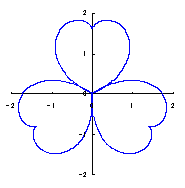 |
 |
|
|
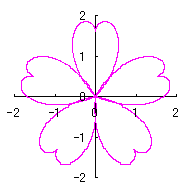 |
 |
 |
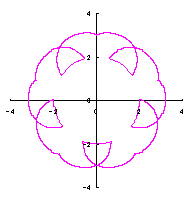 |
|
|
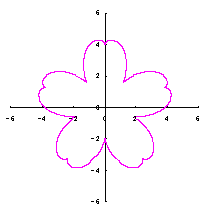 |
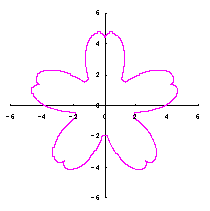 |
 |
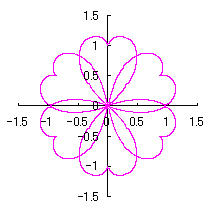 |
|
|
 |
 |
 |
 |
|
|
|
上図を着色しますと次のようです。クリックすると拡大の線画が現れます。
               
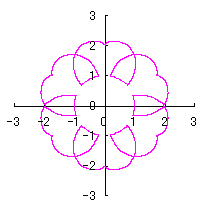
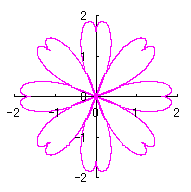
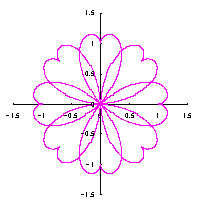
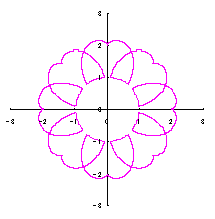
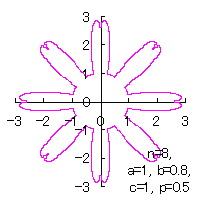
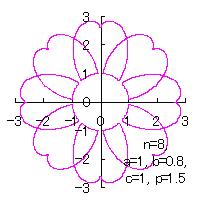
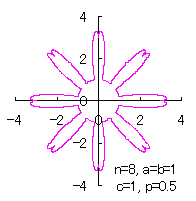
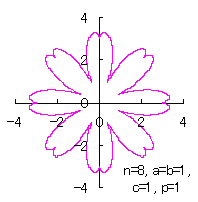
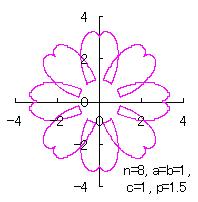
[2.2 の追記 I] 花びらを重ねる場合 1個の花びらの幅、すなわち、(11)式で与えられる角度 (8)式から(11)式、(13)式、(14)式、および、(B1)式を計算して得られた図形の例を図B1から図B8に示します。ただし、 |
 |
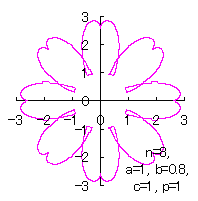 |  |
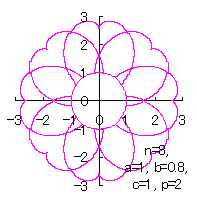 |
|
|
 |
 |
 |
 |
|
上図の前半部を着色しますと次のようです。




| |
| Sep. 21, 2012 に追記 | |
|
[2.2 の追記 II] 各花びらの位相角と土台となる中心円の位相角を独立にする場合
先ず、各花びらが土台となる中心円に1点で接する場合は、土台となる中心円の位相角は 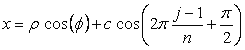 , (B2) , (B2)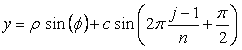 . (B3) . (B3)以上を拡張して、各花びらが土台となる中心円に任意の広がり幅で接する場合を説明します。 接する任意の広がり幅を、土台となる中心円の位相角で計って 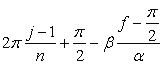 のように のように 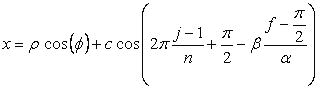 , (B4) , (B4)
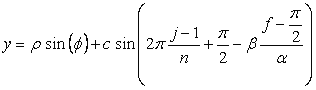 . (B5) . (B5)
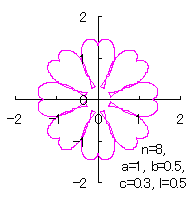
ここに、角度 (1)式から(3)式、および、(8)式から(12)式、(B4)式、および、(B5)式を計算して得られた図形の例を図B9から図B12に示します。ただし、 |
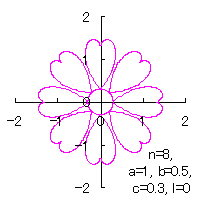 |
 |
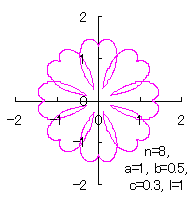 |
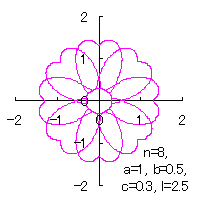 |
|
c=0.3, l=0 | c=0.3, l=0.5 | c=0.3, l=1 | c=0.3, l=2 |
| |
| Oct. 01, 2012 に追記 | |
|
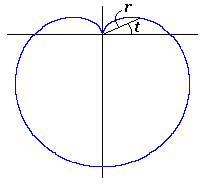
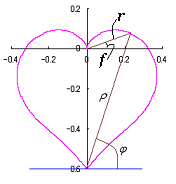
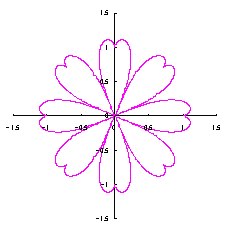
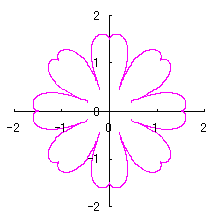
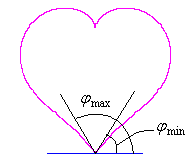
3. 方法2 方法2は、カージオイドの底に角度を形成するような位相角の変換式を適用して、花びらとなるハート形を作ることです。 3.1 花弁となるハート曲線を忠実に用いた場合 カージオイドから作り出す「ハート曲線 II」の方法2で作り出したハート曲線の1例を図31に示します。この形を円の周囲に周期的に配置して花の形を構成しようというものです。 |
 |  | 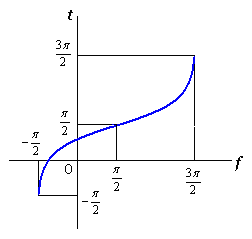 |
|
|
|
ハート曲線 IIの方法2で得られた式で、ここでも用いる式は次の(15)、(16)、および、(17)式です。
図31の原点をハート形の尖った底に移す必要があります。移動によって(16)式は変わりませんが、(17)式は次のように変更されます。
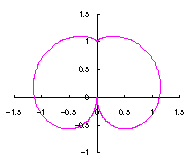
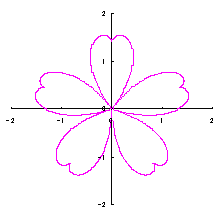
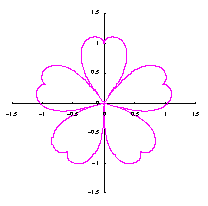
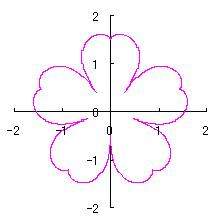
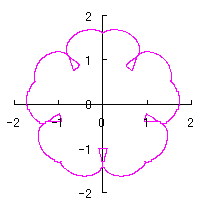
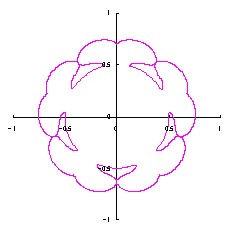
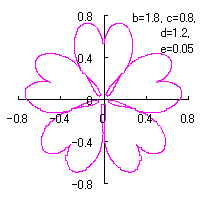
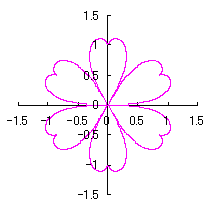
改めて、花の形を与える直交座標表示は次の2式になります。 |
 |
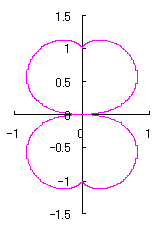 |
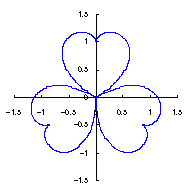 |
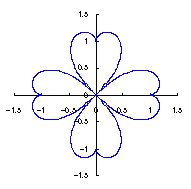 |
|
|
|
|
 |
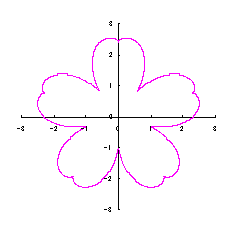 |
 |
 |
|
|
|
|
|
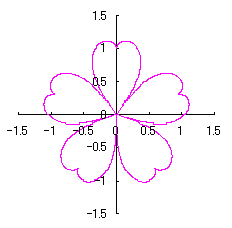 |
 |
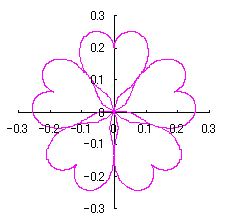 |
 |
|
|
|
|
|
 |
 |
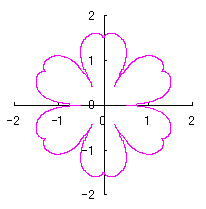 |
 |
 |
|
e=0.05 |
|
|
|
|
|
上図を着色しますと次のようです。クリックすると拡大の線画が現れます。
                
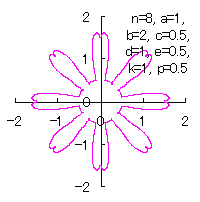
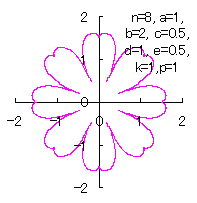
[3.1.1 の追記 I] 花びらを重ねる場合
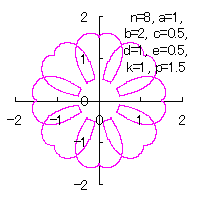
1個の花びらの幅を大きく取るとよい。このためには、図32の直線の傾きを大きくすると実現できます。この拡大率を |
 |
 |
 |
 |
|
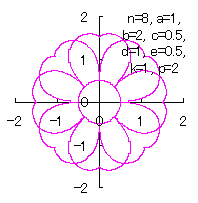
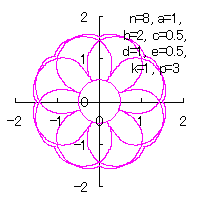
d=1, e=0.5, k=1, p=0.5 | d=1, e=0.5, k=1, p=1 | d=1, e=0.5, k=1, p=1.5 |
d=1, e=0.5, k=1, p=2 |
 |
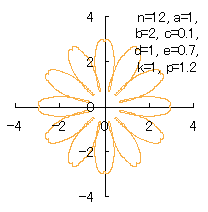 |
|
d=1, e=0.5, k=1, p=3 | d=1, e=0.7, k=1, p=1.2 |
上図を着色しますと次のようです。






| |
| Sep 22, 2012 に追記 | |
|
[3.1.1 の追記 II] 各花びらの位相角と土台となる中心円の位相角を独立にする場合 2.1 節の[2.1 の追記 II]や前節の[2.2 の追記 II]と同様に考えることができます。従って、[2.1 の追記 II]や[2.2 の追記 II]と同様に以下のように記述できます。
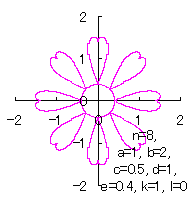
先ず、各花びらが土台となる中心円に1点で接する場合は、土台となる中心円の位相角は |
 |
 |
 |
 |
|
d=1, e=0.4, k=1, l=0 |
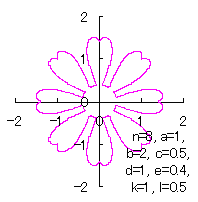
d=1, e=0.4, k=1, l=0.5 |
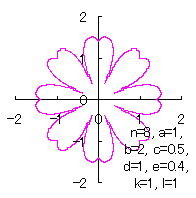
d=1, e=0.4, k=1, l=1 |
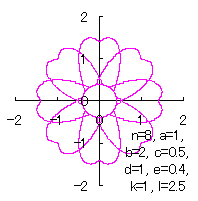
d=1, e=0.4, k=1, l=2.5 |
| |
| Oct. 01, 2012 に追記 | |
|
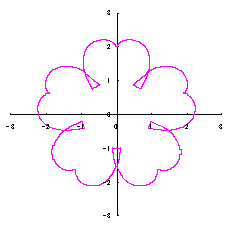
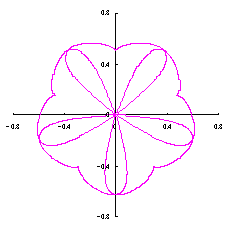
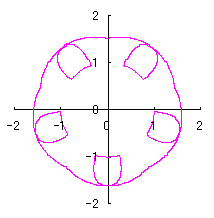
3.1.2 図34を用いた場合
|
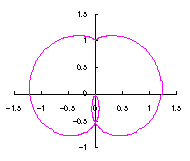 |
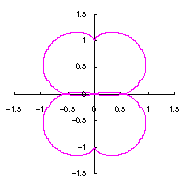 |
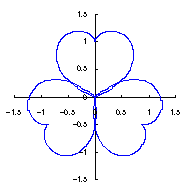 |
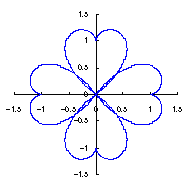 |
|
|
|
|
|
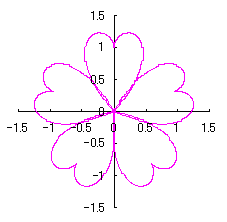 |
 |
 |
 |
|
|
|
|
|
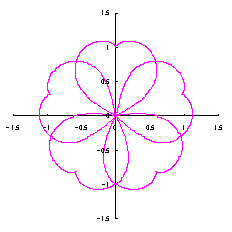 |
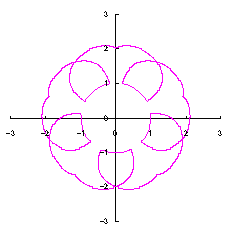 |
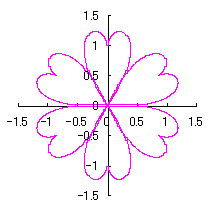 |
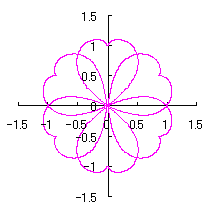 |
|
|
|
|
|
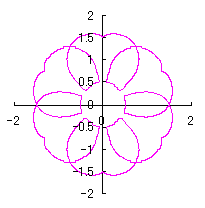 |
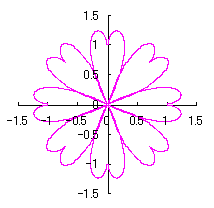 |
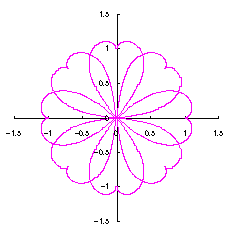 |
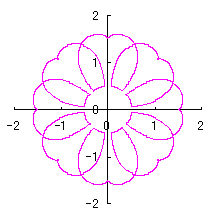 |
|
|
|
|
|
|
上図を着色しますと次のようです。クリックすると拡大の線画が現れます。
               
[3.1.2 の追記 I] 花びらを重ねる場合
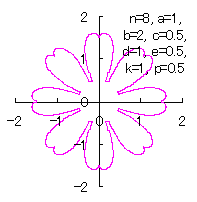
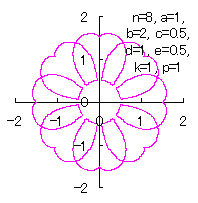
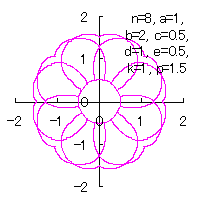
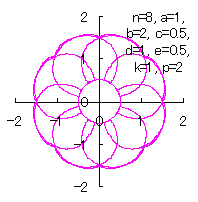
(15)式から(21)式、(23)式、(24)式、(CI1)式、(25)式、および、(26)式を計算して得られた図形の例を図CII1から図CII4に示します。ただし、 |
|
|
|
|
|
d=1, e=0.5, k=1, p=0.5 |
d=1, e=0.5, k=1, p=1 |
d=1, e=0.5, k=1, p=1.5 |
d=1, e=0.5, k=1, p=2 |
|
上図を着色しますと次のようです。    
| |
| Sep 22, 2012 に追記 | |
|
[3.1.2 の追記 II] 各花びらの位相角と土台となる中心円の位相角を独立にする場合 2.1 節の[2.1 の追記 II]や2.2 節の[2.2 の追記 II]、および、前節の[3.1.1 の追記 II]と同様に考えることができます。従って、[2.1 の追記 II]や[2.2 の追記 II]、および、[3.1.1 の追記 II]と同様に以下のように記述できます。 先ず、各花びらが土台となる中心円に1点で接する場合は、土台となる中心円の位相角は 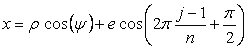 , (CII1) , (CII1)
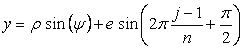 . (CII2) . (CII2)
以上を拡張して、各花びらが土台となる中心円に任意の広がり幅で接する場合を説明します。 接する任意の広がり幅を、土台となる中心円の位相角で計って 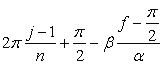 のように のように 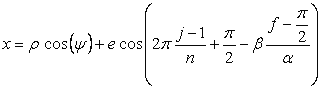 , (CII3) , (CII3)
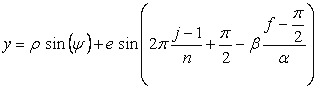 . (CII4) . (CII4)
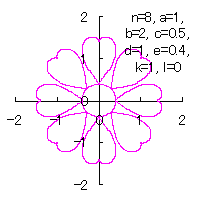
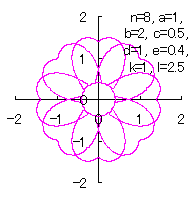
ここに、角度 (15)式から(22)式、(25)式、(26)式、(CII3)式、および、(CII4)式を計算して得られた図形の例を図CII5から図CII8に示します。ただし、 |
 |
 |
 |
 |
|
d=1, e=0.4, k=1, l=0 |
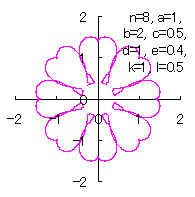
d=1, e=0.4, k=1, l=0.5 |
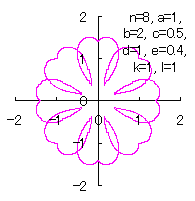
d=1, e=0.4, k=1, l=1 |
d=1, e=0.4, k=1, l=2.5 |
| |
| Oct. 01, 2012 に追記 | |
|
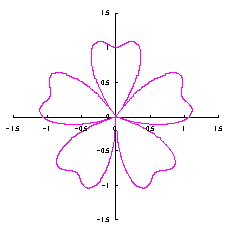
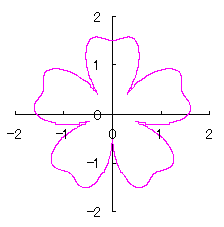
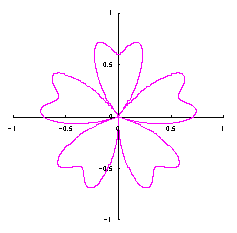
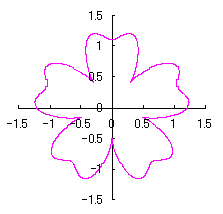
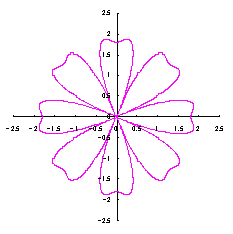
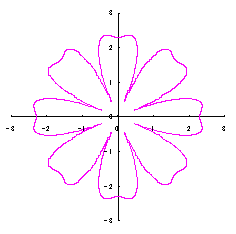
3.2 花弁となるハート曲線を簡略化した場合
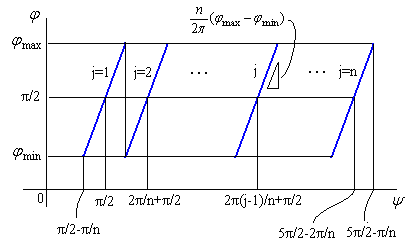
前節3.1はハート形の正確な形を保持するために、プロセスが込み入っています。そこで、前節の(22)式、および、図32の正確な位相角 |
 |
 |
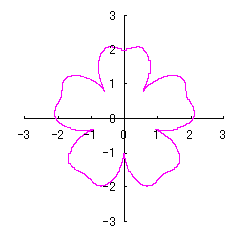 |
 |
|
|
|
|
|
 |
 |
 |
|
|
|
|
|
上図を着色しますと次のようです。クリックすると拡大の線画が現れます。
      
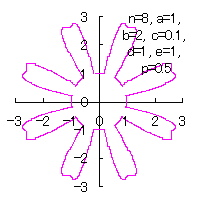
[3.2 の追記 I] 花びらを重ねる場合
3.1 節前半の(15)式から(20)式、および、上記の(27)式、(28a)式、および、(28b)式がそのまま使えます。 |
 |
 |
 |
 |
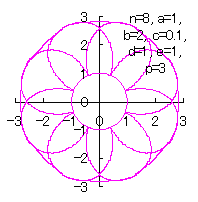 |
|
c=0.1, d=1, e=1, p=0.5 |
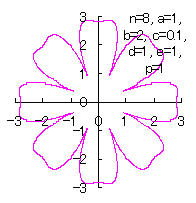
c=0.1, d=1, e=1, p=1 |
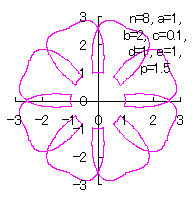
c=0.1, d=1, e=1, p=1.5 |
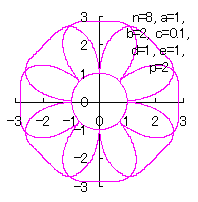
c=0.1, d=1, e=1, p=2 |
c=0.1, d=1, e=1, p=3 |
|
上図を着色しますと次のようです。





| |
| Sep 22, 2012 に追記 | |
|
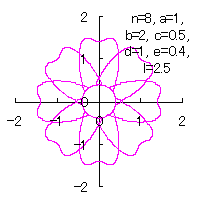
[3.2 の追記 II] 各花びらの位相角と土台となる中心円の位相角を独立にする場合 3.1
節前半の(15)式から(22)式、および、上記の(27)式がそのまま使えます。2.1 節の[2.1 の追記 II]や2.2 節の[2.2 の追記 II]、および、前節の[3.1.1 の追記 II]と同様に考えることができます。従って、[2.1 の追記 II]や[2.2 の追記 II]、および、[3.1.1 の追記 II]と同様に以下のように記述できます。 |
 |
 |
 |
 |
|
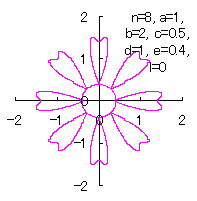
c=0.5, d=1, e=0.4, l=0 |
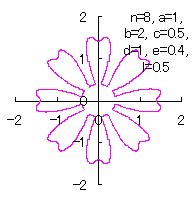
c=0.5, d=1, e=0.4, l=0.5 |
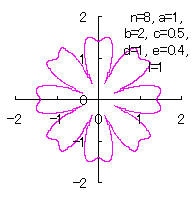
c=0.5, d=1, e=0.4, l=1 |
c=0.5, d=1, e=0.4, l=2.5 |
| |
| Oct. 02, 2012 に追記 | |
|
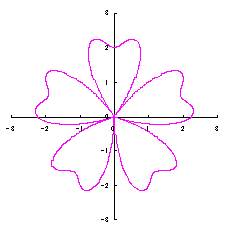
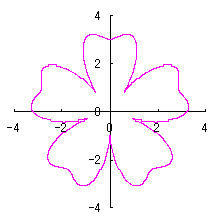
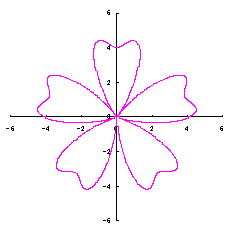
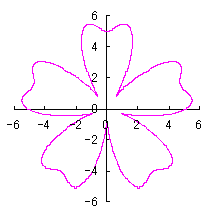
4. カージオイドをそのままに花びらに用いる場合
ここでは単純にカージオイドをそのまま花びらに用いる場合を扱います。
|
 |
 |
 |
 |
|
|
|
|
|
|
上図を着色しますと次のようです。クリックすると拡大の線画が現れます。
   
4.2 花びらの重なりがある場合 各花びらが交互に重なり合う場合は、元の1個のカージオイドの位相 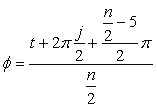 , (35-1) , (35-1)
ただし、 さらに、重なり合いを示す指標を 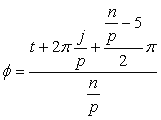 , (35-2) , (35-2)
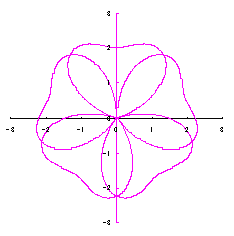
ただし、 (18)式、および、(29)式から(33)式、および、(35-1)式、または、(35-2)式をコンピュータで計算して得た花の形の例を以下に示します。ただし、 |
 |
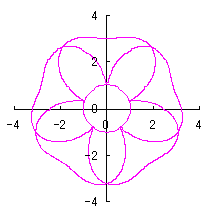 |
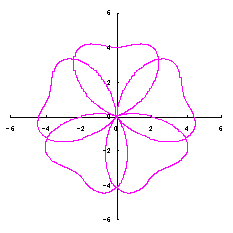 |
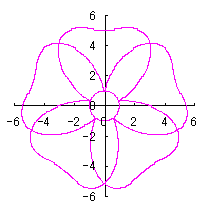 |
|
|
|
|
|
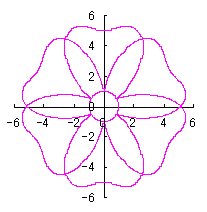 |
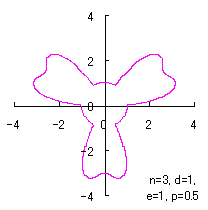 |
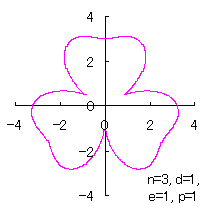 |
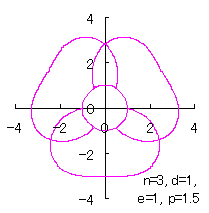 |
|
|
|
|
|
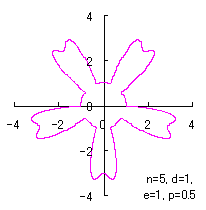 |
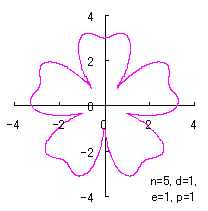 |
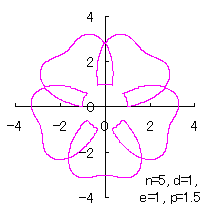 |
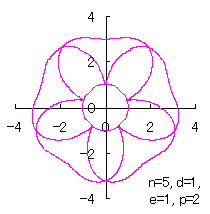 |
|
|
|
|
|
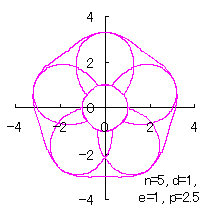 |
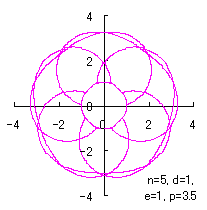 |
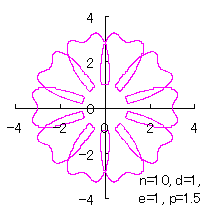 |
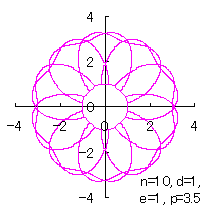 |
|
|
|
|
|
|
上図を着色しますと次のようです。クリックすると線画が現れます。
               
| |
| edited in Mar. 11, 2009 & reviced in Sep. 11, 2012 | |
|
4.3 各花びらの位相角と土台となる中心円の位相角を独立にする場合 前節までの(18)式、および、(29)式から(33)式がそのまま使えます。さらに、3.2 節の[3.2 の追記 II]と同様に考えることができ、[3.2 の追記 II]の(D3)、(D4)式が使えます。なお、C プログラムでは、補正係数 (18)式、(29)式から(33)式、(D3)式、および、(D4)式を計算して得られた図形の例を図E1から図E4に示します。ただし、 |
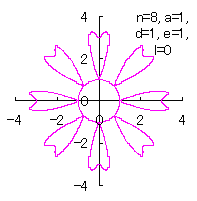 |
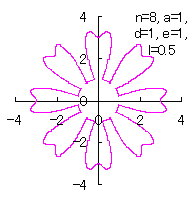 |
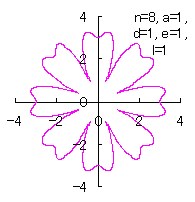 |
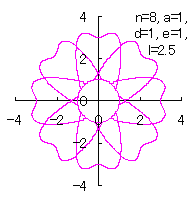 |
|
|
|
|
|
| |
| Oct. 02, 2012 に追記 | |
|
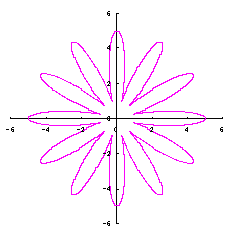
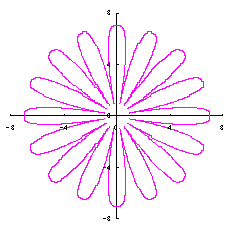
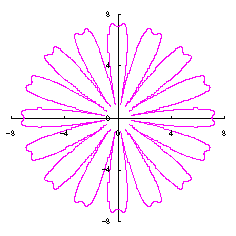
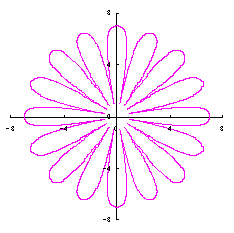
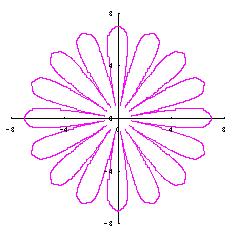
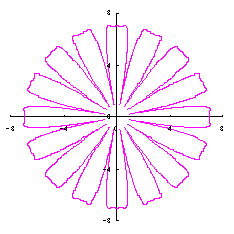
5. 円をそのままに花びらに用いる場合(その1)
ここでは単純に円をそのまま花びらに用いる場合を扱います。
|
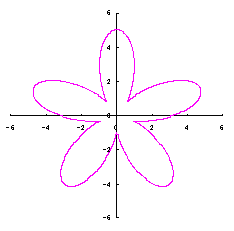 |
 |
 |
 |
|
|
|
 |
 |
 |
|
|
|
|
上図を着色しますと次のようです。クリックすると拡大の線画が現れます。
      
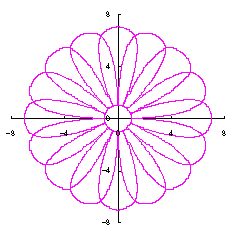
5.1.2 花びらの重なりがある場合 この場合、元の1個の円の位相 (31)式から(33)式、(35)式または(35-2)式、(36)、および、(37)式をコンピュータで計算して得た花の形の例を以下に示します。ただし、 |
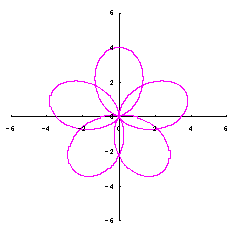 |
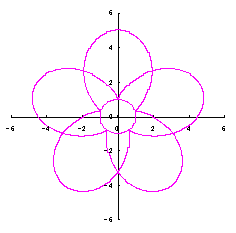 |
 |
 |
|
d=2, e=0, p=2 |
d=2, e=1, p=2 |
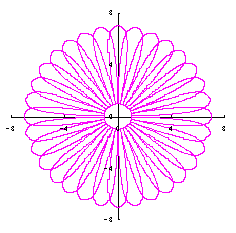
d=3, e=1, p=2 |
d=3, e=1, p=2 |
 |
 |
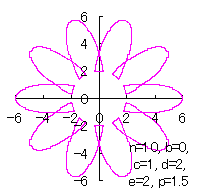 |
 |
|
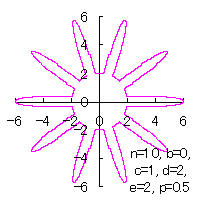
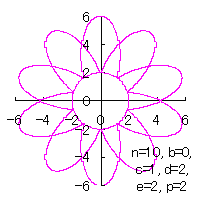
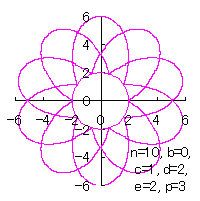
d=2, e=2, p=0.5 |
d=2, e=2, p=1 |
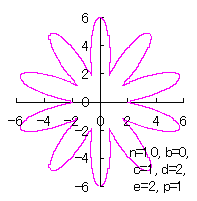
d=2, e=2, p=1.5 |
d=2, e=2, p=2 |
 |
 |
|
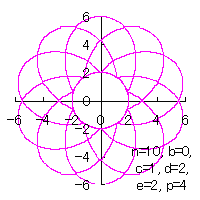
d=2, e=2, p=3 |
d=2, e=2, p=4 |
|
上図のうち、図83から図85b、および、図86fを着色しますと次のようです。最初の4つの図はクリックすると拡大の線画が現れます。
    
| |
| edited in Mar. 11, 2009 & reviced in Sep. 14, 2012 | |
|
5.1.3 各花びらの位相角と土台となる中心円の位相角を独立にする場合 前節までの(27)式、および、(31)式、(36)式、(37)式がそのまま使えます。さらに、3.2 節の[3.2 の追記 II]と同様に考えることができ、[3.2 の追記 II]の(D3)、(D4)式が使えます。なお、C プログラムでは、補正係数 (27)式、(31)式、(36)式、(37)式、(D3)式、および、(D4)式を計算して得られた図形の例を図F1aから図F1dに示します。ただし、 |
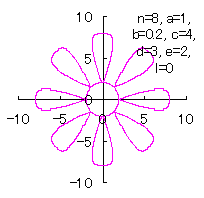 |
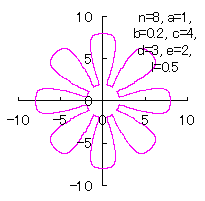 |
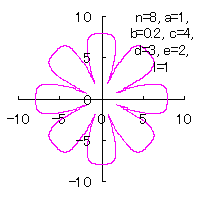 |
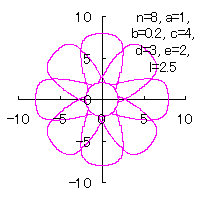 |
|
d=3, e=2, l=0 |
d=3, e=2, l=0.5 |
d=3, e=2, l=1 |
d=3, e=2, l=2.5 |
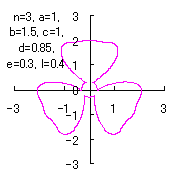 |
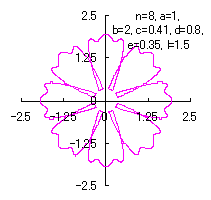 |
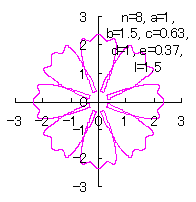 |
|
d=0.85, e=0.3, l=0.4 |
d=0.8, e=0.35, l=1.5 |
d=1, e=0.37, l=1.5 |
|
上図のうち、図F1f と図F1g を着色しますと次のようです。クリックすると拡大の線画が現れます。
 
| |
| Oct. 02, 2012 に追記 | |
|
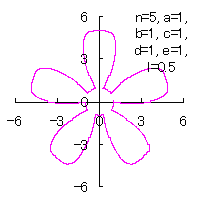
5.1.4 (36)式と(37)式の符号を変更して 5.1.3 節の計算プログラムに従う場合 (36)式と(37)式の符号を変更して計算プログラムは5.1.3節に従う場合を、符号の変更の仕方で7通りに分けて扱います。 5.1.4 (i) その1 (36)式と(37)式に代えて、次式を想定します。 ここに、(E2)式の最後の項は原点を変形された円の底に移動させるためのものです。 (E1)式、(E2)式、(31)式、(27)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
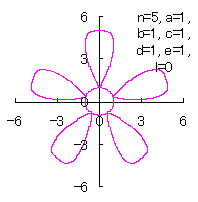 |
 |
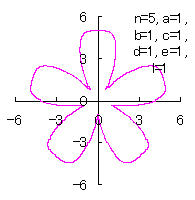 |
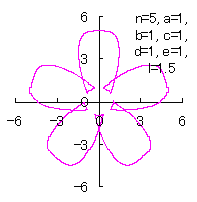 |
|
d=1, e=1, l=0 |
d=1, e=1, l=0.5 |
d=1, e=1, l=1 |
d=1, e=1, l=1.5 |
| |
| Oct. 16, 2012 に追記 | |
|
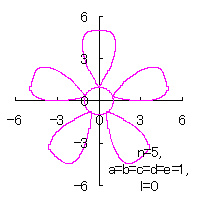
5.1.4 (ii) その2
(36)式と(37)式に代えて、次式を想定します。 |
 |
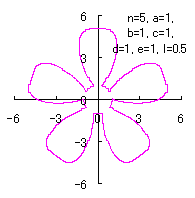 |
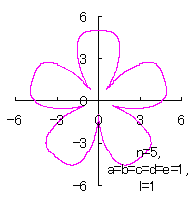 |
|
d=1, e=1, l=0 |
d=1, e=1, l=0.5 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
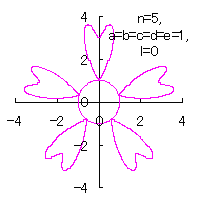
5.1.4 (iii) その3 (36)式と(37)式に代えて、次式を想定します。 ここに、(E6)式の最後の項は原点を変形された円の底に移動させるためのものです。 (E5)式、(E6)式、(31)式、(27)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
 |
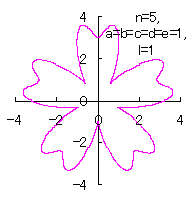 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
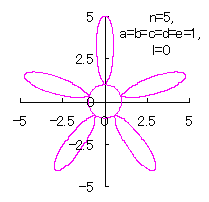
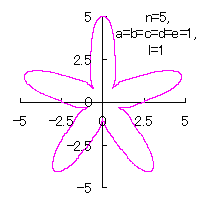
5.1.4 (iv) その4 (36)式と(37)式に代えて、次式を想定します。 ここに、(E8)式の最後の項は原点を変形された円の底に移動させるためのものです。 (E7)式、(E8)式、(31)式、(27)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
 |
 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
5.1.4 (v) その5 (36)式と(37)式に代えて、次式を想定します。 ここに、(E10)式の最後の項は原点を変形された円の底に移動させるためのものです。 (E9)式、(E10)式、(31)式、(27)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
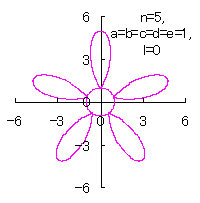 |
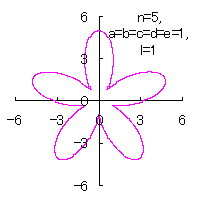 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
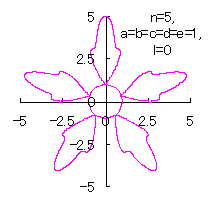
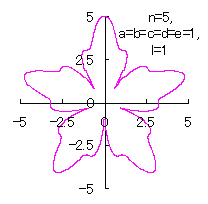
5.1.4 (vi) その6 (36)式と(37)式に代えて、次式を想定します。 ここに、(E12)式の最後の項は原点を変形された円の底に移動させるためのものです。 (E11)式、(E12)式、(31)式、(27)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
 |
 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
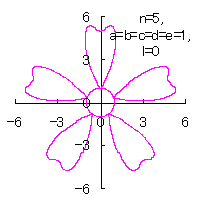
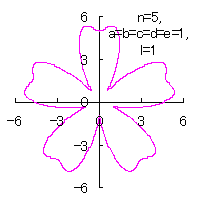
5.1.4 (vii) その7 (36)式と(37)式に代えて、次式を想定します。 ここに、(E14)式の最後の項は原点を変形された円の底に移動させるためのものです。 (E13)式、(E14)式、(31)式、(27)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
 |
 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
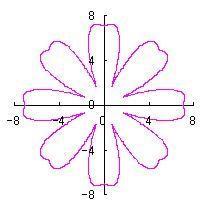
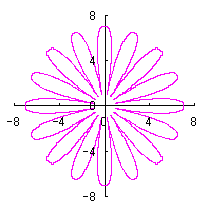
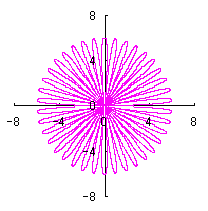
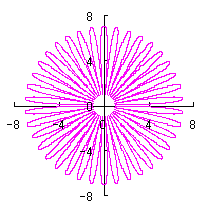
5.2 変形された円の想定2
変形された円を表す式を、直交座標表示で次のようにしました。
5.2.1 花びらの重なりがない場合
5.1節と同様、元の1個の円の位相 |
 |
 |
 |
 |
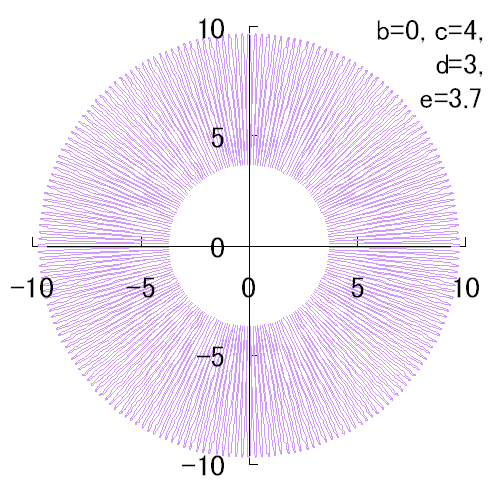 |
|
|
|
|
|
|
|
上図を着色しますと次のようです。クリックすると拡大の線画が現れます。
    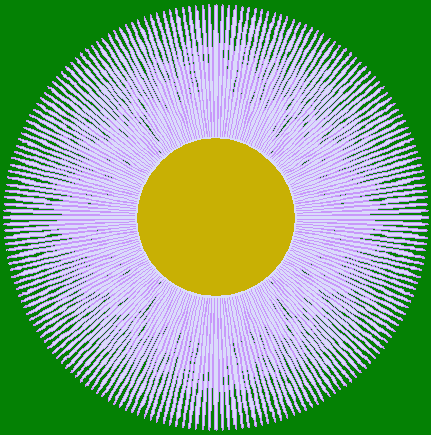
| |
| A part of the figures and the picture are added in May 14, 2013. | |
|
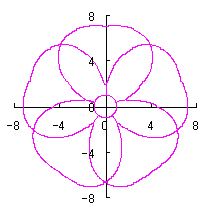
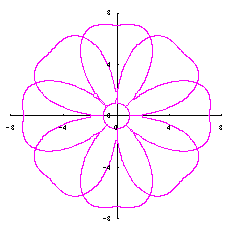
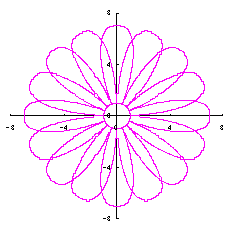
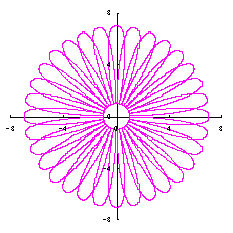
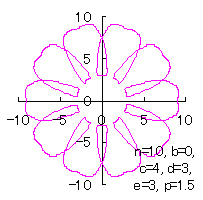
5.2.2 花びらの重なりがある場合
5.1節と同様、元の1個の円の位相 |
 |
 |
 |
 |
|
d=3, e=1, p=2 |
d=3, e=1, p-2 |
d=3, e=1, p=2 |
d=3, e=1, p=2< |
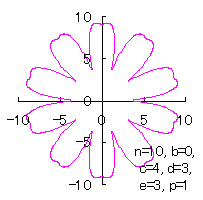
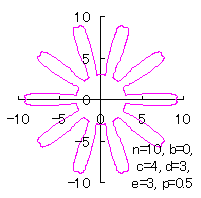 |
 |
 |
 |
|
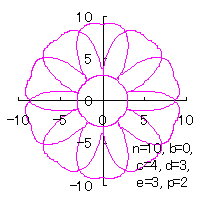
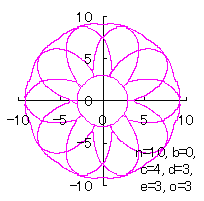
d=3, e=3, p=0.5 |
d=3, e=3, p=1 |
d=3, e=3, p=1.5 |
d=3, e=3, p=2 |
 |
 |
|
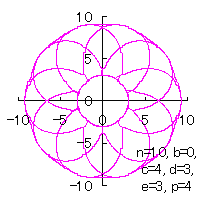
d=3, e=3, p=3 |
d=3, e=3, p=4 |
|
上図のうち図89から図91b、および、図92fを着色しますと次のようです。中4つの図はクリックすると拡大の線画が現れます。
     
| |
| edited in Mar. 11, 2009 & reviced in Sep. 15, 2012 | |
|
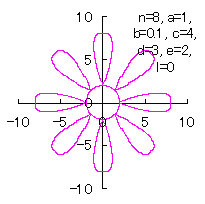
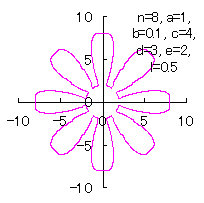
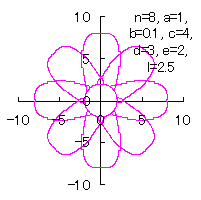
5.2.3 各花びらの位相角と土台となる中心円の位相角を独立にする場合
|
 |
 |
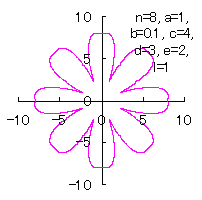 |
 |
|
d=3, e=2, l=0 |
d=3, e=2, l=0.5 |
d=3, e=2, l=1 | d=3, e=2, l=2.5 |
| |
| Oct. 02, 2012 に追記 | |
|
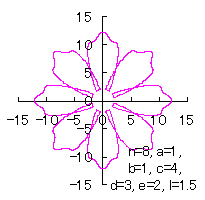
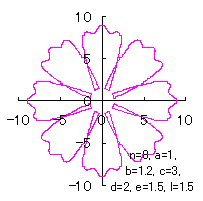
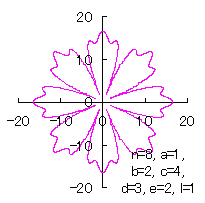
5.2.4 (38)式と(39)式の符号を変更して 5.2.3 節の計算プログラムに従う場合
|
 |
 |
 |
|
d=3, e=2, l=1.5 | d=2, e=1.5, l=1.5 |
d=3, e=2, l=1 |
|
上図のうち図F2f を着色しますと次のようです。クリックすると拡大の線画が現れます。

| |
| Oct. 09, 2012 に追記 | |
|
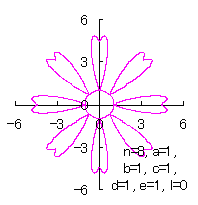
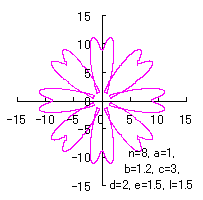
5.2.4 (ii) その2
(38)式と(39)式に代えて、次式を想定します。 |
 |
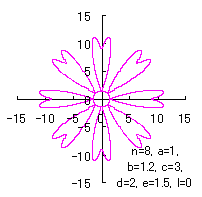 |
 |
|
d=1, e=1, l=0 |
d=2, e=1.5, l=0 |
d=2, e=1.5, l=1.5 |
| |
| Oct. 09, 2012 に追記 | |
|
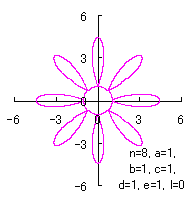
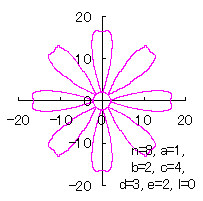
5.2.4 (iii) その3
(38)式と(39)式に代えて、次式を想定します。 |
 |
 |
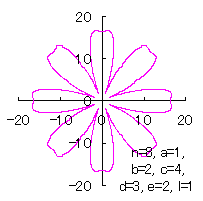 |
|
d=1, e=1, l=0 |
d=3, e=2, l=0 |
d=3, e=2, l=1 |
| |
| Oct. 09, 2012 に追記 | |
|
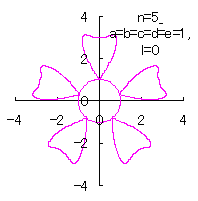
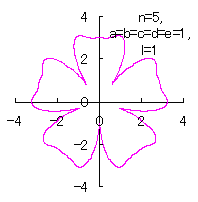
5.2.4 (iv) その4
(38)式と(39)式に代えて、次式を想定します。 |
 |
 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
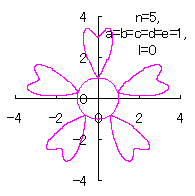
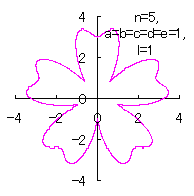
5.2.4 (v) その5
|
 |
 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
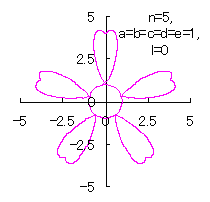
5.2.4 (vi) その6
(38)式と(39)式に代えて、次式を想定します。 |
 |
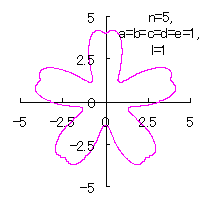 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
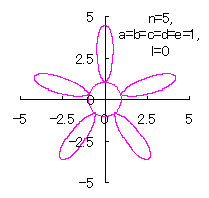
5.2.4 (vii) その7
|
 |
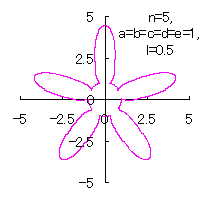 |
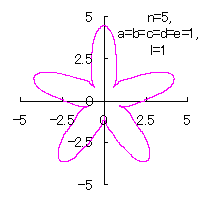 |
|
d=1, e=1, l=0 |
d=1, e=1, l=0.5 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
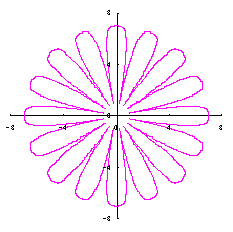
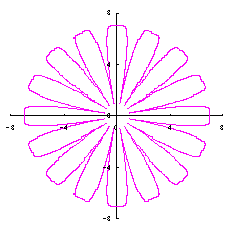
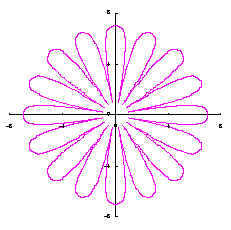
5.3 変形された円の想定3
変形された円を表す式を、直交座標表示で次のようにしました。 |
 |
 |
 |
|
|
|
|
|
上図を着色しますと次のようです。クリックすると拡大の線画が現れます。
  
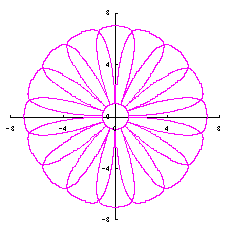
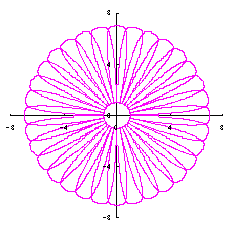
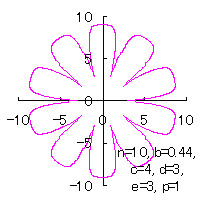
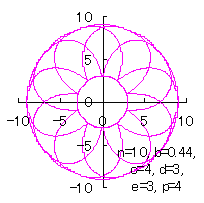
5.3.2 花びらの重なりがある場合 5.1節、および、5.2節と同様、元の1個の円の位相 (31)式から(33)式、および、(35-1)式または(35-2)式、(40)、(41)式をコンピュータで計算して得た花の形の例を以下に示します。ただし、 |
 |
 |
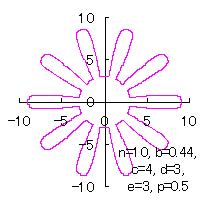 |
 |
|
c=4, d=3, e=1, p=2 |
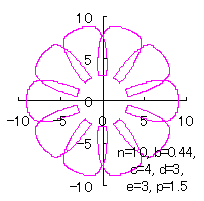
c=4, d=3, e=1, p=2 |
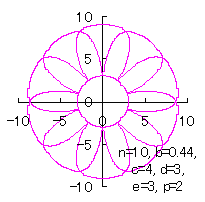
c=4, d=3, e=3, p=0.5 |
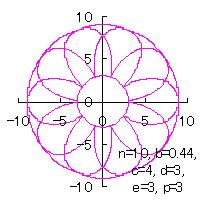
c=4, d=3, e=3, p=1 |
 |
 |
 |
 |
|
c=4, d=3, e=3, p=1.5 |
c=4, d=3, e=3, p=2 |
c=4, d=3, e=3, p=3 |
c=4, d=3, e=3, p=4 |
|
上図のうち図96a と b、および、図97fを着色しますと次のようです。最初の2つの図はクリックすると拡大の線画が現れます。
  
| |
| edited in Mar. 11, 2009 & reviced in Sep. 16, 2012 | |
|
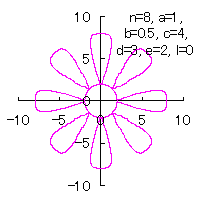
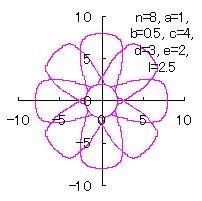
5.3.3 各花びらの位相角と土台となる中心円の位相角を独立にする場合
|
 |
 |
 |
 |
|
d=3, e=2, l=0 |
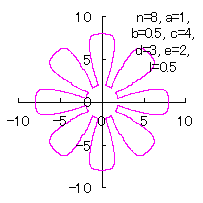
d=3, e=2, l=0.5 |
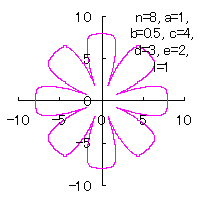
d=3, e=2, l=1 |
d=3, e=2, l=2.5 |
| |
| Oct. 02, 2012 に追記 | |
|
5.3.4 (38)式と(39)式の符号を変更して 5.3.3 節の計算プログラムに従う場合 (40)式と(41)式の符号を変更して計算プログラムは5.3.3節に従う場合を、符号の変更の仕方で7通りに分けて扱います。 5.3.4 (i) その1 (40)式と(41)式に代えて、次式を想定します。 ここに、(G2)式の最後の項は原点を変形された円の底に移動させるためのものです。 (27)式、(31)式、(G1)式、(G2)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
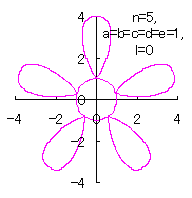 |
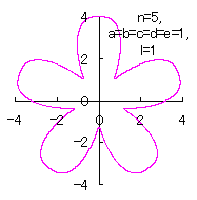 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
5.3.4 (ii) その2 (40)式と(41)式に代えて、次式を想定します。 ここに、(G4)式の最後の項は原点を変形された円の底に移動させるためのものです。 (27)式、(31)式、(G3)式、(G4)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
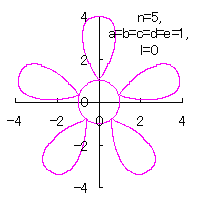 |
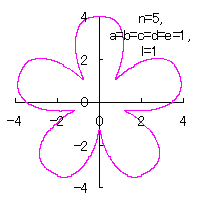 |
|
d=3, e=2, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
5.3.4 (iii) その3 (40)式と(41)式に代えて、次式を想定します。 ここに、(G6)式の最後の項は原点を変形された円の底に移動させるためのものです。 (27)式、(31)式、(G5)式、(G6)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
 |
 |
|
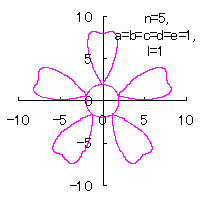
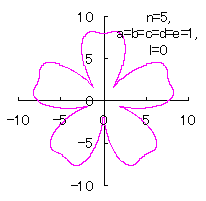
d=3, e=2, l=0 | d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
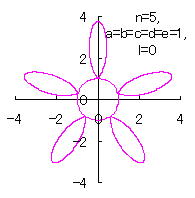
5.3.4 (iv) その4 (40)式と(41)式に代えて、次式を想定します。 ここに、(G8)式の最後の項は原点を変形された円の底に移動させるためのものです。 (27)式、(31)式、(G7)式、(G8)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
 |
 |
|
d=3, e=2, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
5.3.4 (v) その5
(40)式と(41)式に代えて、次式を想定します。 |
 |
 |
|
d=3, e=2, l=0 |
d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
5.3.4 (vi) その6 (40)式と(41)式に代えて、次式を想定します。 ここに、(G12)式の最後の項は原点を変形された円の底に移動させるためのものです。 (27)式、(31)式、(G11)式、(G12)式、(D3)式、および、(D4)式を計算して得られた図形の例を以下に示します。 |
 |
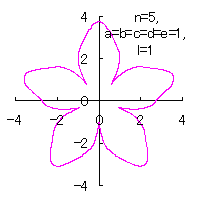 |
|
d=3, e=2, l=0 | d=1, e=1, l=1 |
| |
| Oct. 16, 2012 に追記 | |
|
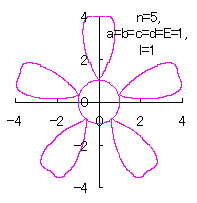
5.3.4 (vii) その7
(40)式と(41)式に代えて、次式を想定します。 |
 |
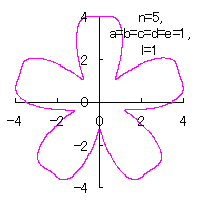 |
|
d=3, e=2, l=0 |
d=1, e=1, l=1 |
| |||||||||||
| Oct. 16, 2012 に追記 | |||||||||||
|
6. 各花びらの位相角と中心円の位相角を独立に設定して描く方法 前節までは、各花びらとその土台となる中心円の位相角を共通にして花を構成してきた。このやり方では、土台となる中心円の決められた角度領域を越えて花びらの横幅を広げることができません。 そこで、花びらの構成は上記通りですが、原点に立ち返って、最初からその設計をやり直し、各花びらの位相角と中心円の位相角を独立に設定して花を描くことを試みます。先ず、円形をもとに花びらを構成することから始め、余裕があれば、ハート形から花びらを構成することも試みますが、後者については行わないかもしれません。
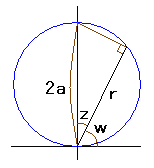
次に、「ハート曲線 II」の 2 節の「方法1」 や上記 2.1 節で記述したのと同じように、花びらの底が与えられた角度 6.1.1 各花びらの位相角と土台となる中心円の位相角を共通にする前節までと同じ場合(比較のための参考)
6.1.2 各花びらの位相角と土台となる中心円の位相角を独立にする場合 各花びらのが土台となる中心円とどのように接するか、などで、以下の3つの場合に分けました。 6.1.2 (i) 各花びらが土台となる中心円に1点で接する場合 この場合は、土台となる中心円の位相角は 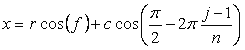 , (52) , (52)
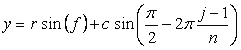 . (53) . (53)
(42)式、(48)または(48b)式、(49)式、(52)式、および、(53)式を計算することにより、花の形の (x, y) 座標が求められます。こうして得られた図形の例を図101に示します。ただし、
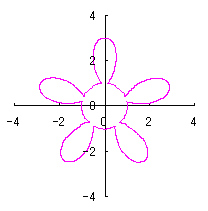
6.1.2 (ii) 各花びらが土台となる中心円に任意の広がり幅で接する場合
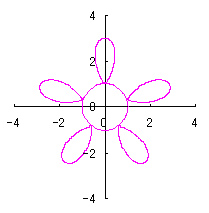
接する任意の広がり幅を土台となる中心円の位相角で計って |
 |
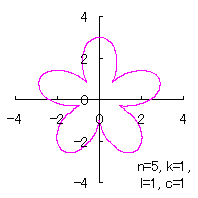 |
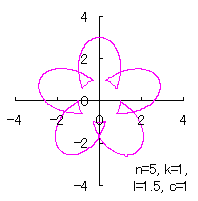 |
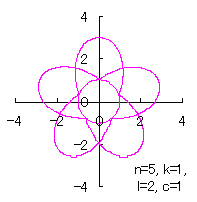 |
|
|
|
|
|
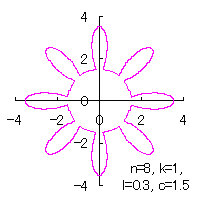 |
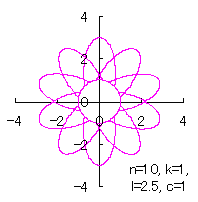 |
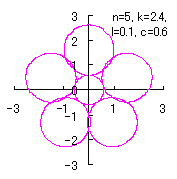 |
|
|
|
|
|
|
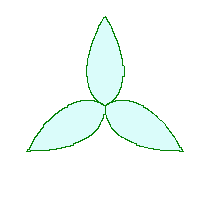
6.1.2 (iii) 前項 6.1.2 (ii) において花びらの先を尖らせる場合(その1) 前項 6.1.2 (ii) において、一例として(42)式を次式に変更するだけでよく、他の式は前項と同じです。 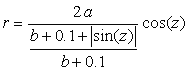 , (56-1) , (56-1)
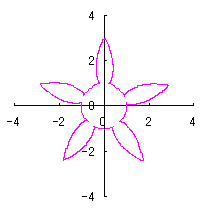
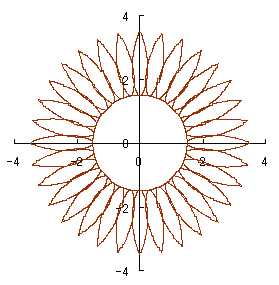
(56)式、(48)または(48b)式、(49)式、(54)式、および、(55)式を計算することにより、花の形の (x, y) 座標が求められます。こうして得られた図形の例を図103aから図103dに示します。ただし、 |
| (クリックすると拡大の線画が現れます) | |||
 |
 |
 |
|
|
|
|
| (クリックすると拡大の線画が現れます) | |||
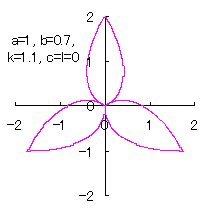 |
 |
|
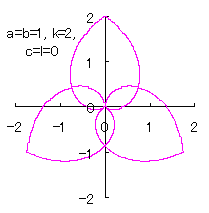 |
|
|
|
| |
| July 09, 2012 & Sep 09, 2012 | |
|
6.1.2 (iv) 前項 6.1.2 (ii) において花びらの先を尖らせる場合(その2)
前項 6.1.2 (iii) の(56-1)式を次式に変えてみます。 |
|
(クリックすると 拡大の線画が現れます) | ||
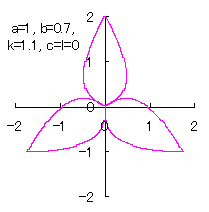 |
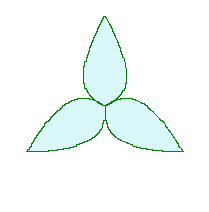 |
|
|
|
| |||||||
| Sep 09, 2012 | |||||||
|
6.2 カージオイドから花びらを構成する場合 カージオイドから花びらの形の基本となるハート形への変換は、第2節の方法1と第3節の方法2がありました。以下にその2通りを扱います。 6.2.1 第2節の方法1に従う場合
ここでは前述の「第2節 方法1」に添って行います。第2節と異なるのは、花びらと中心円の位相を互いに独立に設定することです。よって、最初の記述は第2節と重複もありますが、分かりやすくするために再録します。
次に、カージオイドの底が、ハート形に移行するハートの底の与えられた角度
一方、1個の花びらが中心円と接する角度範囲を中心円の位相角で計って 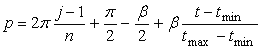 , (68) , (68)
ここに、 以上より、全体の花の形の (x, y)座標は、(54)および(55)式と同様に次の2式で得られます。 以上、(57)式から(70)式を用いて計算することにより、花の形の (x, y)座標が求められます。こうして得られた図形の例を以下に示します。ただし、 |
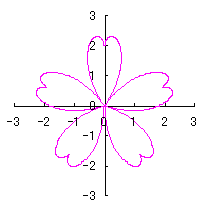 |
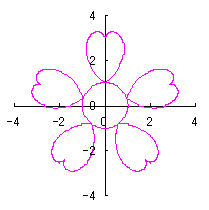 |
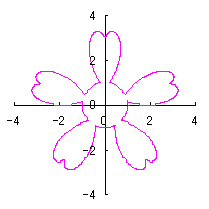 |
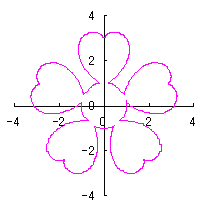 |
|
|
|
|
|
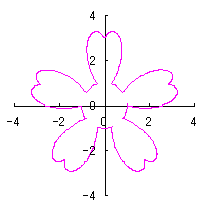 |
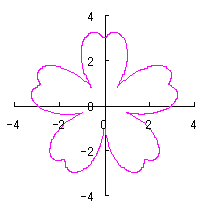 |
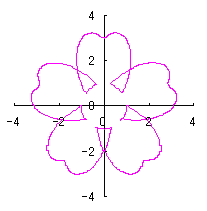 |
|
|
|
|
| |
| July 14, 2012 | |
|
6.2.2 第2節の方法2に従う場合
ここでは前述の「第3節 方法2」に添って行います。第2節と異なるのは、花びらと中心円の位相を互いに独立に設定することです。よって、最初の記述は第2節と重複もありますが、分かりやすくするために再録します。
|
 |
 |
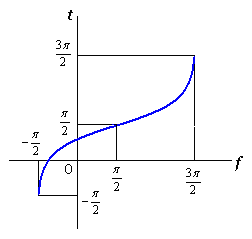 |
|
|
|
|
|
こうして、カージオイドの底に角度をなすように変換できます。
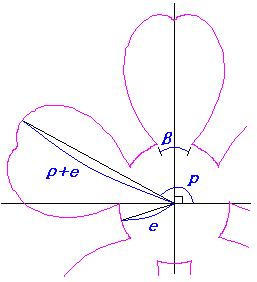
一方、1個の花びらが中心円と接する角度範囲を中心円の位相角で計って 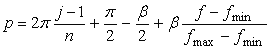 , (78) , (78)
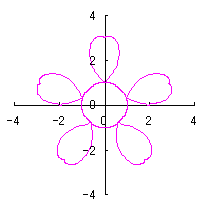
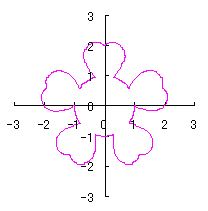
ここに、 以上より、全体の花の形の (x, y)座標は、(69)および(70)式と同様に次の2式で得られます。 以上、(71)式から(80)式を用いて計算することにより、花の形の (x, y)座標が求められます。こうして得られた図形の例を以下に示します。ただし、 |
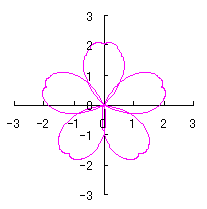 |
 |
 |
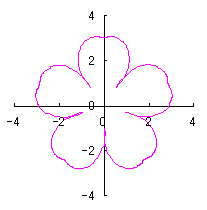 |
|
d=1, e=0, k=1, l=0 |
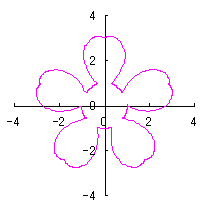
d=1, e=1, k=1, l=0 |
d=1, e=1, k=1, l=0.5 |
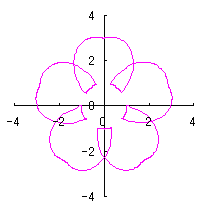
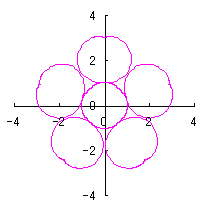
d=1, e=1, k=1, l=1 |
 |
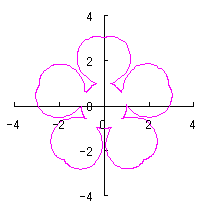 |
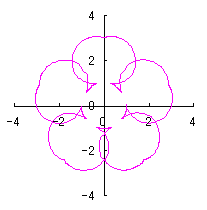 |
 |
|
d=1, e=1, k=1, l=1.5 |
d=1, e=1, k=1.5, l=0.5 |
d=1, e=1, k=2, l=0.5 |
d=1, e=1, k=2, l=0 |
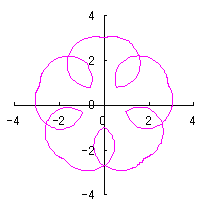 |
 |
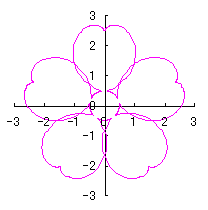 |
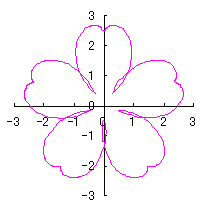 |
|
d=1, e=1, k=2, l=1 |
d=1, e=1, k=2, l=0.5 |
d=1, e=0.5, k=1, l=0.3 |
d=1, e=0.5, k=0.7, l=1 |
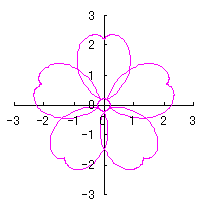 |
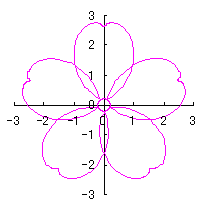 |
 |
 |
|
d=1, e=0.2, k=0.8, l=1 |
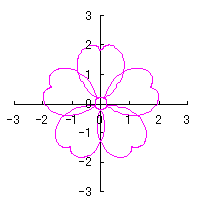
d=1, e=0.2, k=0.8, l=1 |
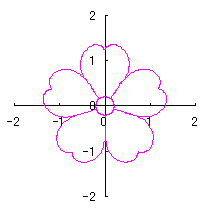
d=1, e=0.2, k=0.8, l=1 |
d=1, e=0.2, k=1.5, l=1 |
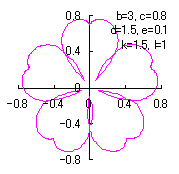 |
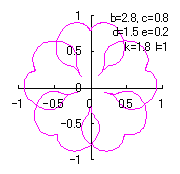 |
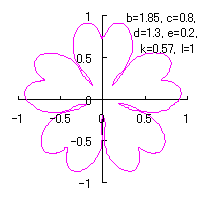 |
|
d=1.5, e=0.1, k=1.5, l=1 |
d=1.5, e=0.2, k=1.8, l=1 |
d=1.5, e=0.2, k=0.6, l=1 |
|
図127、図128、および、図132d を着色しますと次のようです。クリックすると拡大の線画が現れます。



| |
| July 18, 2012 and May 14, 2013. | |
|
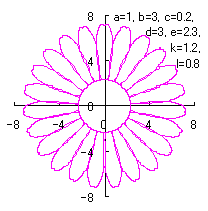
6.2.3 前節 6.2.2 の変形
|
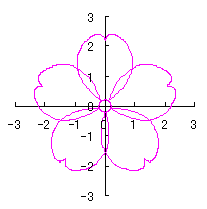 |
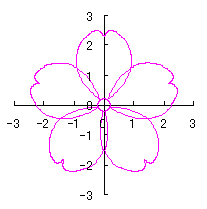 |
 |
|
d=1.25, e=0.2, k=0.75, l=1 |
d=1.3, e=0.2, k=0.75, l=1 |
d=3, e=2.3, k=1.2, l=0.8 |
|
上図を着色しますと次のようです。クリックすると拡大の線画が現れます。
  
| |
| July 22, 2012 and May 09, 2013. | |
|
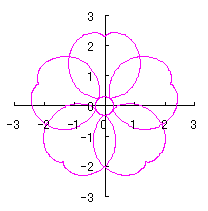
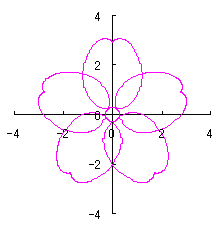
6.2.3 (ii) 前節 6.2.2 の変形(その2)
|
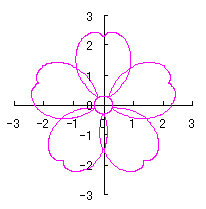 |
 |
 |
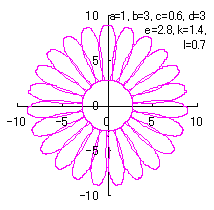 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
d=1.3, e=0.3, k=0.8, l=1 |
d=3, e=2.8, k=1.4, l=0.7 |
|
上図のうち図135c と図136 を着色しますと次のようです。クリックすると拡大の線画が現れます。
 
| |
| July 22, 2012 and May 09, 2013. | |
|
6.2.3 (iii) 前節 6.2.2 の変形(その3)
前節 6.2.2 の(72a)式と(72b)式にそれぞれ次の2式を置き換えます。
|
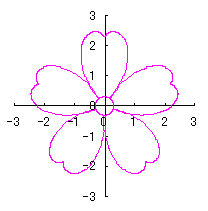 |
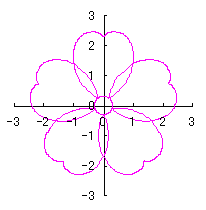 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
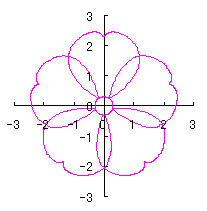
6.2.3 (iv) 前節 6.2.2 の変形(その4)
|
|
(クリックすると 拡大の線画が現れます) | |||
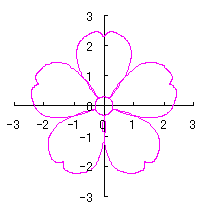 |
 |
 |
|
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
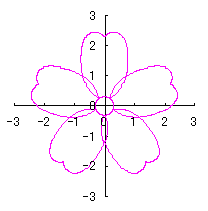
6.2.3 (v) 前節 6.2.2 の変形(その5)
|
 |
 |
 |
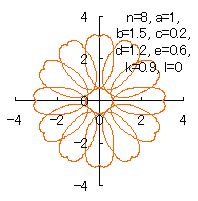 |
|
d=1, e=0.3, k=0.7, l=1 |
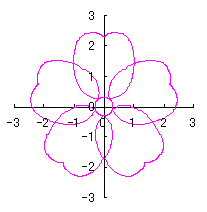
d=1, e=0.3, k=1, l=1 |
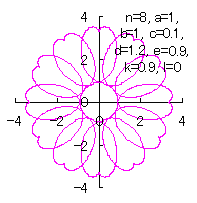
d=1.2, e=0.9, k=0.9, l=0 |
d=1.2, e=0.6, k=0.9, l=0 |
|
上図のうち図142a と図142b を着色しますと次のようです。クリックすると拡大の線画が現れます。 

6.2.3 (vi) 前節 6.2.2 の変形(その6)
|
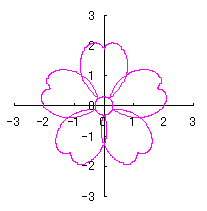 |
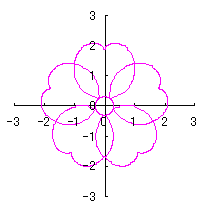 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
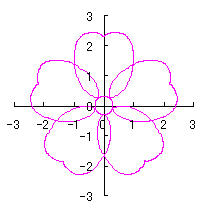
6.2.3 (vii) 前節 6.2.2 の変形(その7)
|
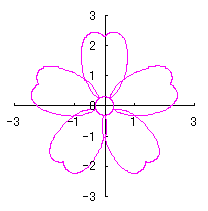 |
 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
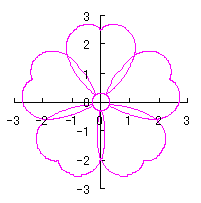
6.2.3 (viii) 前節 6.2.2 の変形(その8)
|
|
(クリックすると 拡大の線画が現れます) | ||||
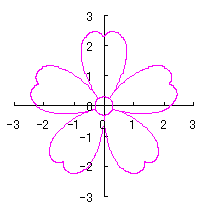 |
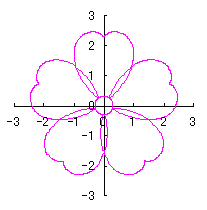 |
 |
 |
|
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
d=1.1, e=0.3, k=1.4, l=1 |
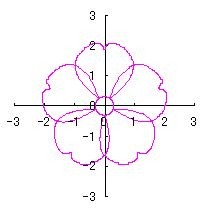
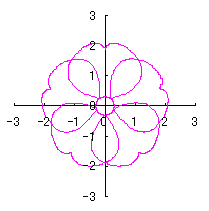
6.2.3 (iX) 前節 6.2.2 の変形(その9)
|
|
(クリックすると 拡大の線画が現れます) | ||||
 |
 |
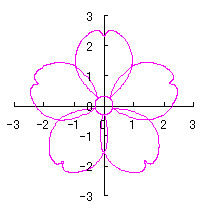 |
 |
|
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
d=1.25, e=0.3, k=0.7, l=1 |
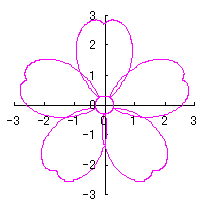
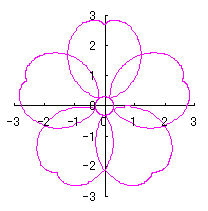
6.2.3 (x) 前節 6.2.2 の変形(その10)
|
 |
 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
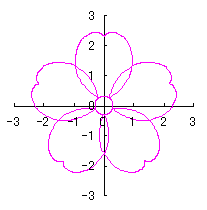
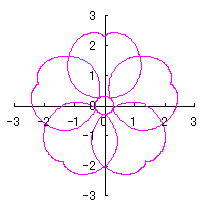
6.2.3 (xi) 前節 6.2.2 の変形(その11)
|
| (クリックすると拡大の線画が現れます) | |||
 |
 |
|
 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
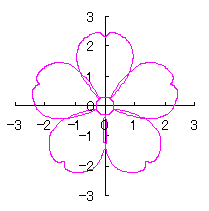
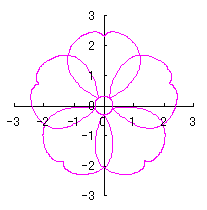
6.2.3 (xii) 前節 6.2.2 の変形(その12)
|
 |
 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
6.2.3 (xiii) 前節 6.2.2 の変形(その13) 前節 6.2.2 の(72a)式と(72b)式に次の式を置き換えます。 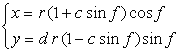 . (93) . (93)
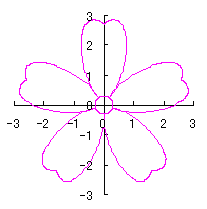
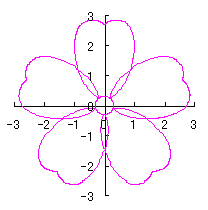
(71)式、(73)式から(80)式、および、(93)式を計算することにより、花の形の (x, y) 座標が求められます。こうして得られた図形の例を次に示します。ただし、 |
 |
 |
|
d=1, e=0.3, k=0.7, l=1 | d=1, e=0.3, k=1, l=1 |
6.2.3 (xiv) 前節 6.2.2 の変形(その14)
前節 6.2.2 の(72a)式と(72b)式に次の式を置き換えます。 |
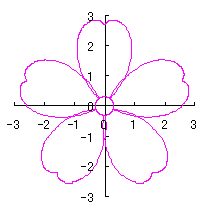 |
 |
|
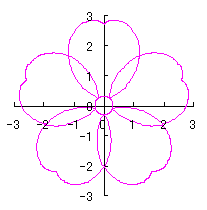
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
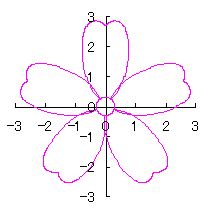
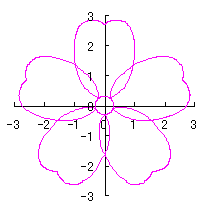
6.2.3 (xv) 前節 6.2.2 の変形(その15)
前節 6.2.2 の(72a)式と(72b)式に次の式を置き換えます。 |
 |
 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
| |
| July 25, 2012 | |
|
6.2.4 6.2.2 節の別変形について
|
| |||||||||||||||||||||||||||||||||||||||
|
|
July 29, 2012 and Apr. 04, 2013
|
|
| May 15, 2013 | |
|
6.2.4.b 別の関数として
別の関数として、
6.2.3 (ii) では「 y=d*r*(1-c*sin(f)*fabs(sin(f)))*sin(f)+2*a*d; 」を「 y=d*r*(1-c*sin(f)*fabs(sin(f)))*sin(f)+2*a*d*(1+c); 」に、
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| July 31, 2012 and Apr. 04, 2013 |
| ||||||||||||
|
||||||||||||
|
||||||||||||
|
|
| Aug. 01, 2012 and Apr. 02, 2013 |
| ||||||||||||||||||
|
|
Aug. 02, 2012
|
|||
| May 15, 2013 | |||
|
6.2.4.c 別の関数として考えられる他の関数
上記以外に、6.2.3 の各項に用いた |
|||
| July 31, 2012 | |||
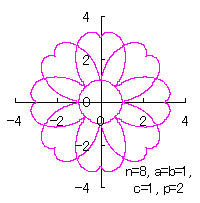
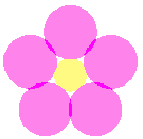
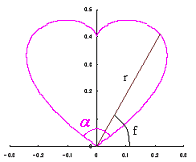
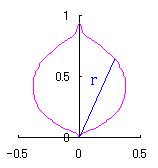
表題のような花びらは以下の方程式群から、
半径 |
|
(クリックすると 拡大の線画が現れます) | |||
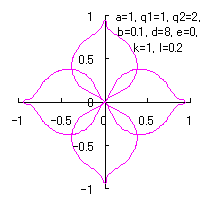 |
 |
|
|
|
d=8, e=0, k=1, l=0.2 |
|
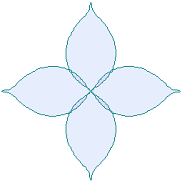
(クリックすると 拡大の線画が現れます) | ||
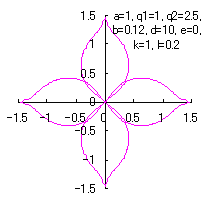 |
 |
|
|
d=8, e=0, k=1, l=0.2 |
|
| |
| June 17, 2013 | |
~ブラウザの「戻る」で 前に開いたページに戻ります~
~または、下のボタンを押して HOME に戻ります~
| HOME |
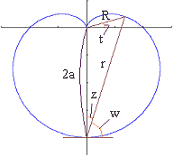
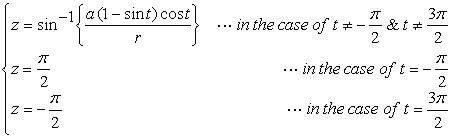 , (2)
, (2)
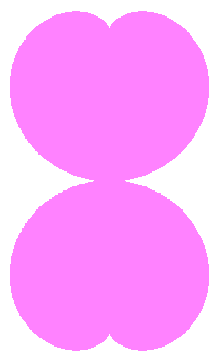















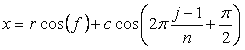 , (A2)
, (A2)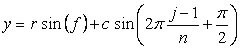 . (A3)
. (A3)
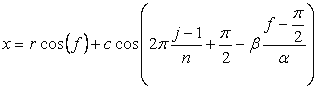 , (A4)
, (A4)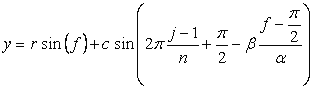 . (A5)
. (A5)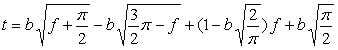 , (15)
, (15)
 . (21)
. (21)
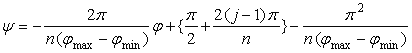 , (22)
, (22)

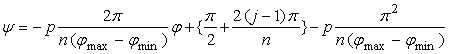 . (CI1)
. (CI1)
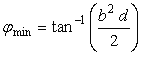 . (25)
. (25)
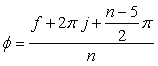 , (27)
, (27)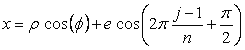 , (D1)
, (D1)
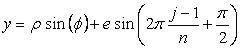 . (D2)
. (D2)
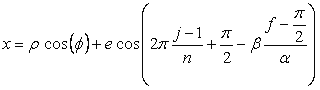 , (D3)
, (D3)
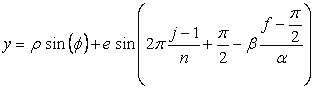 . (D4)
. (D4)
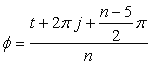 , (34)
, (34)
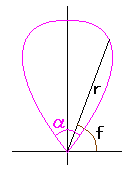
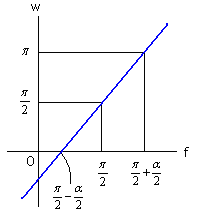
 . (44)
. (44)
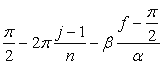 のように
のように 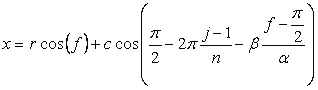 , (54)
, (54)
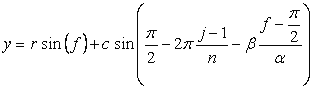 . (55)
. (55)
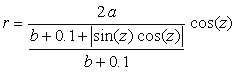 , (56-2)
, (56-2)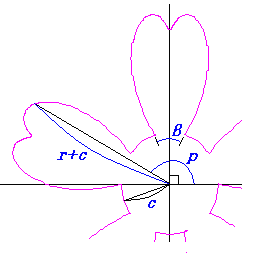
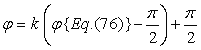 . (76b)
. (76b)
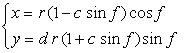 . (89)
. (89)
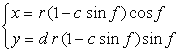 . (90)
. (90)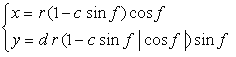 . (91)
. (91)
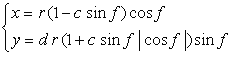 . (92)
. (92)
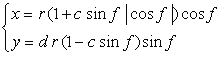 . (94)
. (94)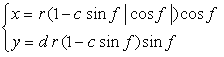 . (95)
. (95)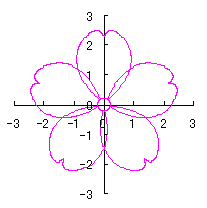
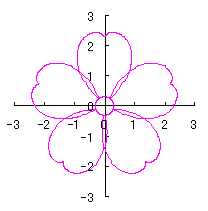


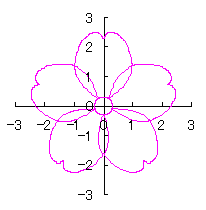

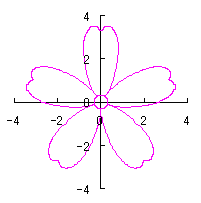
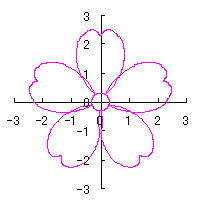
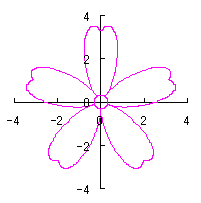
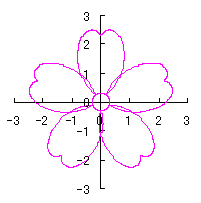
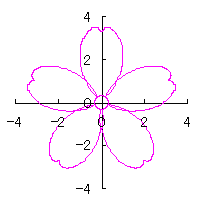
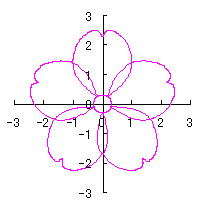

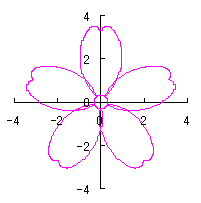





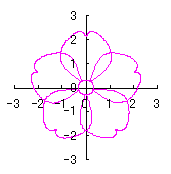
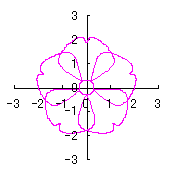
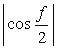 や
や 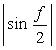 なども考えられます。
なども考えられます。
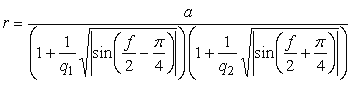 . (96a)
. (96a)
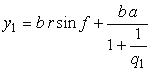 . (96c)
. (96c)
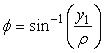 . (96e)
. (96e)
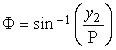 . (96i)
. (96i)
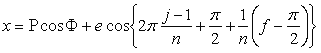 . (96j)
. (96j)
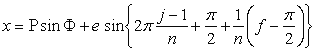 . (96k)
. (96k)