TDCC Laboratory
TDCC 研究室
| HOME | ENGLISH |
ハート形の曲線 II b
山本 信雄
本ページの図形は自由にコピーして自由にご使用できます。
|
1. はじめに
2. 基本式
|
 |
 |
|
|
|
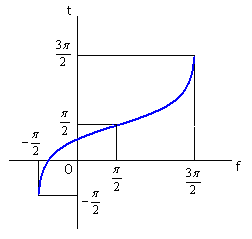 |
|
|
|
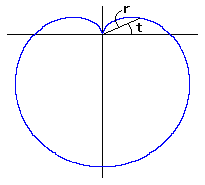
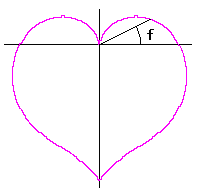
こうして、カージオイドの底に角度をなすように変換します。
3. 変換関数
|
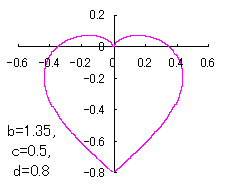 |
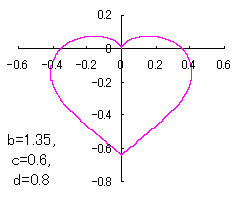 |
|
|
|
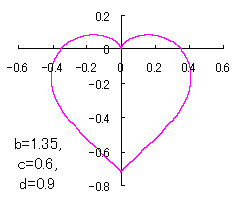 |
 |
|
|
|
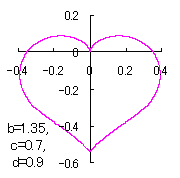 |
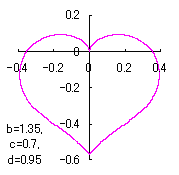 |
|
|
|
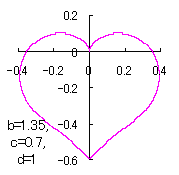 |
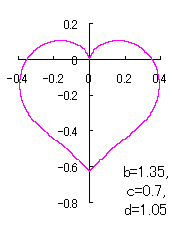 |
|
|
|
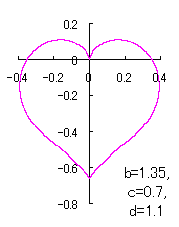 |
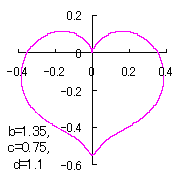 |
|
|
|
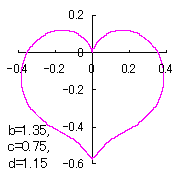 |
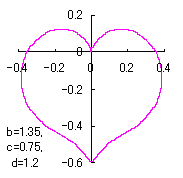 |
|
|
|
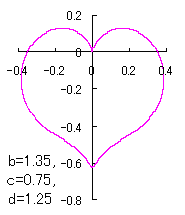 |
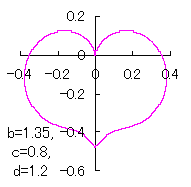 |
|
|
|
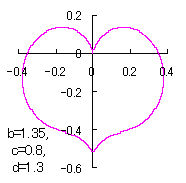 |
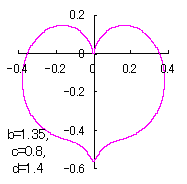 |
|
|
|
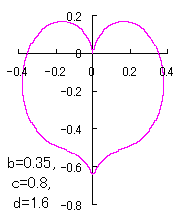 |
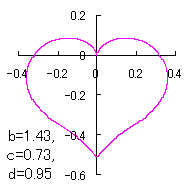 |
|
|
|
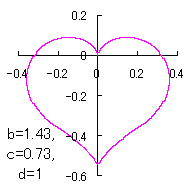 |
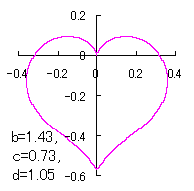 |
|
|
|
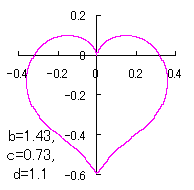 |
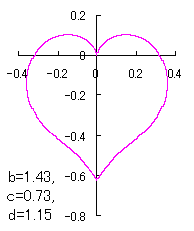 |
|
|
|
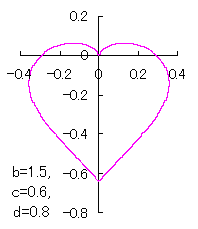 |
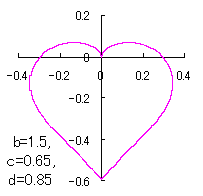 |
|
|
|
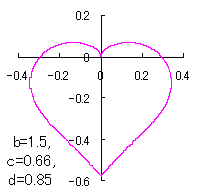 |
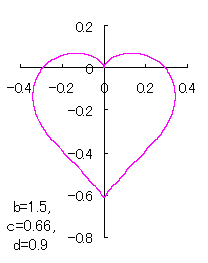 |
|
|
|
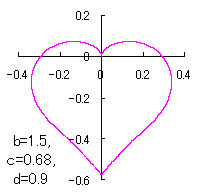 |
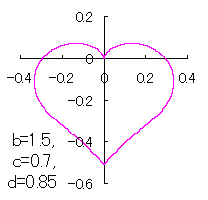 |
|
|
|
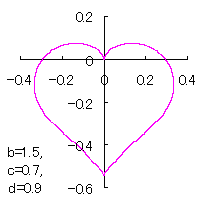 |
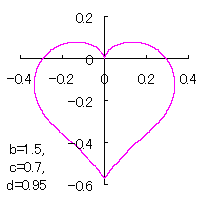 |
|
|
|
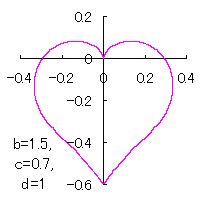 |
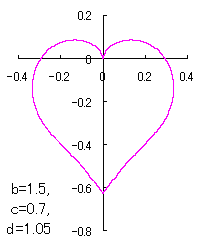 |
|
|
|
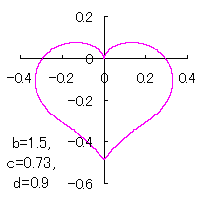 |
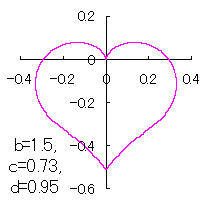 |
|
|
|
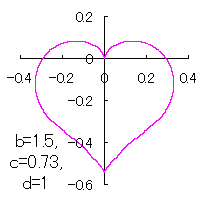 |
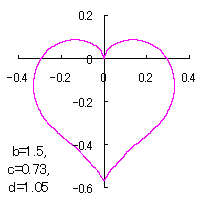 |
|
|
|
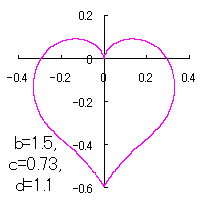 |
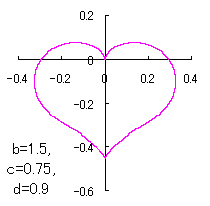 |
|
|
|
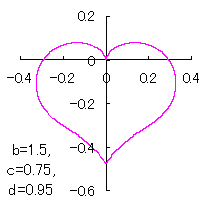 |
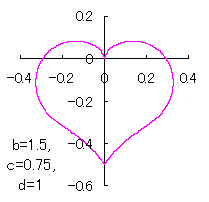 |
|
|
|
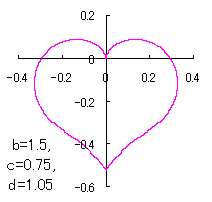 |
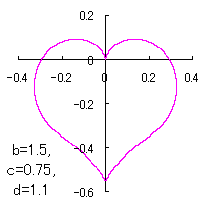 |
|
|
|
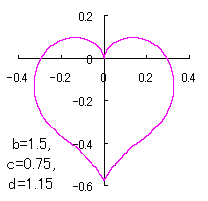 |
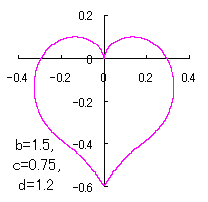 |
|
|
|
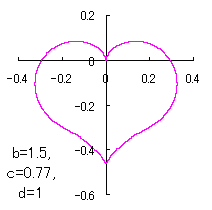 |
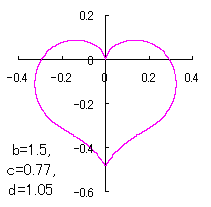 |
|
|
|
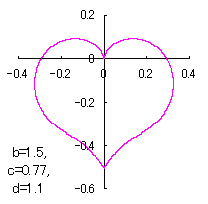 |
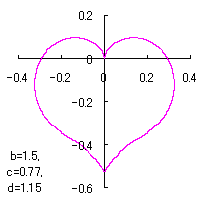 |
|
|
|
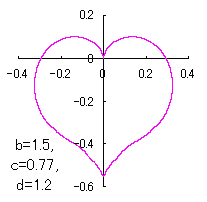 |
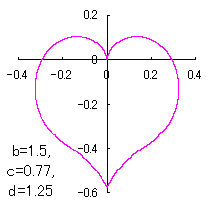 |
|
|
|
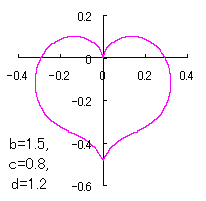 |
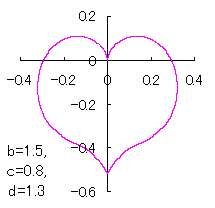 |
|
|
|
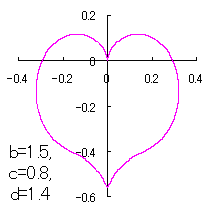 |
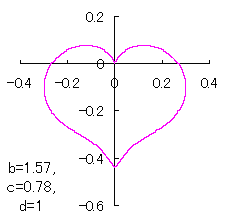 |
|
|
|
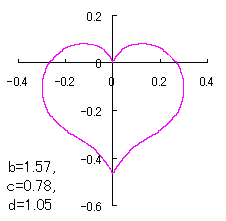 |
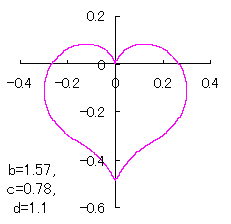 |
|
|
|
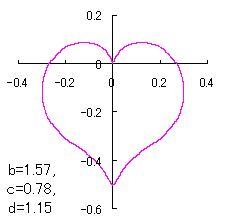 |
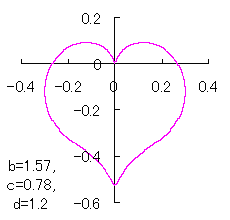 |
|
|
|
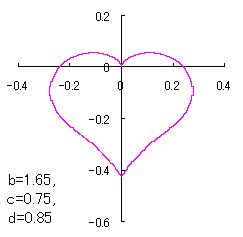 |
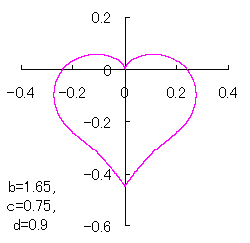 |
|
|
|
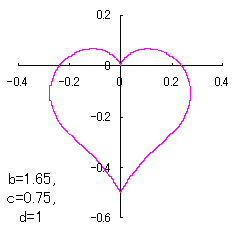 |
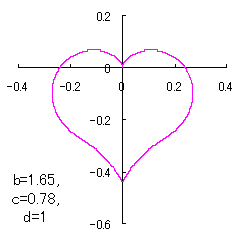 |
|
|
|
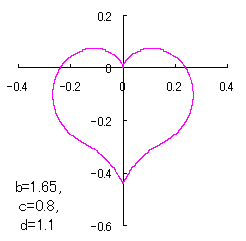 |
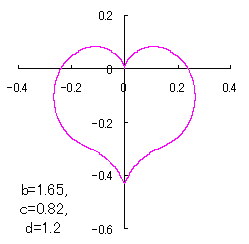 |
|
|
|
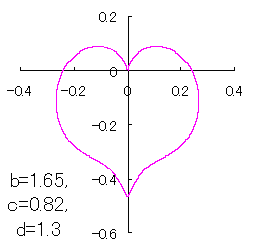 |
|
|
|
上図を着色すると次のようです。
これ以外にも別方法で得られるハート形がハート形曲線Ⅱ
(こちら
|
 |
|
|
|
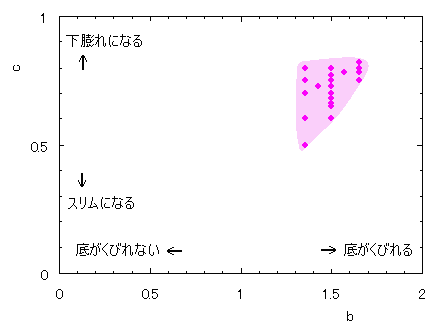
ピンク色が存在範囲で、複数のドット点がハート形曲線を 描かせたときのデータ点 |
 |
|
|
|
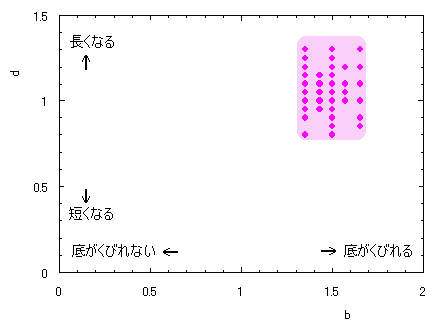
ピンク色が存在範囲で、複数のドット点がハート形曲線を 描かせたときのデータ点 |
 |
 |
|
|
|
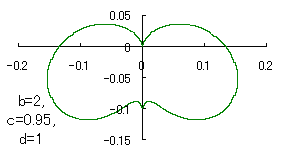 |
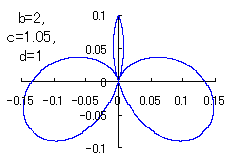 |
|
|
|
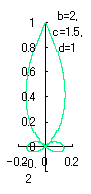 |
|
|
|
上図を着色すると次のようです。 4. 変換関数
|
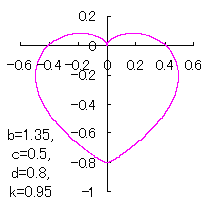 |
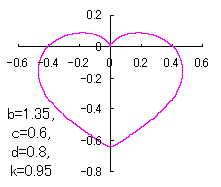 |
|
|
|
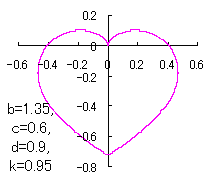 |
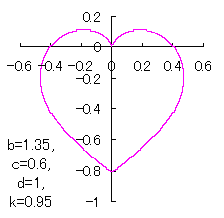 |
|
|
|
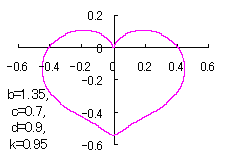 |
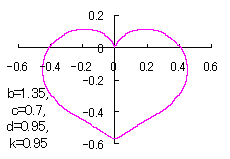 |
|
|
|
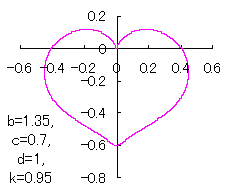 |
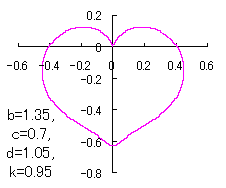 |
|
|
|
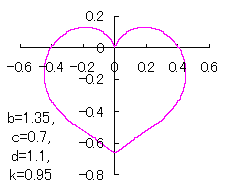 |
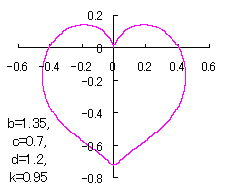 |
|
|
|
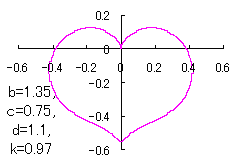 |
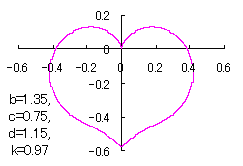 |
|
|
|
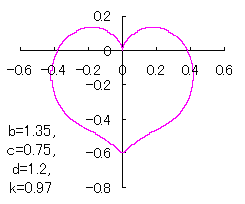 |
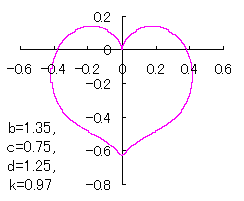 |
|
|
|
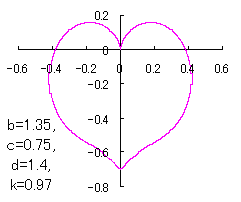 |
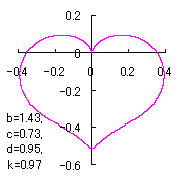 |
|
|
|
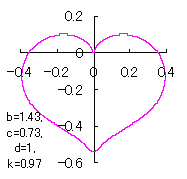 |
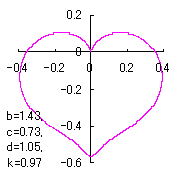 |
|
|
|
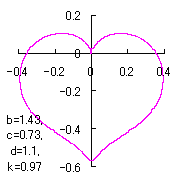 |
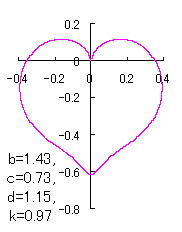 |
|
|
|
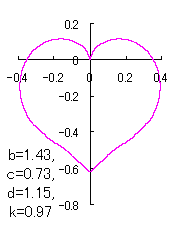 |
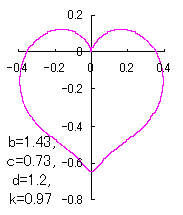 |
|
|
|
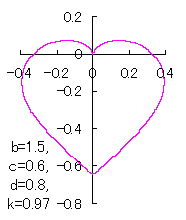 |
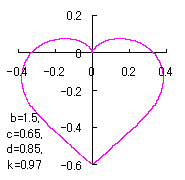 |
|
|
|
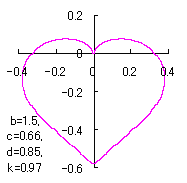 |
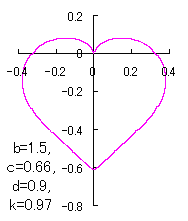 |
|
|
|
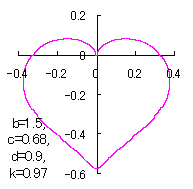 |
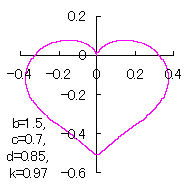 |
|
|
|
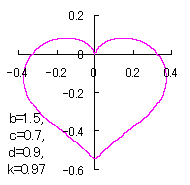 |
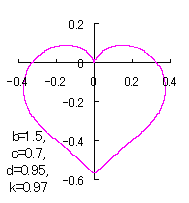 |
|
|
|
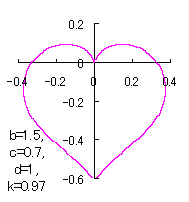 |
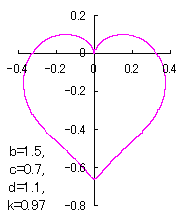 |
|
|
|
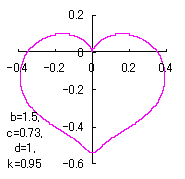 |
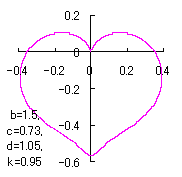 |
|
|
|
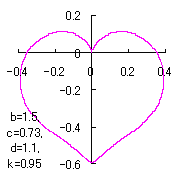 |
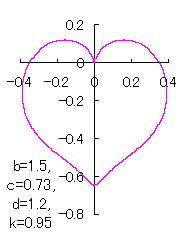 |
|
|
|
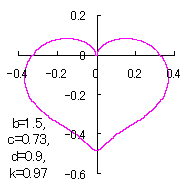 |
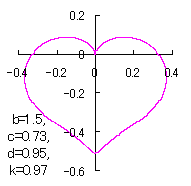 |
|
|
|
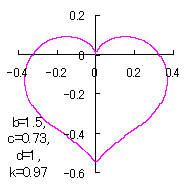 |
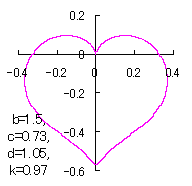 |
|
|
|
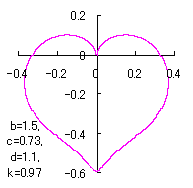 |
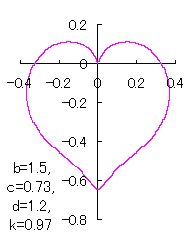 |
|
|
|
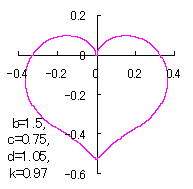 |
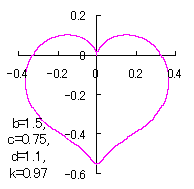 |
|
|
|
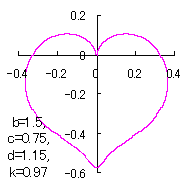 |
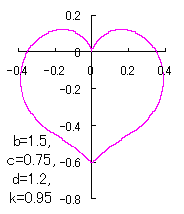 |
|
|
|
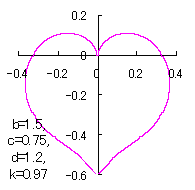 |
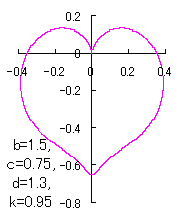 |
|
|
|
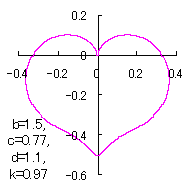 |
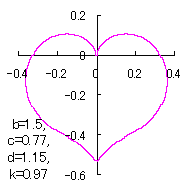 |
|
|
|
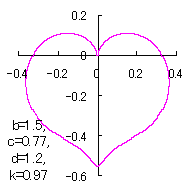 |
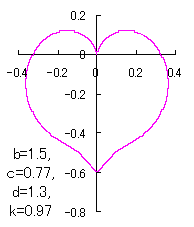 |
|
|
|
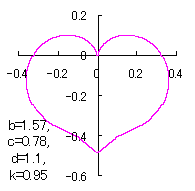 |
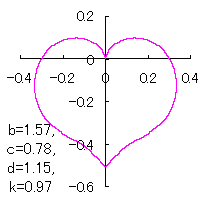 |
|
|
|
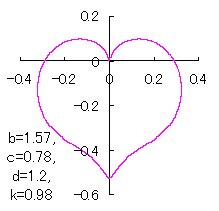 |
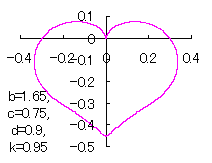 |
|
|
|
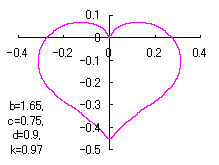 |
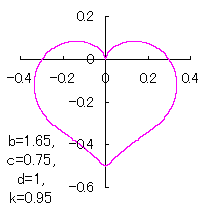 |
|
|
|
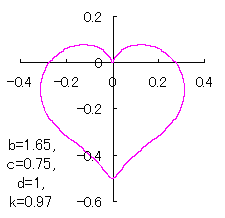 |
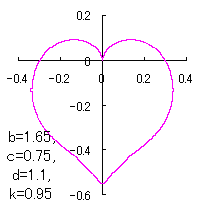 |
|
|
|
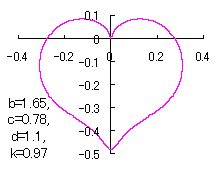 |
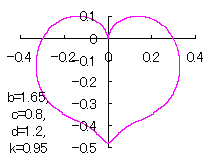 |
|
|
|
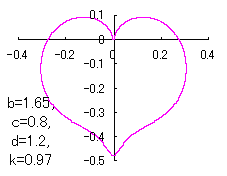 |
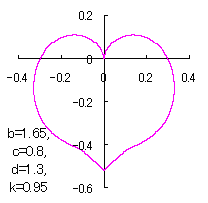 |
|
|
|
|
上図を着色すると次のようです。
これ以外にも別方法で得られるハート形がハート形曲線Ⅱ
(こちら
|
 |
|
|
|
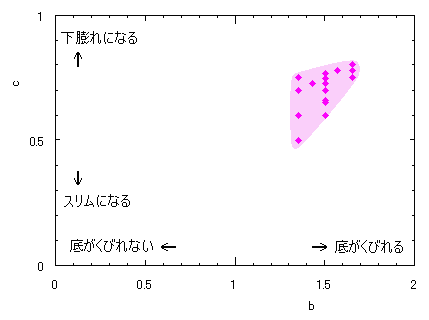
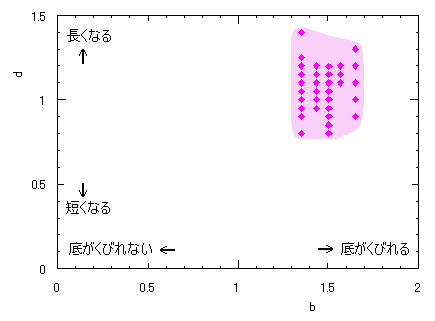
ピンク色が存在範囲で、複数のドット点がハート形曲線を描かせたとき のデータ点。なお、 |
 |
|
|
|
ピンク色が存在範囲で、複数のドット点がハート形曲線を描かせたとき のデータ点。なお、 |
5 変換関数
|
 |
 |
|
|
|
 |
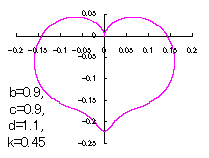 |
|
|
|
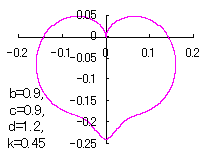 |
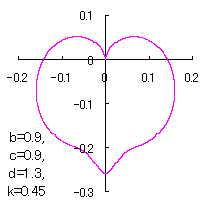 |
|
|
|
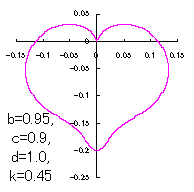 |
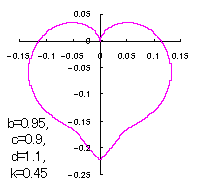 |
|
|
|
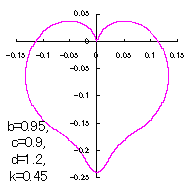 |
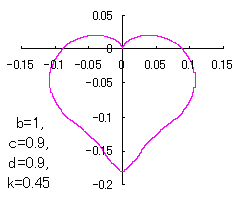 |
|
|
|
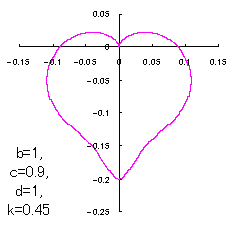 |
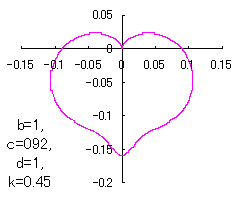 |
|
|
|
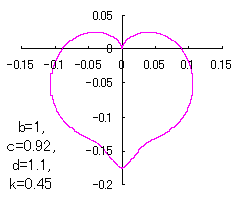 |
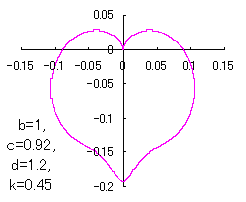 |
|
|
|
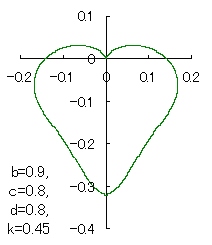 |
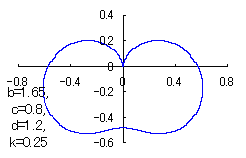 |
|
|
|
|
上図を着色すると次のようです。
6 変換関数
|
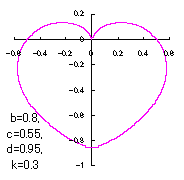 |
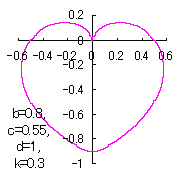 |
|
|
|
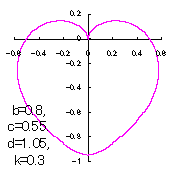 |
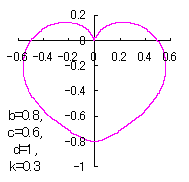 |
|
|
|
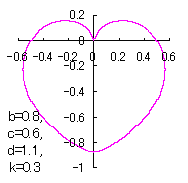 |
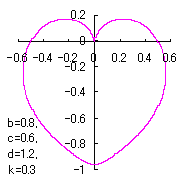 |
|
|
|
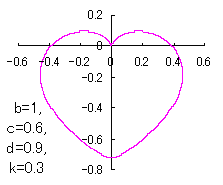 |
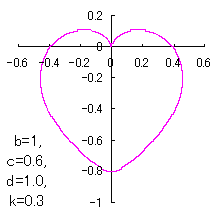 |
|
|
|
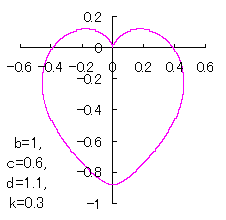 |
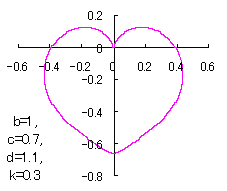 |
|
|
|
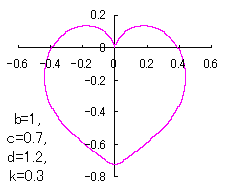 |
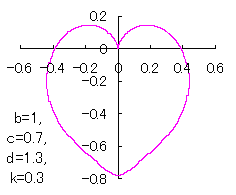 |
|
|
|
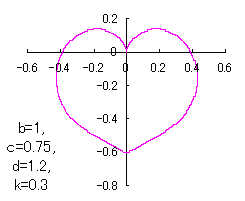 |
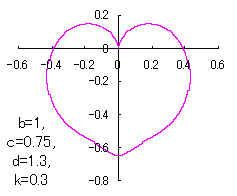 |
|
|
|
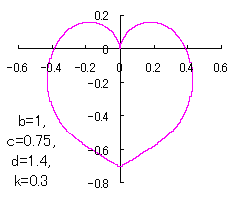 |
|
|
|
上図を着色すると次のようです。
7 変換関数
|
 |
 |
|
|
|
 |
 |
|
|
|
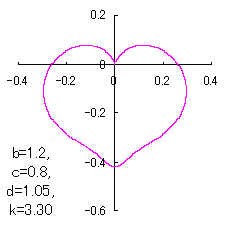 |
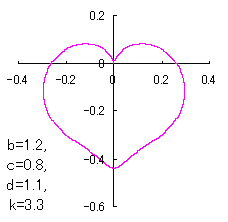 |
|
|
|
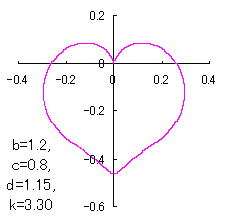 |
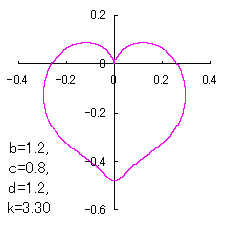 |
|
|
|
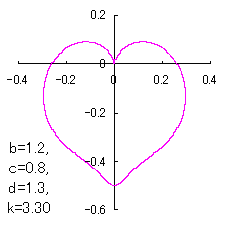 |
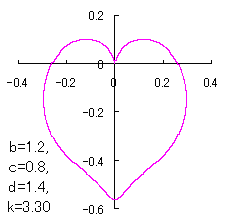 |
|
|
|
|
上図を着色すると次のようです。
|
~ブラウザの「戻る」で 前に開いたページに戻ります~
~または、下のボタンを押して HOME に戻ります~
| HOME |
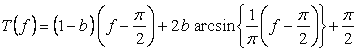 ,
(4)
,
(4)

































































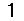




 ,
(5)
,
(5)
































































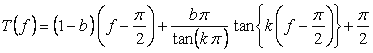 ,
(6)
,
(6)
















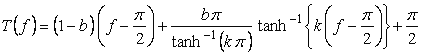 ,
(7)
,
(7)















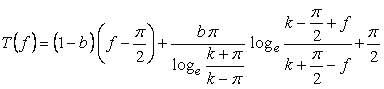 ,
(9)
,
(9)









