1. まえがき
Napierの自然数はEulerの数(下註)と並んで特異な値を持つことで知られる.線形系の解析解には Napier の自然数がその根幹を成している.
訳は、指数関数の微分が指数関数そのものである,という特性に基づいている.
本文では,その1つの根拠を,Napierの自然数の代数的な極限値としての表現と,指数関数の解析的取り扱いとの関連をもとに解き明かしてみようと思う.
(註) Eulerの数 は次式で得られる.[下記文献(1)]
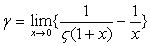 ,
ただし, ,
ただし,
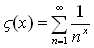 . .
2. 原方程式とその誘導
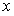 のすべての範囲で連続な2個の関数 のすべての範囲で連続な2個の関数 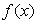 と と 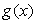 において、次の簡単な微分方程式 において、次の簡単な微分方程式
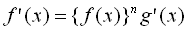 , (1) , (1)
の解は,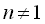 のときは のときは
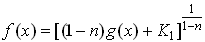 , (2) , (2)
であり, のときは のときは
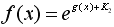 , (3) , (3)
であることは直ちに分かる.ただし,(1)式中の記号 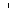 は微分を表す. は微分を表す.
 ,および, ,および,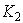 は積分定数であるが,(2)式と(3)式との関連性をもたせるとすると, は積分定数であるが,(2)式と(3)式との関連性をもたせるとすると,
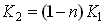 , (4) , (4)
でなければならない.
いま,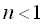 として,(2)式において として,(2)式において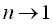 の極限をとると, の極限をとると,
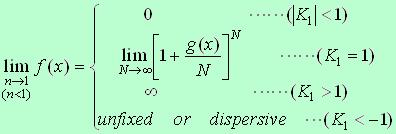 , (5) , (5)
ただし,
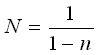 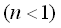 ,
(6) ,
(6)
と置いた.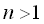 からのアプローチは,虚数を扱うことになるが,結果は同じである. からのアプローチは,虚数を扱うことになるが,結果は同じである.
(5)式により,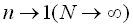 の極限での(2)式の解は, の極限での(2)式の解は,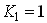 のときのみ成立することが分かる.このことが指数関数の由来と考えてよいであろう.
のときのみ成立することが分かる.このことが指数関数の由来と考えてよいであろう.
3. 指数関数の代数的極限値表現と解析関数表現
(5)式において,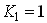 の場合を扱う.これは の場合を扱う.これは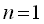 のときの(3)式と一致する筈なので,
次式を得る. のときの(3)式と一致する筈なので,
次式を得る.
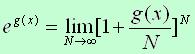 , (7) , (7)
なお,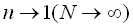 なので(4)式より, なので(4)式より,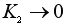 を考慮した. を考慮した.
(7)式の別表現は
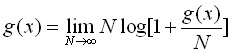 . (8) . (8)
(7)式右辺の冪級数展開を求めると,
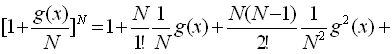 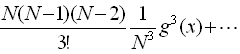 , (9) , (9)
となり,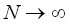 のときは のときは
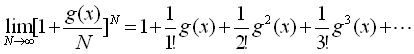 , (10) , (10)
となって,確かに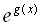 のテーラー展開となっている.このことから,(7)式の表現は,
その収束性がよくないと判断でき,(7),(9),(10)式の表現は現実の応用計算に向かないことが分かる.
しかし,指数関数の本質を理解する上で,本論は教育的効果があるかもしれない. のテーラー展開となっている.このことから,(7)式の表現は,
その収束性がよくないと判断でき,(7),(9),(10)式の表現は現実の応用計算に向かないことが分かる.
しかし,指数関数の本質を理解する上で,本論は教育的効果があるかもしれない.
4. おわりに
指数関数と代数的な極限値を結ぶ(7)式を得たが,求める過程の計算を目にする機会が殆どない.応用には向かないが,
本文での過程は指数関数の本質の1つの側面を見る面白さがあるのではないかと思う.
文 献
(1) 森口,宇田川,一松:数学公式Ⅰ,岩波全書,P.44,(1975).
[雑 談]
Napierの自然数は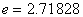 ,Eulerの数は ,Eulerの数は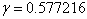 ,
円周率は ,
円周率は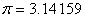 なので,次式が表記できます.
上記3定数の間には互いの関連が特にないと思われますが,この式の値は僅か 0.11 %の誤差で"1"になります. なので,次式が表記できます.
上記3定数の間には互いの関連が特にないと思われますが,この式の値は僅か 0.11 %の誤差で"1"になります.
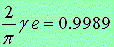 .
(11) .
(11)
これは偶然と思われますが,数学的にどうなっているのであろうか?
[参考] 誤差は 0.98 %とやや大きいですが,次の関係もあります.
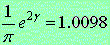 .
(12) .
(12)
[雑 談 2]
これも単なる数値合わせに過ぎませんが,次の近似も見つかりました.
僅か 0.037 %の誤差でNapierの自然数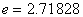 に近い. に近い.
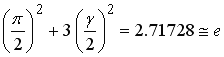 .
(13) .
(13)
[関連文献]
杉本氏の数学研究ノート
(その2)
に円周率をはじめとする諸定数の、数学的に厳密な級数展開や連分数展開、および、興味ある近似式が豊富に揃えられています。
|
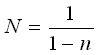
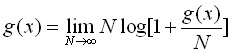 . (8)
. (8)
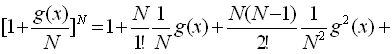
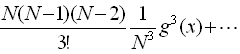 , (9)
, (9)
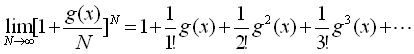 , (10)
, (10)
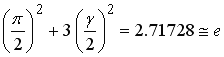 .
(13)
.
(13)