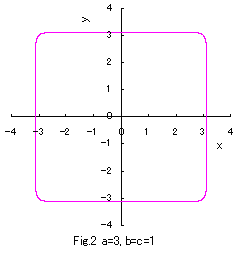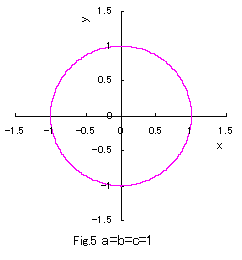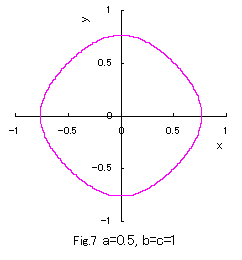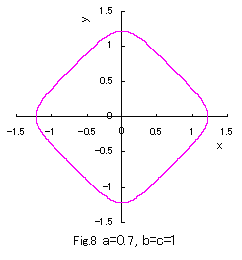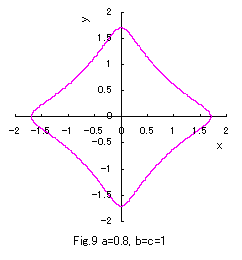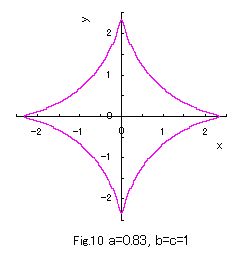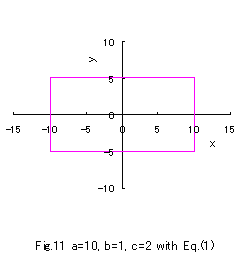|
There is a set of three equations described as below.
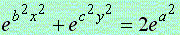 ,
(1) ,
(1)
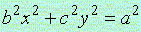 ,
(2) ,
(2)
and
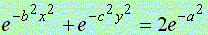 ,
(3) ,
(3)
where the values of a, b and c are arbitrary real numbers in Eqs.(1) and (2), and
where, in Eq.(3), the values of b and c are also arbitrary real numbers except for
the value of a which is restricted by the following equation.
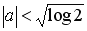 .
(4) .
(4)
In the case of 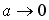 , it is shown in the foregoing calculations that
both of Eq.(1) and Eq.(3) are led to Eq.(2) by means of MacLaurin series expansion. , it is shown in the foregoing calculations that
both of Eq.(1) and Eq.(3) are led to Eq.(2) by means of MacLaurin series expansion.
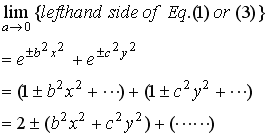 .
(5) .
(5)
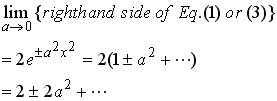 .
(6) .
(6)
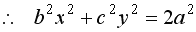 .
(7) .
(7)
As such the led Eq.(7) may be regarded to be an independent of Eqs.(1) and (3), we can remove the coefficient number "2"
from the right-hand side 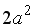 of Eq.(7) freely.
Thus, the constants a, b and c in Eq.(2) are newly defined as arbitrary real numbers. of Eq.(7) freely.
Thus, the constants a, b and c in Eq.(2) are newly defined as arbitrary real numbers.
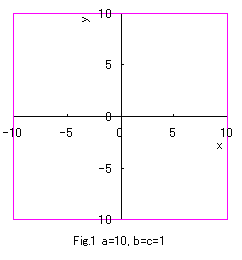
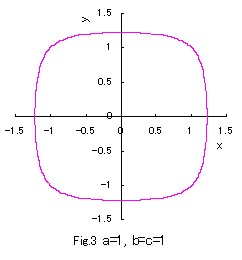
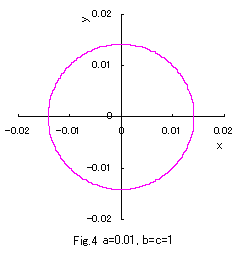
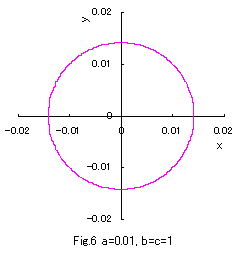
In the case of b=c=1, if Eqs.(1) to (3) are numerically calculated
and graphically displayed in the various values of a with the use of a computer,
the various closed-curves related to a are obtained as shown in Figs.1 to 10.
Eq.(1), Eq.(2) and Eq.(3) give convex, true and concave circles respectively.
Moreover, Eq,(1) nearly gives rectangles under sufficiently large values of a, and Eq.(3) nearly gives an asteroid
under the minimum value of a which is restricted in the defined region as given in Eq.(4).
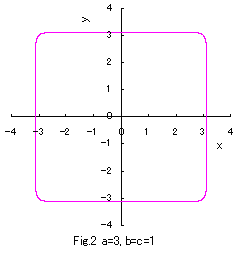
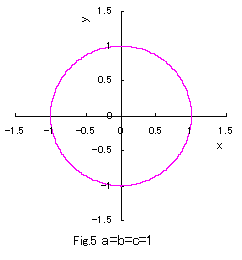
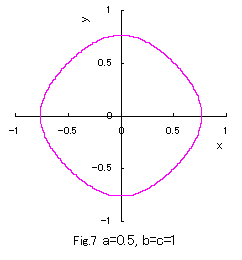
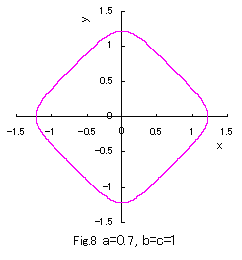
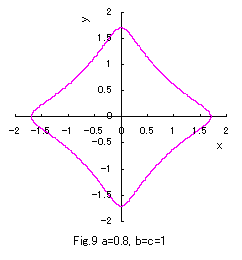
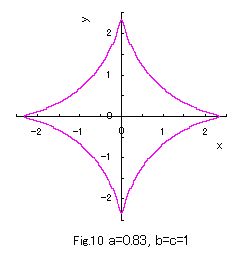
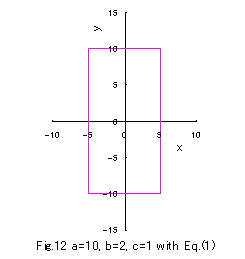
When a takes sufficiently large value, Eq,(1) gives rectangles which have different sizes between longitudinal
and horizontal sides as varying the values of b and c in the same manner as in another way
in this button
 .
When a=10, two cases of b=1 and c=2, and b=2 and c=1 are displayed in the followings. .
When a=10, two cases of b=1 and c=2, and b=2 and c=1 are displayed in the followings.
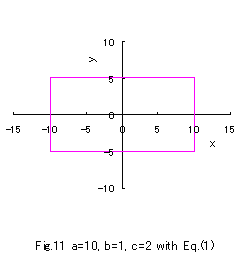
[Reference]
General Method
Generally, the convex, true and concave circles or ellipses are given by the following equation.
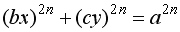 ,
(8) ,
(8)
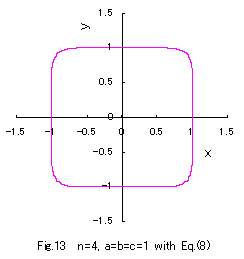
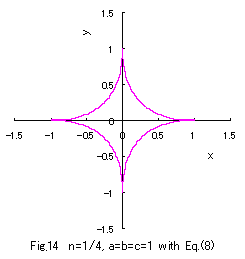
Two examples of the cases of b=1 and c=2, and b=2 and c=1 are shown in Fig.13 and Fig.14 respectively.
|
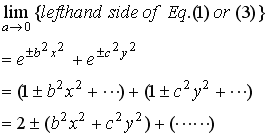 .
(5)
.
(5)
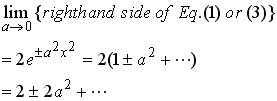 .
(6)
.
(6)