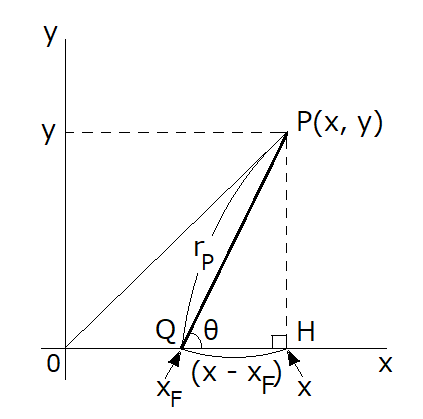
図1 卵形曲線を描くP点の説明
|
「卵形曲線を表す方程式」の本文にも記述しましたように、発想の基礎になる図が右図です。
図中、点 P、並びに、点 Q の座標はそれぞれ P(x, y)、および、Q(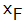 , 0) です。
図中の各変数は、本文で述べたように、次の 2 式のような仮定があります。 , 0) です。
図中の各変数は、本文で述べたように、次の 2 式のような仮定があります。
|
|
\begin{align}
x_{ F }=ℓ\cos \theta
\end{align}
|
(A1)
|
|
|
\begin{align}
r_{ F }=a_{ P }+b_{ P }\cos \theta
\end{align}
|
(A2)
|
右図の直角三角形 PQH に於いて、次の2式が成り立ちます。
|
|
\begin{align}
x-x_{ F }=r_{ P }\cos \theta
\end{align}
|
(A3)
|
|
|
\begin{align}
y=r_{ P }\sin \theta
\end{align}
|
(A4)
|
また、直角三角形 PQH に於けるピタゴラスの定理により、
|
|
\begin{align}
r_{ P }^{ 2 }=(x-x_{ F })^{ 2 }+y^{ 2 }
\end{align}
|
(A5)
|
これに (2) 式と (1) 式を代入すると、
|
|
\begin{align}
(a_{ P }+b_{ P }\cos \theta)^{ 2 }=(x-ℓ\cos \theta)^{ 2 }+y^{ 2 }
\end{align}
|
(A6)
|
|
|
\begin{align}
∴a_{ P }^{ 2 }+2a_{ P }b_{ P }\cos \theta+b_{ P }^{ 2 }\cos^{ 2 } \theta=x^{ 2 }-2ℓx\cos \theta+ℓ^{ 2 }\cos^{ 2 } \theta+y^{ 2 }
\end{align}
|
これを整理して
|
|
\begin{align}
x^{ 2 }+y^{ 2 }-2(ℓx+a_{ P }b_{ P })\cos \theta-[a_{ P }^{ 2 }+(b_{ P }^{ 2 }-ℓ^{ 2 })\cos^{ 2 } \theta]=0
\end{align}
|
(A7)
|
本文にも書きましたように、取り扱いを容易にするために (解析的に解けるように)
|
|
\begin{align}
b_{ P }=ℓ
\end{align}
|
(A8)
|
と仮定します。上式を (A7) 式に代入して
|
|
\begin{align}
x^{ 2 }+y^{ 2 }-a_{ P }^{ 2 }-2(ℓx+a_{ P }ℓ)\cos \theta=0
\end{align}
|
(A9)
|
|
|
\begin{align}
∴\cos \theta= \frac{x^{ 2 }+y^{ 2 }-a_{ P }^{ 2 }}{2ℓ(x+a_{ P })}
\end{align}
|
(A10)
|
また、(A9) 式を次のように変形します。
|
|
\begin{align}
x^{ 2 }+y^{ 2 }-2(x+a_{ P })(a_{ P }+ℓ\cos \theta)+2(x+a_{ P })a_{ P }-a_{ P }^{ 2 }=0
\end{align}
|
|
|
\begin{align}
∴x^{ 2 }+y^{ 2 }-2(x+a_{ P })(a_{ P }+ℓ\cos \theta)+2a_{ P }x+a_{ P }^{ 2 }=0
\end{align}
|
(A11)
|
ところで、(A8) 式を (A2) 式に代入して、
|
|
\begin{align}
r_{ P }=a_{ P }+ℓ\cos \theta
\end{align}
|
(A12)
|
これを (A4) 式に代入すると
|
|
\begin{align}
y=(a_{ P }+ℓ\cos \theta)\sin \theta
\end{align}
|
(A13)
|
一方、(A11) 式に sin θ をかけると
|
|
\begin{align}
(x^{ 2 }+y^{ 2 }+2a_{ P }x+a_{ P }^{ 2 })\sin \theta-2(x+a_{ P })(a_{ P }+ℓ\cos \theta)\sin \theta=0
\end{align}
|
(A14)
|
(A14) 式左辺の最後の項に (A13) 式を代入して。
|
|
\begin{align}
(x^{ 2 }+y^{ 2 }+2a_{ P }x+a_{ P }^{ 2 })\sin \theta-2(x+a_{ P })y=0
\end{align}
|
|
|
\begin{align}
∴\sin \theta = \frac{2(x+a_{ P })y}{(x+a_{ P })^{ 2 }+y^{ 2 }}
\end{align}
|
(A15)
|
三角公式は
|
|
\begin{align}
\sin^{ 2 } \theta+\cos^{ 2 } \theta=1
\end{align}
|
(A16)
|
(A10) 式と (A15) 式を上式に代入して
|
|
|
\begin{align}
\frac{(x^{ 2 }+y^{ 2 }-a_{ P }^{ 2 })^{ 2 }}{4ℓ^{ 2 }(x+a_{ P })^{ 2 }} + \frac{4(x+a_{ P })^{ 2 }y^{ 2 }}{[(x+a_{ P })^{ 2 }+y^{ 2 }]^{ 2 }}=1
\end{align}
|
|
(A17)
|
が得られます。これがホームページ本文の (7) 式です。
|