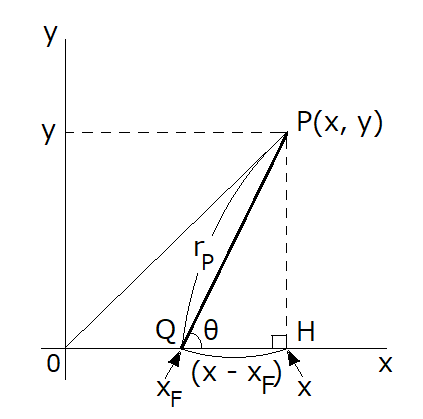
Fig.1 Explanation of the Point P which draws egg-shaped curve
|
As described in the text of "Equation of Egg Shaped Curve of the Actual Egg is Found", the basis of the idea is shown in Fig.1.
In this figure, the coordinates of points P and Q are P (x, y) and Q (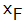 , 0), respectively.
As mentioned in the text, each variable in Fig.1 has the following two assumptions.
|
|
\begin{align}
x_{ F }=ℓ\cos \theta
\end{align}
|
(A1)
|
|
|
\begin{align}
r_{ F }=a_{ P }+b_{ P }\cos \theta
\end{align}
|
(A2)
|
In regard to the triangle PQH in Fig.1, the following two equations are given.
|
|
\begin{align}
x-x_{ F }=r_{ P }\cos \theta
\end{align}
|
(A3)
|
|
|
\begin{align}
y=r_{ P }\sin \theta
\end{align}
|
(A4)
|
Also, according to the Pythagorean theorem in the triangle PQH in Fig.1,
|
|
\begin{align}
r_{ P }^{ 2 }=(x-x_{ F })^{ 2 }+y^{ 2 }
\end{align}
|
(A5)
|
Substituting Eqs. (2) and (1) into the above equation,
|
|
\begin{align}
(a_{ P }+b_{ P }\cos \theta)^{ 2 }=(x-ℓ\cos \theta)^{ 2 }+y^{ 2 }
\end{align}
|
(A6)
|
|
|
\begin{align}
∴a_{ P }^{ 2 }+2a_{ P }b_{ P }\cos \theta+b_{ P }^{ 2 }\cos^{ 2 } \theta=x^{ 2 }-2ℓx\cos \theta+ℓ^{ 2 }\cos^{ 2 } \theta+y^{ 2 }
\end{align}
|
After rearranging the above equation, we may write the follows.
|
|
\begin{align}
x^{ 2 }+y^{ 2 }-2(ℓx+a_{ P }b_{ P })\cos \theta-[a_{ P }^{ 2 }+(b_{ P }^{ 2 }-ℓ^{ 2 })\cos^{ 2 } \theta]=0
\end{align}
|
(A7)
|
As written in the text, for to be solved analytically, we assume the following relation.
|
|
\begin{align}
b_{ P }=ℓ
\end{align}
|
(A8)
|
Substituting the above equation into Eq.(A7),
|
|
\begin{align}
x^{ 2 }+y^{ 2 }-a_{ P }^{ 2 }-2(ℓx+a_{ P }ℓ)\cos \theta=0
\end{align}
|
(A9)
|
|
|
\begin{align}
∴\cos \theta= \frac{x^{ 2 }+y^{ 2 }-a_{ P }^{ 2 }}{2ℓ(x+a_{ P })}
\end{align}
|
(A10)
|
Also, rewriting equation (A9) as follows.
|
|
\begin{align}
x^{ 2 }+y^{ 2 }-2(x+a_{ P })(a_{ P }+ℓ\cos \theta)+2(x+a_{ P })a_{ P }-a_{ P }^{ 2 }=0
\end{align}
|
|
|
\begin{align}
∴x^{ 2 }+y^{ 2 }-2(x+a_{ P })(a_{ P }+ℓ\cos \theta)+2a_{ P }x+a_{ P }^{ 2 }=0
\end{align}
|
(A11)
|
By the way, by substituting Eq.(A8) into Eq.(A2),
|
|
\begin{align}
r_{ P }=a_{ P }+ℓ\cos \theta
\end{align}
|
(A12)
|
Substituting the above equation into Eq.(A4),
|
|
\begin{align}
y=(a_{ P }+ℓ\cos \theta)\sin \theta
\end{align}
|
(A13)
|
On the other hand, when sin θ is multiplied by Eq. (A11),
|
|
\begin{align}
(x^{ 2 }+y^{ 2 }+2a_{ P }x+a_{ P }^{ 2 })\sin \theta-2(x+a_{ P })(a_{ P }+ℓ\cos \theta)\sin \theta=0
\end{align}
|
(A14)
|
Substituting Eq.(A13) in the last term of the left hand side of Eq.(A14), Eq.(A14) leads to
|
|
\begin{align}
(x^{ 2 }+y^{ 2 }+2a_{ P }x+a_{ P }^{ 2 })\sin \theta-2(x+a_{ P })y=0
\end{align}
|
|
|
\begin{align}
∴\sin \theta = \frac{2(x+a_{ P })y}{(x+a_{ P })^{ 2 }+y^{ 2 }}
\end{align}
|
(A15)
|
The trigonometric formula is
|
|
\begin{align}
\sin^{ 2 } \theta+\cos^{ 2 } \theta=1
\end{align}
|
(A16)
|
Substituting Eqs.(A10) and (A15) into the above equation, the following equation is derived.
|
|
|
\begin{align}
\frac{(x^{ 2 }+y^{ 2 }-a_{ P }^{ 2 })^{ 2 }}{4ℓ^{ 2 }(x+a_{ P })^{ 2 }} + \frac{4(x+a_{ P })^{ 2 }y^{ 2 }}{[(x+a_{ P })^{ 2 }+y^{ 2 }]^{ 2 }}=1
\end{align}
|
|
(A17)
|
This is exactly the Eq.(7) in the text of the homepage.
|
