TDCC Laboratory
| HOME | JAPANESE |
Equation of Egg Shaped Curve IV (Egg Shaped Curve II proposed by Mr. Asai)
Mr. Yasuyuki ASAI (Machida city, Tokyo, Japan) and Nobuo YAMAMOTO
Mr. Yasuyuki ASAI has informed more novel types of egg shaped curves to Yamamoto in September, 2009.
This thesis is described by YAMAMOTO in account of these novel two types of the equations expressing the egg shaped curves.
|
This site is introduced in
GENERATING AVIAN EGG USING RATIONAL BEZIER QUADRATIC CURVES and
Make An Egg-Shaped Model With Origami.
|
1. The first type of equation (extend the ellipse non-uniformly along the y-axis)
One of two novel types of the equations expressing egg shaped curve proposed by Mr. Yasuyuki ASAI is written in the following;
Eq.(1) is transformed into the following equation. 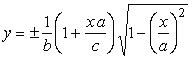 . (2) . (2)
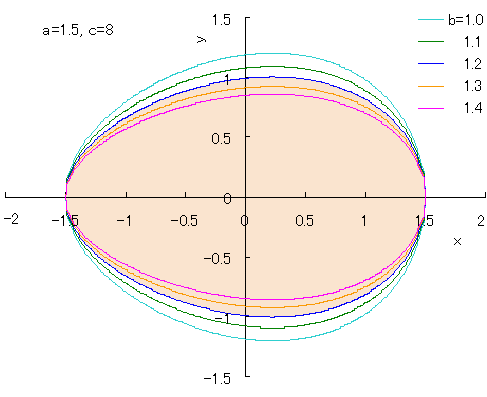
If we calculate Eq.(2) as varying several values of b with the use of computer, we obtain Fig.1. Thus, we may find egg shaped curves as seen in Fig.1. Comparison between the curve in the case that a=1.5, b=1.05 and c=11 and the shape of an actual egg is shown in Fig.2. As seen in Fig.2, the egg shaped curve may approximately coincide to the shape of an actual egg. |
2. The second type of equation
Another one of two novel types of the equations expressing egg shaped curve proposed by Mr. Yasuyuki ASAI is written in the following;
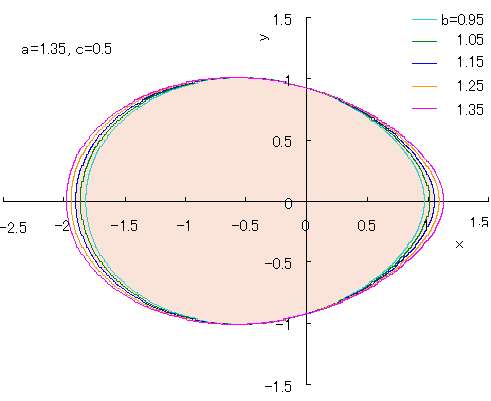
If we calculate Eq.(3) as varying the several values of b with the use of computer, we obtain Fig.3. Thus, we may find egg shaped curves as seen in Fig.3. Comparison between the curve in the case that a=1.35, b=0.9 and c=0.5 and the shape of an actual egg is shown in Fig.4. As seen in Fig.4, the egg shaped curve may approximately coincide to the shape of an actual egg. 3. A conventional method to connect two ellipsoids into an egg shaped curve
A simple method to connect two ellipsoids into an egg shaped curve is also proposed by Mr. Yasuyuki ASAI. The equation for expressing such an egg shaped curve is written in the following;
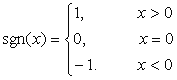 . (5) . (5)
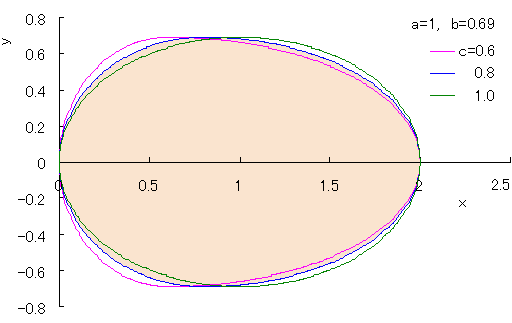
In the case of c=a, Eq.(4) gives an ellipsoid. If we calculate Eq.(4) as varying the several values of c with the use of computer, we obtain Fig.5. Comparison between the curve in the case that a=1, b=0.72 and c=0.9 and the shape of an actual egg is shown in Fig.6. As seen in Fig.6, the egg shaped curve may approximately coincide to the shape of an actual egg. |
_ returning to the page which opened just before with 'return' of browser _
or
_ returning to the HOME with the following button _
| HOME |