1. Expression by the 2nd order exponential function
We treat the equation given below.
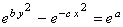 ,
(1a) ,
(1a)
where b > 0 and c > 0. The solution of the above equation is obtained as
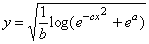 ,
(2a) ,
(2a)
where the following condition must be needed only in the case of a < 0.
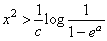 .
(3a) .
(3a)
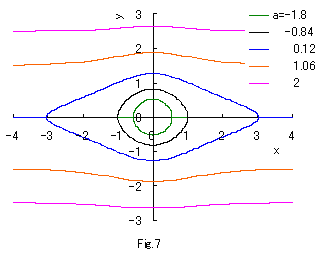
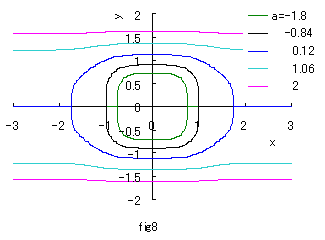
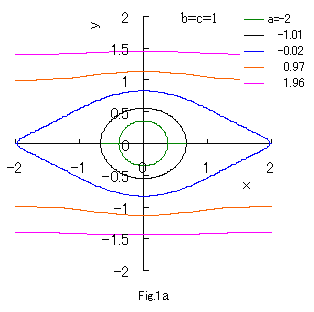
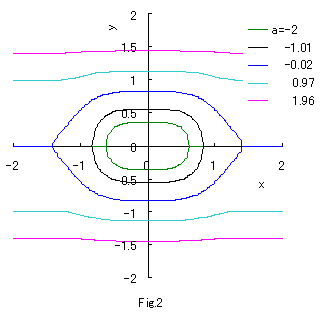
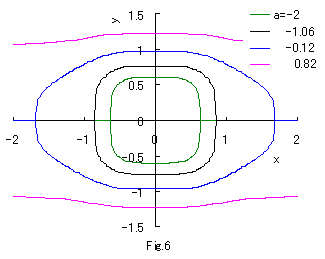
If we calculate Eq.(2a) numerically with the use of computer in the case of b=c=1, eye shaped curves are drawn as shown in Fig.1a.
|
A C++ program, with which the numerical calculation of Eq.(2a) is executed to obtain the curves shown in Fig.1a,
is given by
 . .
|
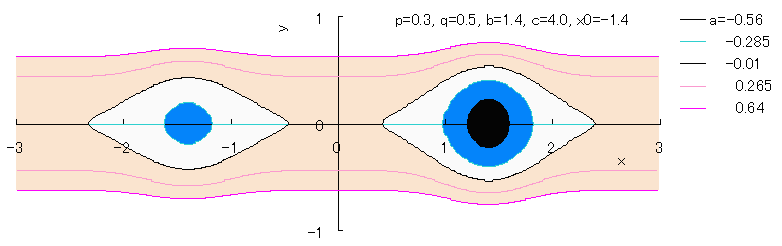
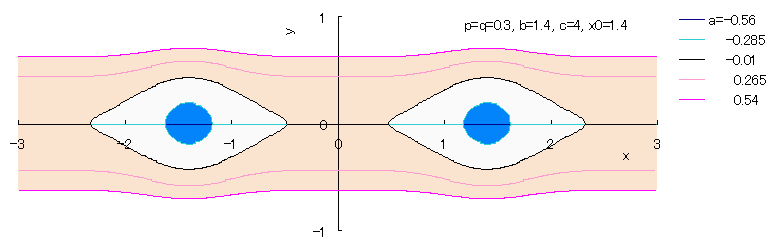
In the next, the equation which expresses the both eyes with the use of two figures of Fig.1a is described as
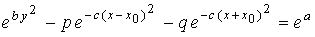 ,
(1b) ,
(1b)
where b > 0 and c > 0. The solution of the above equation is obtained as
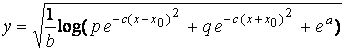 ,
(2b) ,
(2b)
where the following condition must be needed only in the case of a < 0.
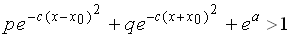 .
(3b) .
(3b)
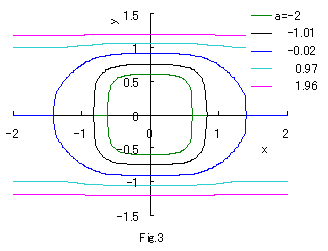
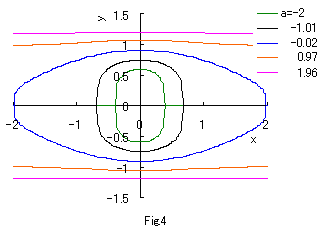
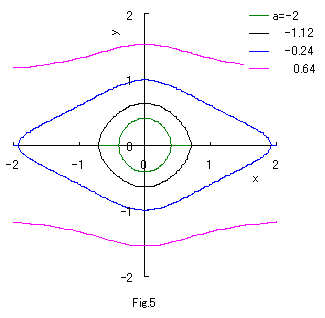
If we calculate Eq.(2b) numerically with the use of computer, curves of both eyes are drawn as shown
in the following figures.
|
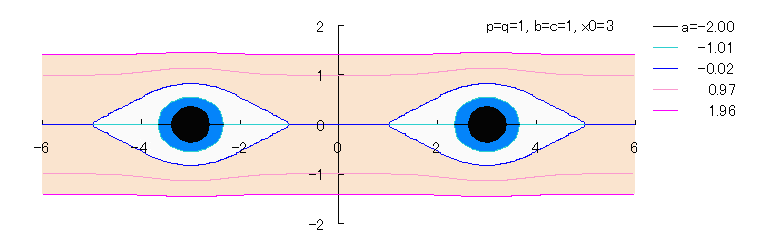
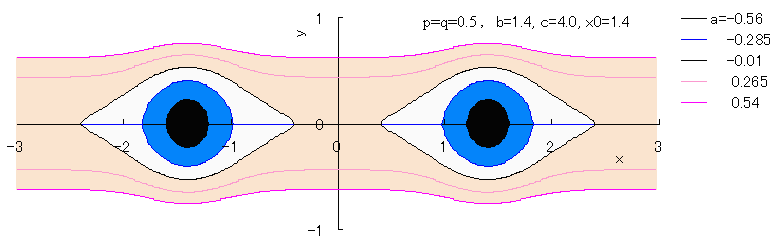
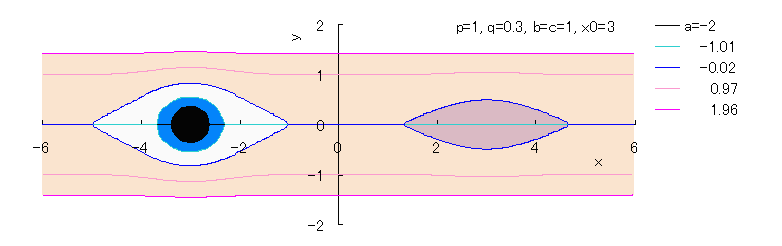

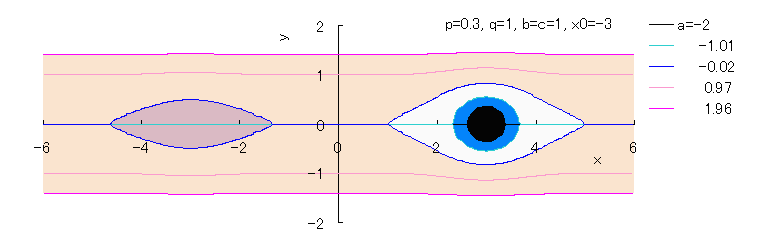



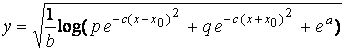 ,
(2b)
,
(2b)
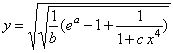 ,
(15)
,
(15)