TDCC Laboratory
| HOME | JAPANESE |
Flower Graphics
Nobuo YAMAMOTO
You can copy and use all the figures in this page freely.
|
|

|
|
1. Preface
We try to produce shape of flower by calculation with the use of computer as an application of "heart curves II" treated in the other page of this home page. According to two kinds of methods written in the page of "heart curves II", these two methods will be followed also in this page. 2. Method 1
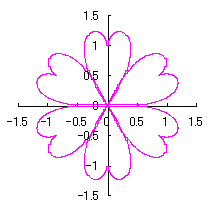
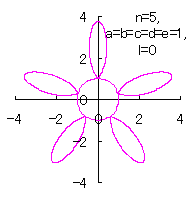
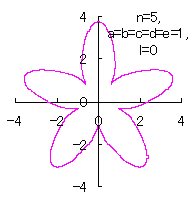
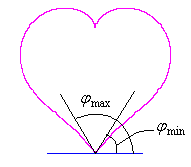
Method 1 is to make a heart curve from a Cardioid by forming an angle on its bottom simply, where the heart curve will be used as a petal of a flower, 2.1 In the case of no change in the length and width of heart curve to be used as a petal of flower
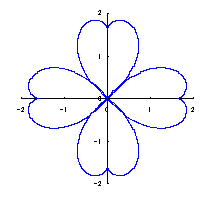
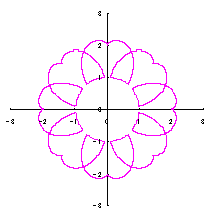
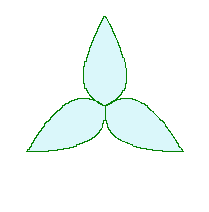
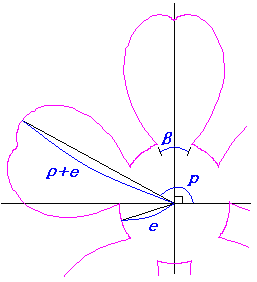
The original Cardioid is shown in Fig,1a, and the heart curve, which is produced from this original Cardioid by the method 1 as described in the page of "heart curves II", is shown in Fig.1b. We intend to form a shape of flower by arranging heart curves around a center circle as petals of a flower.
|
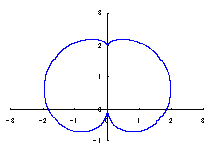
|
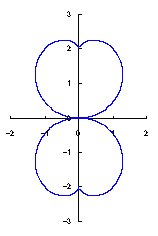
|
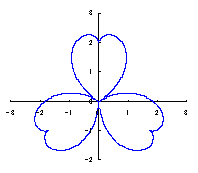
|
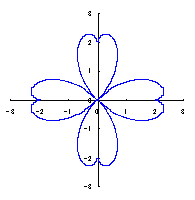
|
|
|
|
|
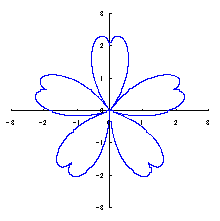
|
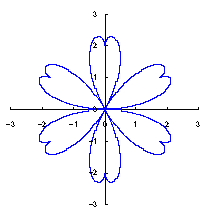
|
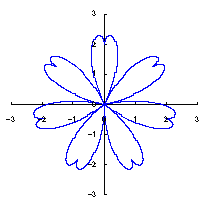
|
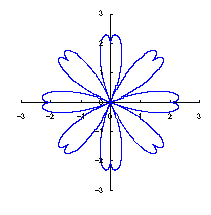
|
|
|
|
|
|
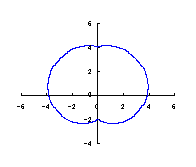 | 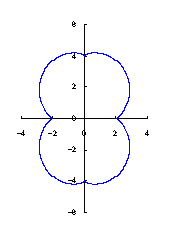 | 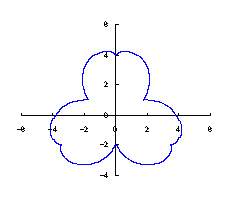 | 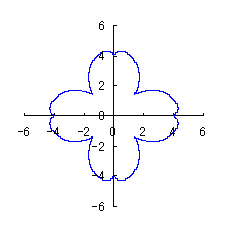 |
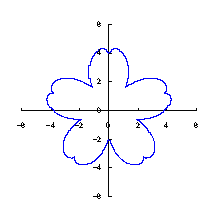 | 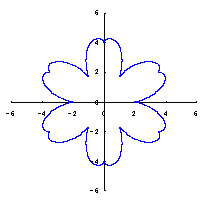 | 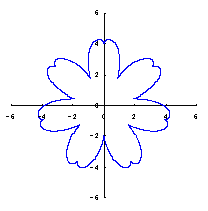 | 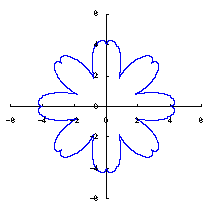 |
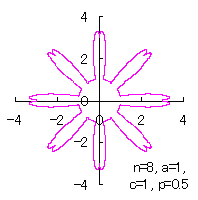 | 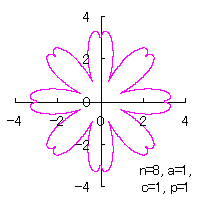 | 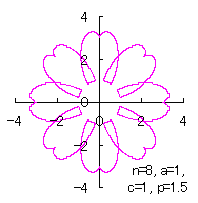 | 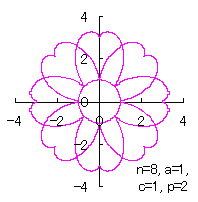 |  |
|
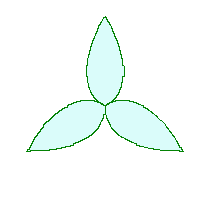
When the above figures are painted, the following ones are drawn.
    
| |
| Added in Sep 21, 2012. | |
|
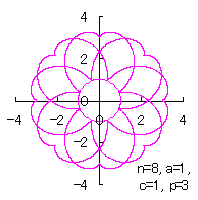
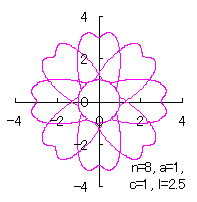
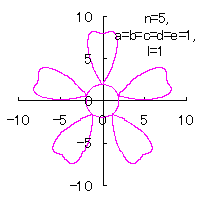
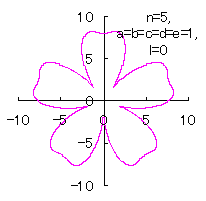
[2.1 Additional II] In the case that each petal contacts with the center circle with an arbitral width of phase angle of its circle
The base of petals may actually be connected to the flower floor with a narrow width. In the simulation of this page, this fact is corresponding to that the petals are connected to a center circle with a narrow width.
|
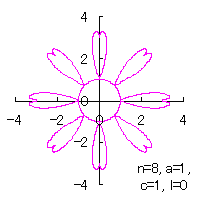 | 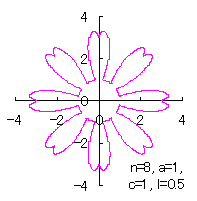 | 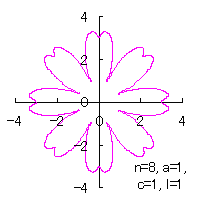 |  |
| |
| Added in Sep. 30, 2012. | |
|
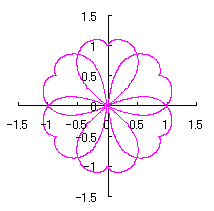
2.2 In the case of change in the length and width of heart curve to be used as a petal of flower
In this case, we return to a heart curve (as shown in Fig.1 and which is used as the material of a petal) in the (x, y) coordinate expression. This expression is described in the following two equations with |
 | 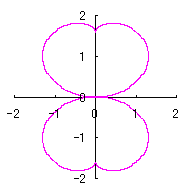 | 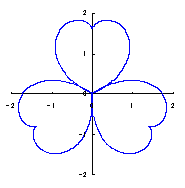 |  |
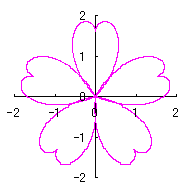 |  |  | 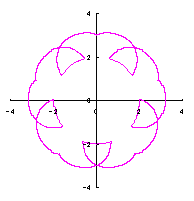 |
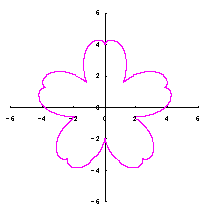 | 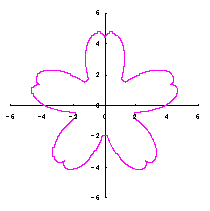 |  | 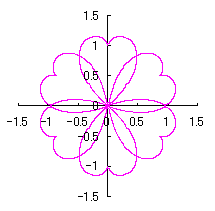 |
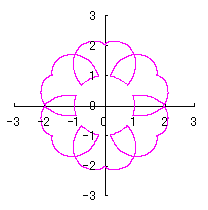 | 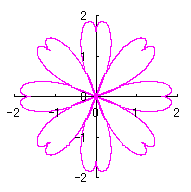 | 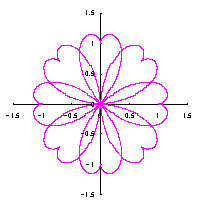 |  |
|
When the above figures are painted, the following ones are drawn. If clicked, an expanded line drawing appears.
               
[2.2 Additional I]
In the case of overlap among the petals of a flower
|
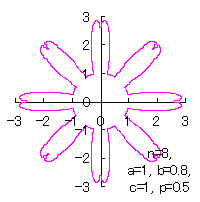 | 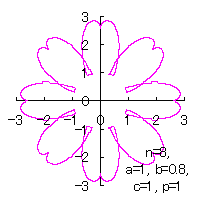 | 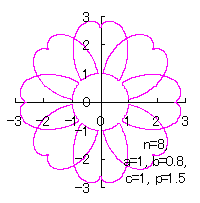 | 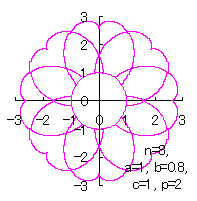 |
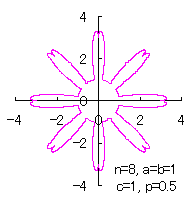 | 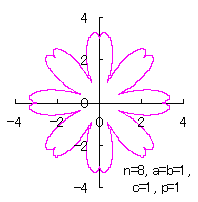 | 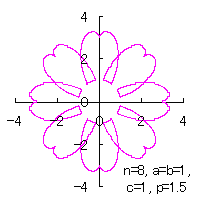 | 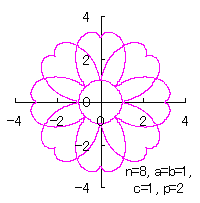 |
|
When the first half part of the above figures is painted, the following figures are drawn.
   
| |
| Added in Sep 21, 2012. | |
|
[2.2 Additional II]
In the case that each petal contacts with the center circle with an arbitral width of phase angle of its circle |
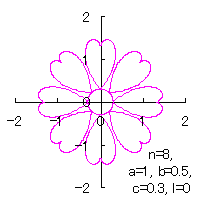 | 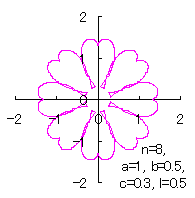 | 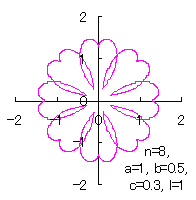 | 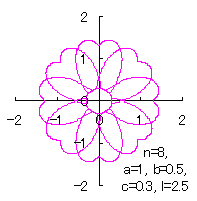 |
c=0.3, l=0 | c=0.3, l=0.5 | c=0.3, l=1 | c=0.3, l=2 |
| |
| Added in Oct. 01, 2012. | |
|
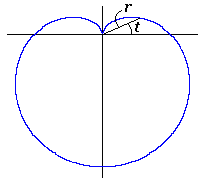
3. Method 2
Method 2 is to make a heart curve from a Cardioid by forming an angle on its bottom in application of some conversion equation of the phase angle, where the heart curve will be used as a petal of a flower,
|
 | 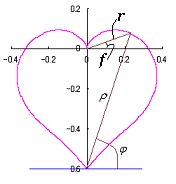 | 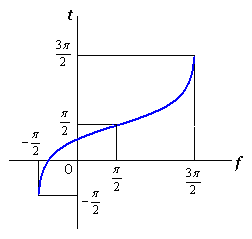 |
|
| from |
|
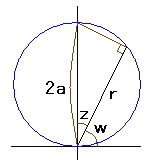
The equations obtained in the page "heart curves II" and used also in this page are the following three ones;
The origin point in Fig.31b is needed to be moved to the bottom of the heart curve. Although Eq.(16) is not varied in such a displacement, Eq.(17) should be varied in the following equation.
Newly, the expression of the whole shape of a flower in the orthogonal coordinates are given as
3.1.1 In the case using Fig.33
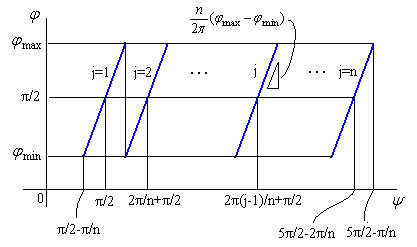
As seen in Fig.33, the minimum and maximum phase angles of the heart curve possess the proper meanings. The values of these angles will be obtained by software of C program. On this base, the (x, y) coordinate data of shape of flower are calculated by Eqs.(15) to (24). Examples of such calculated shape of flower in the case of |
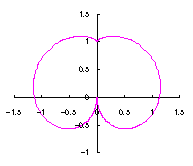 | 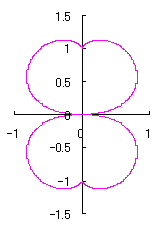 | 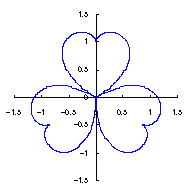 | 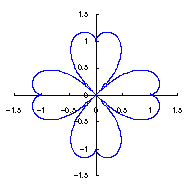 |
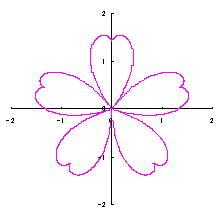 | 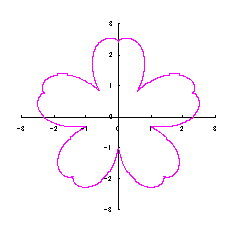 | 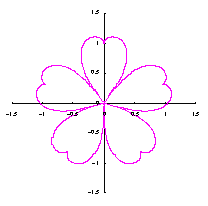 | 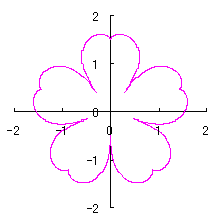 |
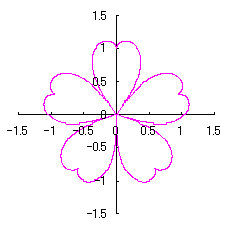 | 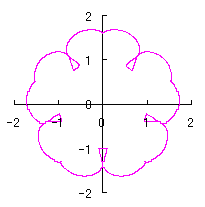 | 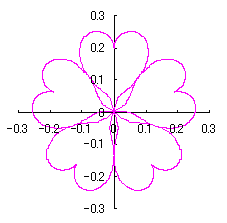 | 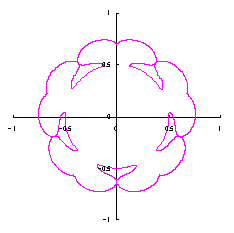 |
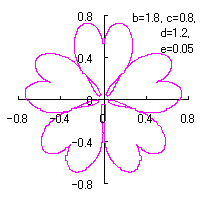 | 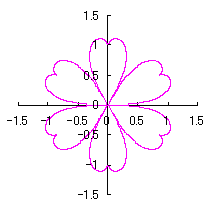 | 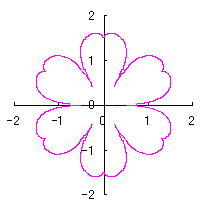 | 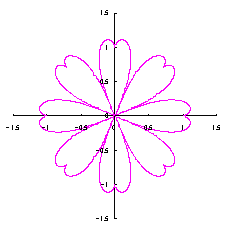 | 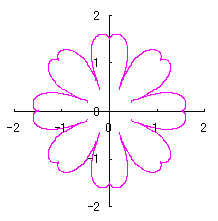 |
e=0.05 |
|
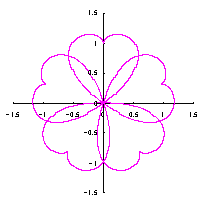
When the above figures are painted, the following ones are drawn. If clicked, an expanded line drawing appears.
                
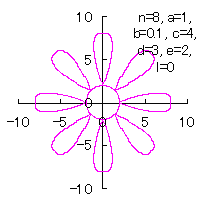
[3.1.1 Additional I] In the case of overlap among the petals of a flower In order to make overlap among the petals of a flower, it is prefered that the width of a single petal is intended to be increased. If the inclination of the lines in Fig.32 is increased, the width of a single petal is increased. Therefor, as the inclimentation factor 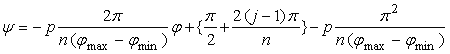 . (C1) . (C1)
Then, the (x, y) coordinate data of the shape of a flower are calculated by Eqs.(15) to (21), Eqs.(23), (24) and Eq.(C1), Examples of such calculated shape of flower in the case of |
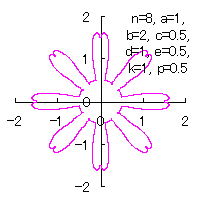 | 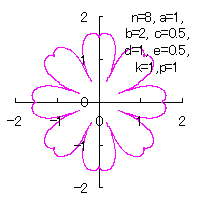 | 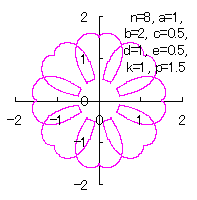 | 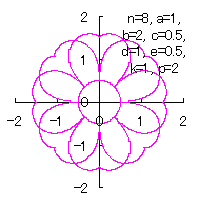 |
d=1, e=0.5, k=1, p=0.5 | d=1, e=0.5, k=1, p=1 | d=1, e=0.5, k=1, p=1.5 | d=1, e=0.5, k=1, p=2 |
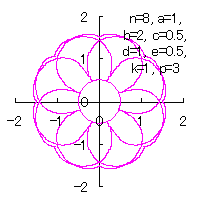 | 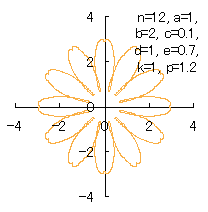 |
d=1, e=0.5, k=1, p=3 | d=1, e=0.7, k=1, p=1.2 |
|
When the above figures are painted, the following ones are drawn.
     
| |
| Added in Sep 22, 2012. | |
|
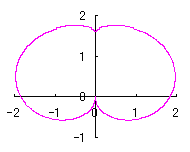
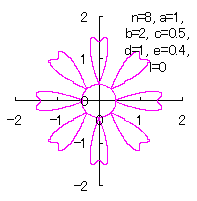
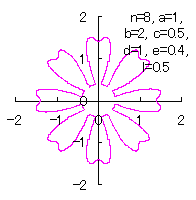
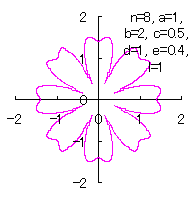
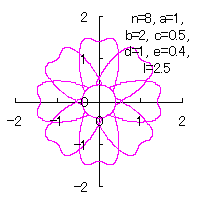
[3.1.1 Additional II] In the case that each petal contacts with the center circle with an arbitral width of phase angle of its circle
We can describe the solution of this problem as the followings likely as in [2.1 Additional II] of the section 2.1 and likely as in [2.2 Additional II] of the foregoing section.
|
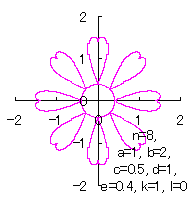 | 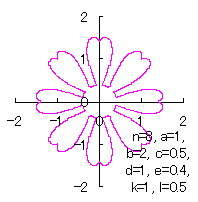 | 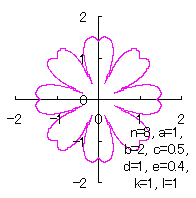 | 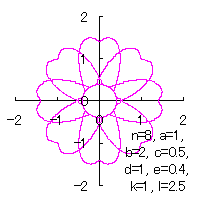 |
d=1, e=0.4, k=1, l=0 | d=1, e=0.4, k=1, l=0.5 | d=1, e=0.4, k=1, l=1 | d=1, e=0.4, k=1, l=2.5 |
| |
| Added in Oct. 01, 2012. | |
|
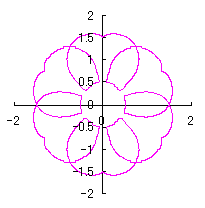
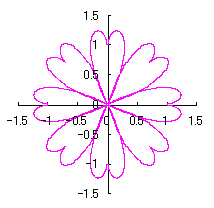
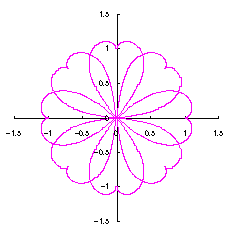
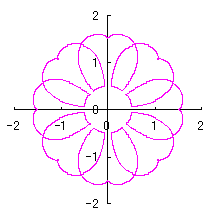
3.1.2 In the case using Fig.34
As seen in Fig.34, as the minimum and maximum phase angles are defined at the bottom of the heart curve, the values of these angles are generally different from ones described in the section 3.1.1. These angles are obtained analytically as
|
|
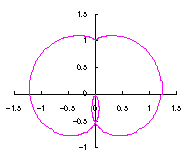 | 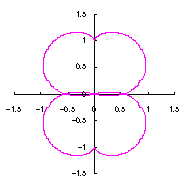 | 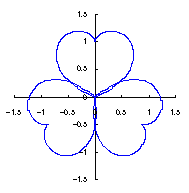 | 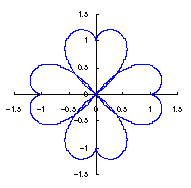 |
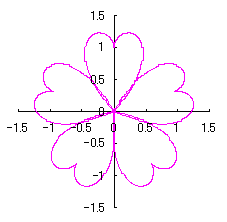 | 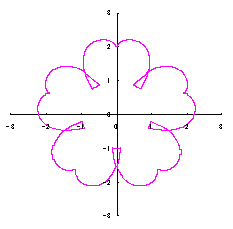 | 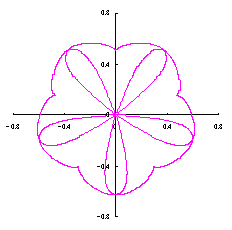 | 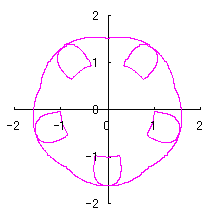 |
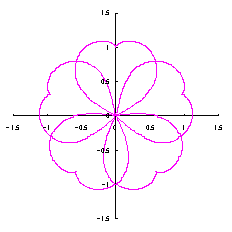 | 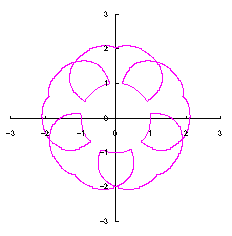 |  |  |
 |  |  |  |
When the above figures are painted, the following ones are drawn. If clicked, an expanded line drawing appears.               
[3.1.2 Additional I] In the case of overlap among the petals of a flower
We can use all the equations of Eqs.(15) to (21), Eqs.(23), (24) and Eq.(C1) as likely as used in the 3.1.1 Additional, |
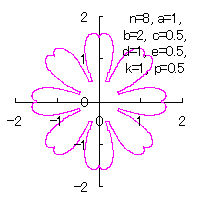 | 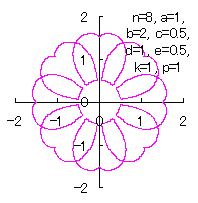 | 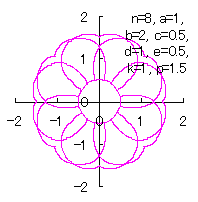 | 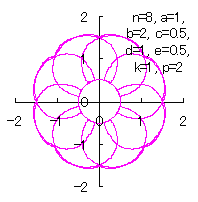 |
d=1, e=0.5, k=1, p=0.5 | d=1, e=0.5, k=1, p=1 | d=1, e=0.5, k=1, p=1.5 | d=1, e=0.5, k=1, p=2 |
|
When the above figures are painted, the following ones are drawn.
   
| |
| Added in Sep 22, 2012. | |
|
[3.1.2 Additional II] In the case that each petal contacts with the center circle with an arbitral width of phase angle of its circle
We can describe the solution of this problem as the followings likely as in [2.1 Additional II] of the section 2.1, likely as in [2.2 Additional II] of the the section 2.2 and likely as in [3.1.1 Additional II] of the foregoing section. |
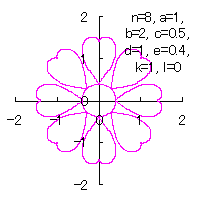 | 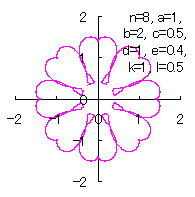 | 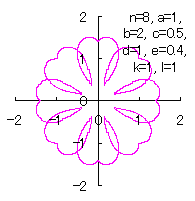 | 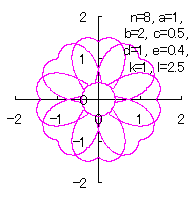 |
d=1, e=0.4, k=1, l=0 | d=1, e=0.4, k=1, l=0.5 | d=1, e=0.4, k=1, l=1 | d=1, e=0.4, k=1, l=2.5 |
| |
| Added in Oct. 01, 2012. | |
|
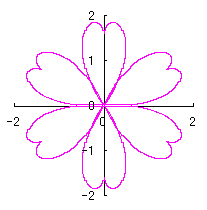
3.2 In the case of using heart curves as petals of a flower with simplification
The process treating in the previous section 3.1 is a little complicated for holding a correct shape of heart curve. So, we divert the phase angle |
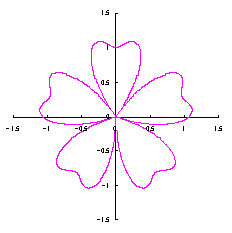 | 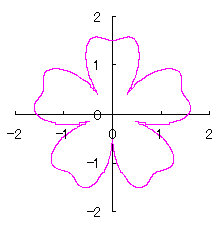 | 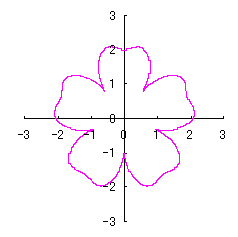 | 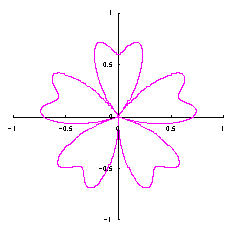 |
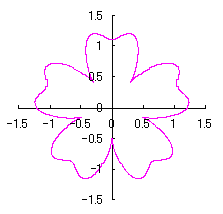 | 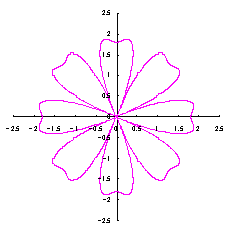 | 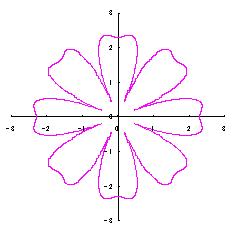 |
|
When the above figures are painted, the following ones are drawn. If clicked, an expanded line drawing appears.
[3.2 Additional I] In the case of overlap among the petals of a flower We can also use all the equations of From Eqs.(15) to (21) and Eq.(C1) as likely as used in the 3.1.1 Additional, Moreover, we use Eqs.(27) and (28) described just above. Then, the (x, y) coordinate data of the shape of a flower are calculated by Eqs.(15) to (21), Eq.(C1), Eqs.(27) and (28), Examples of such calculated shape of flower in the case of |
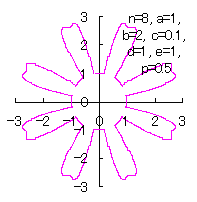 | 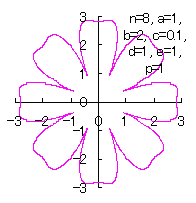 | 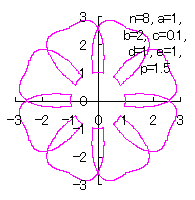 | 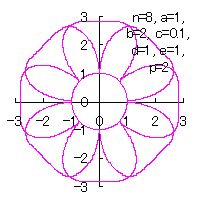 | 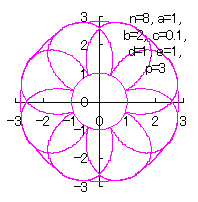 |
c=0.1, d=1, e=1, p=0.5 | c=0.1, d=1, e=1, p=1 | c=0.1, d=1, e=1, p=1.5 | c=0.1, d=1, e=1, p=2 | c=0.1, d=1, e=1, p=3 |
|
When the above figures are painted, the following ones are drawn.
    
| |
| Addid in Sep 22, 2012. | |
|
[3.2 Additional II] In the case that each petal contacts with the center circle with an arbitral width of phase angle of its circle
We can describe the solution of this problem as the followings likely as in [2.1 Additional II] of the section 2.1, likely as in [2.2 Additional II] of the the section 2.2 and likely as in [3.1.1 Additional II] of the foregoing section.
|
|
 |  |  |  |
c=0.5, d=1, e=0.4, l=0 | c=0.5, d=1, e=0.4, l=0.5 | c=0.5, d=1, e=0.4, l=1 | c=0.5, d=1, e=0.4, l=2.5 |
| |
| Added in Oct. 02, 2012. | |
|
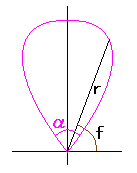
4. In the case of using Cardioid directly as a petal of flower
In this section, we treat the case of using Cardioid directly as a petal of flower.
4.1 In the case of no overlap among the petals of a flower
The conversion of the phase angle from |
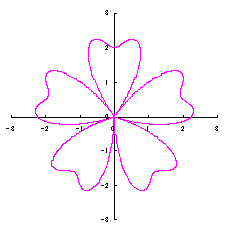 |
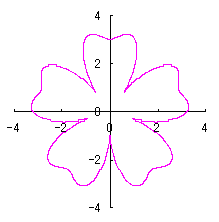 | 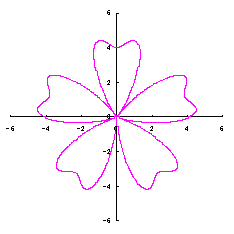 | 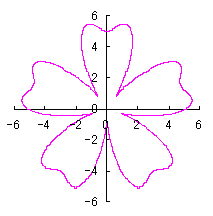 |
When the above figures are painted, the following ones are drawn. If clicked, an expanded line drawing appears.
   
4.2 In the case of overlap among the petals of a flower In this case, the conversion of the phase angle from 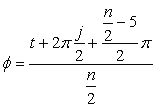 , (35-1) , (35-1)
where Further, as 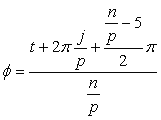 , (35-2) , (35-2)
where Calculating Eq.(18), Eqs.(29) to (33) and either Eq.(35-1) or Eq.(35-1), examples of shape of flower in the case of |
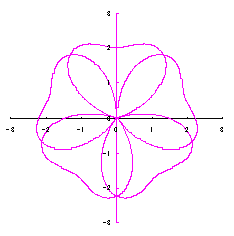 | 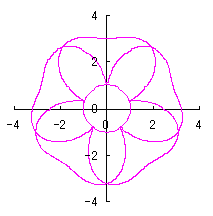 | 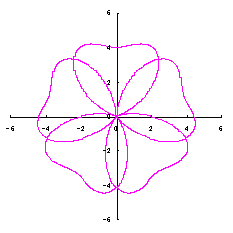 | 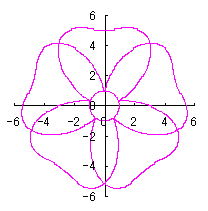 |
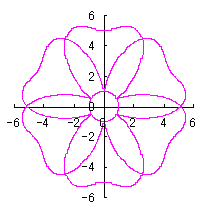 | 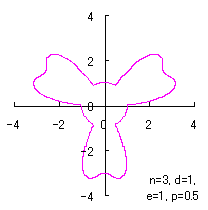 | 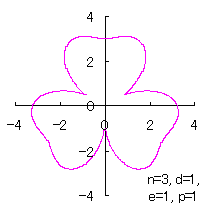 | 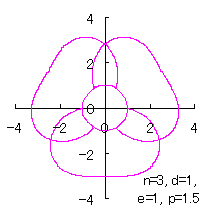 |
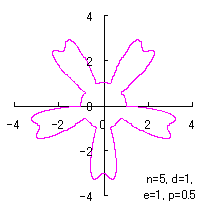 | 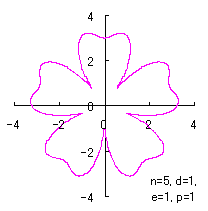 | 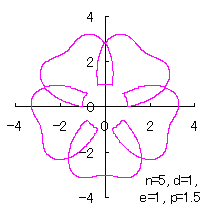 | 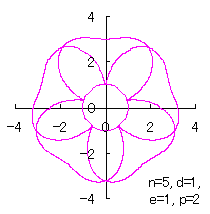 |
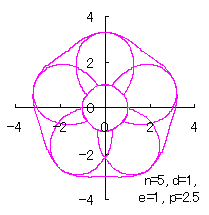 | 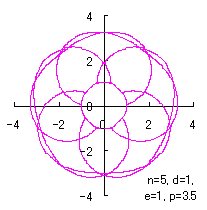 | 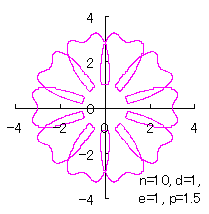 | 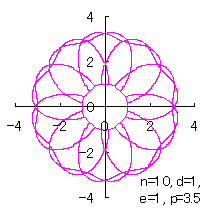 |
|
When the above figures are painted, the following ones are drawn. If clicked, a line drawing appears.
               
| |
| edited in Mar. 15, 2009 & reviced in Sep. 11, 2012 | |
|
4.3 In the case that each petal contacts with the center circle with an arbitral width of phase angle of its circle
We can also use Eq.(18) and Eqs.(29) to (33). |
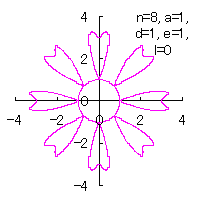 | 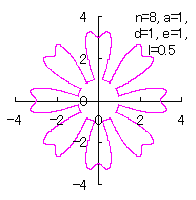 | 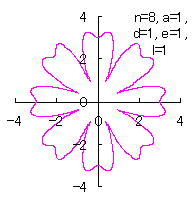 | 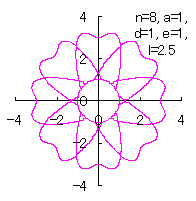 |
| |
| Added in Oct. 02, 2012. | |
|
5. In the case of using a circle directly as a petal of flower
5.1 The first deformation of a circle used as a petal
We assume a deformed circle given by the followings in the orthogonal coordinates;
|
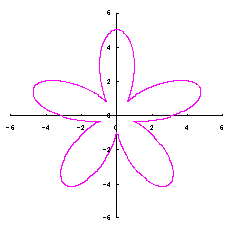 | 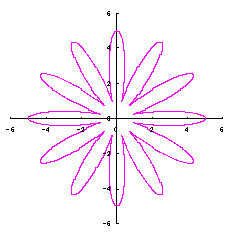 | 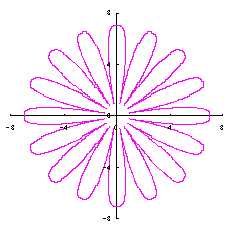 | 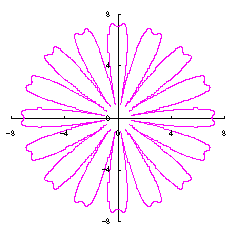 |
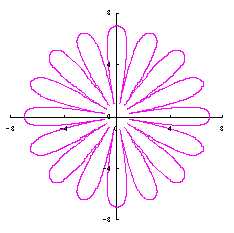 | 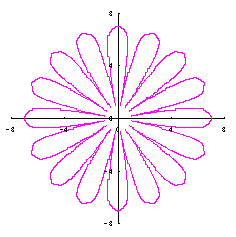 |  |
|
|
|
When the above figures are painted, the following ones are drawn. If clicked, an expanded line drawing appears.
      
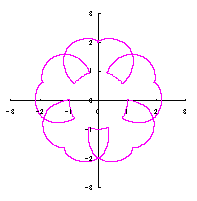
5.1.2 In the case of overlap among the petals of a flower
In this case, Eq.(35-1) or (35-2) can be used as the equation of transformation from |
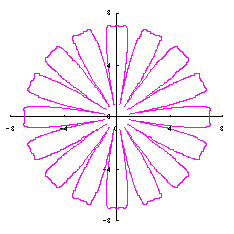
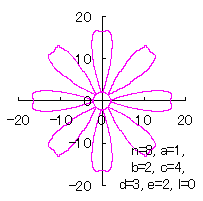
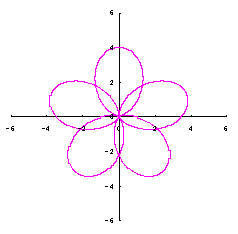 | 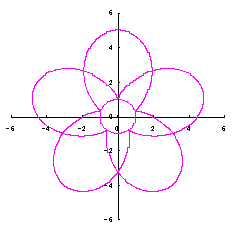 | 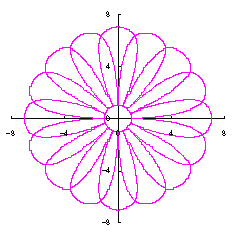 | 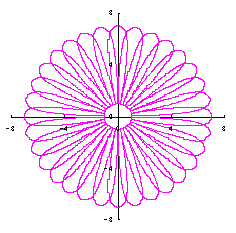 |
d=2, e=0, p=2 | d=2, e=1, p=2 | d=3, e=1, p=2 | d=3, e=1, p=2 |
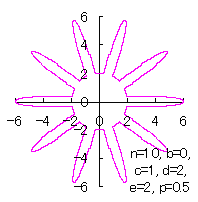 | 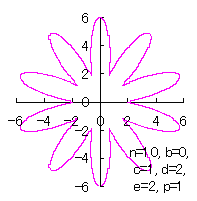 | 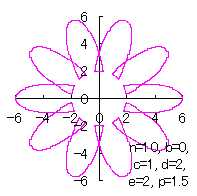 | 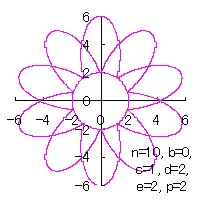 |
d=2, e=2, p=0.5 | d=2, e=2, p=1 | d=2, e=2, p=1.5 | d=2, e=2, p=2 |
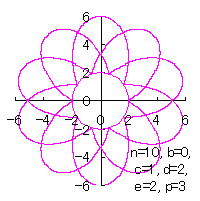 | 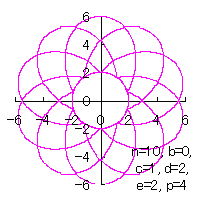 |
d=2, e=2, p=3 | d=2, e=2, p=4 |
|
When the above figures of Figs.85 to 83b and Fig.96f are painted, they are drawn as in the folloings. If the each of four figures in the left side is clicked, an expanded line drawing appears.
    
| |
| edited in Mar. 15, 2009 & reviced in Sep. 14, 2012 | |
|
5.1.3 In the case that each petal contacts with the center circle with an arbitral width of phase angle of its circle
We can also use Eqs.(27), (31), (36) and (37). |
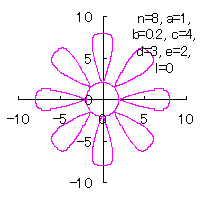 | 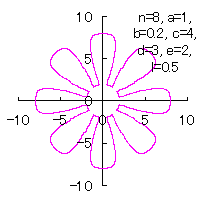 | 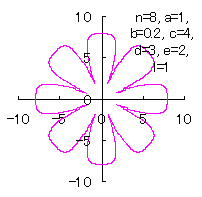 | 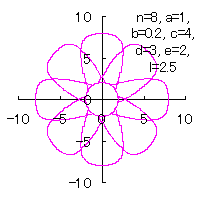 |
d=3, e=2, l=0 | d=3, e=2, l=0.5 | d=3, e=2, l=1 | d=3, e=2, l=2.5 |
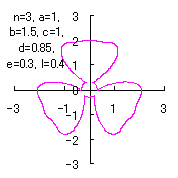 | 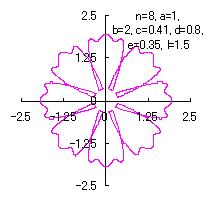 | 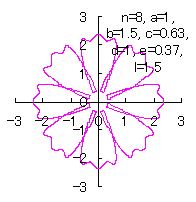 |
d=0.85, e=0.3, l=0.4 | d=0.8, e=0.35, l=1.5 | d=1, e=0.37, l=1.5 |
|
When the above figures of Fig.F1f and Fig.F1g are painted, they are drawn as in the folloings. If clicked, an expanded line drawing appears.
 
| |
| Added in Oct. 02, 2012. | |
|
5.1.4 The cases that the principal terms in Eqs.(36) and (37) are exchaneged mutually and/or the signs in Eqs.(36) and (37) are chaneged variously
We treat several cases that the principal terms in Eqs.(36) and (37) are exchanged mutually and /or the signs contained in Eqs.(36) and (37) are chaneged variously while process of calculations is obeyed to that described in the section 5.1.3. 5.1.4 (i) The case 1
The following two equations are proposed for replacing Eqs.(36) and (37). |
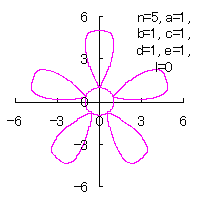 |
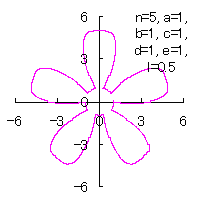 | 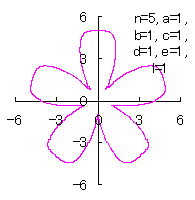 | 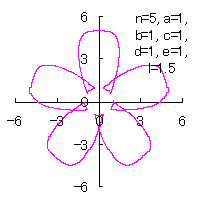 |
d=1, e=1, l=0 | d=1, e=1, l=0.5 | d=1, e=1, l=1 | d=1, e=1, l=1.5 |
| |
| Added in Oct. 16, 2012. | |
|
5.1.4 (ii) The case 2 The following two equations are proposed for replacing Eqs.(36) and (37). where the last term of Eq.(E4) is intended to move the origin to the bottom of the deformed circle. If the (x, y) coordinate data of the shape of a flower are calculated by Eqs.(E3), (E4), (31), (27), (D3) and (D4), some examples of figures in the case of |
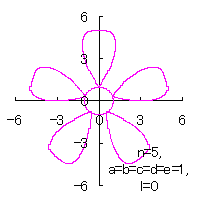 | 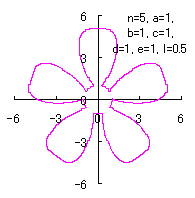 | 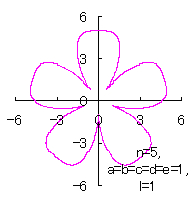 |
d=1, e=1, l=0 | d=1, e=1, l=0.5 | d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.1.4 (iii) The case 3
The following two equations are proposed for replacing Eqs.(36) and (37).
|
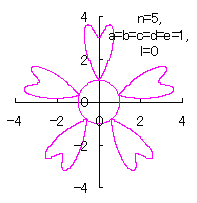 | 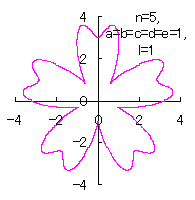 |
|
d=1, e=1, l=0 | d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.1.4 (iv) The case 4
The following two equations are proposed for replacing Eqs.(36) and (37).
|
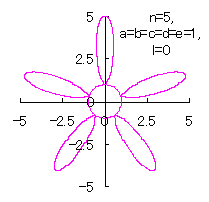 |  |
|
d=1, e=1, l=0 | d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.1.4 (v) The case 5
|
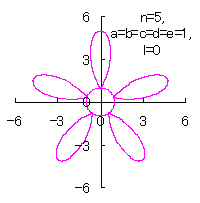 | 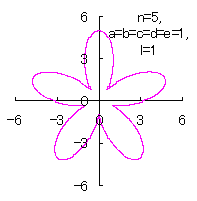 |
|
d=1, e=1, l=0 | d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
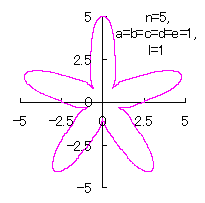
5.1.4 (vi) The case 6
|
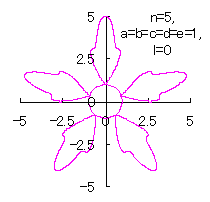 | 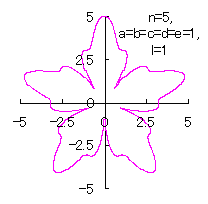 |
|
d=1, e=1, l=0 | d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.1.4 (vii) The case 7
|
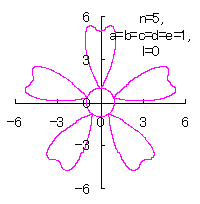 | 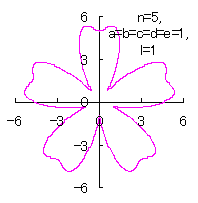 |
|
d=1, e=1, l=0 | d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.2 The second deformation of a circle used as a petal
Calculating Eqs.(31) to (34), Eqs.(38) and (39), examples of shape of flower in the case of |
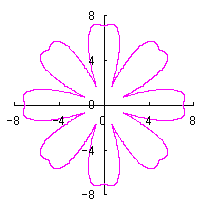 | 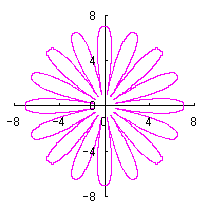 | 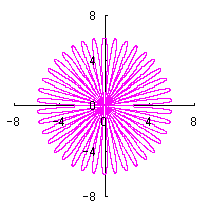 | 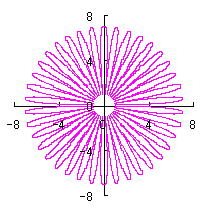 |
 |
|
|
|
|
|
|
|
When the above figures are painted, the following ones are drawn. If clicked, an expanded line drawing appears.     
| |
| A part of the figures and the picture are added in May 14, 2013. | |
|
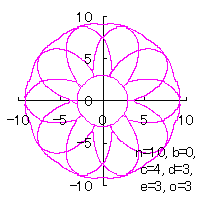
5.2.2 In the case of overlap among the petals of a flower As likely as in the previous section 5.1, Eq.(35-1) or (35-2) can be used as the equation of transformation from Calculating Eqs.(31) to (33), either Eq.(35-1) or (35-2), Eqs.(38) and (39), examples of shape of flower in the case of |
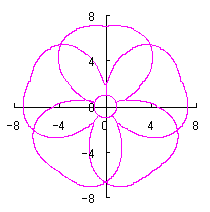 | 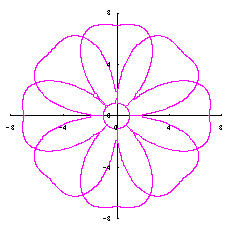 | 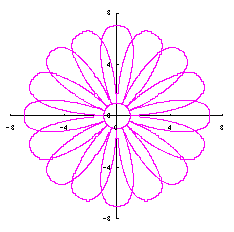 | 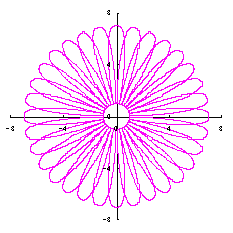 |
|
d=3, e=1, p=2 | d=3, e=1, p-2 |
d=3, e=1, p=2 |
d=3, e=1, p=2 |
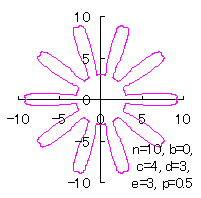 |
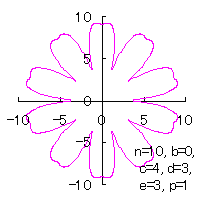 > > |
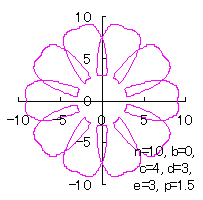 |  |
|
d=3, e=3, p=0.5 |
d=3, e=3, p=1 |
d=3, e=3, p=1.5 |
d=3, e=3, p=2 |
 |
 |
|
d=3, e=3, p=3 |
d=3, e=3, p=4 |
|
When the above figures Figs.89 to 91b and Fig.92f are painted, they are drawn as in the folloings. If the each of four figures in the middle is clicked, an expanded line drawing appears.
     
| |
| edited in Mar. 15, 2009 & reviced in Sep. 15, 2012 | |
|
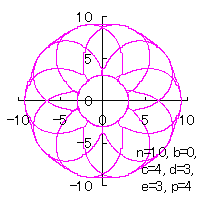
5.2.3 In the case that each petal contacts with the center circle with an arbitral width of phase angle of its circle
We can also use Eqs.(27), (31), (38) and (39). |
 | 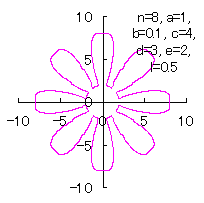 | 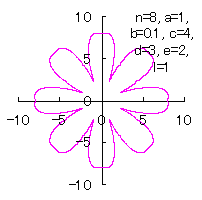 | 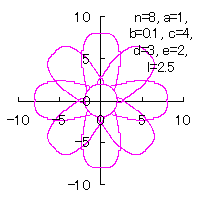 |
|
d=3, e=2, l=0 |
d=3, e=2, l=0.5 |
d=3, e=2, l=1 |
d=3, e=2, l=2.5 |
| |
| Added in Oct. 02, 2012. | |
|
5.2.4 The cases that the principal terms in Eqs.(38) and (39) are exchaneged mutually and/or the signs in Eqs.(38) and (39) are chaneged variously We treat several cases that the principal terms in Eqs.(38) and (39) are exchanged mutually and /or the signs contained in Eqs.(38) and (39) are chaneged variously while process of calculations is obeyed to that described in the section 5.2.3. 5.2.4 (i) The case 1
The following two equations are proposed for replacing Eqs.(38) and (39). |
 | 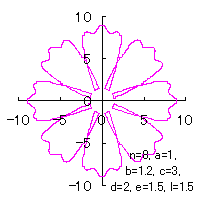 | 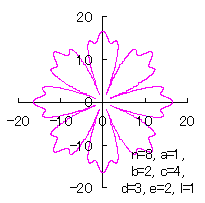 |
|
d=3, e=2, l=1.5 |
d=2, e=1.5, l=1.5 |
d=3, e=2, l=1 |
When the above figure >Fig.F2f is painted, it is drawn as shown in the folloing. If clicked, an expanded line drawing appears.

| |
| Added in Oct. 09, 2012. | |
|
5.2.4 (ii) The case 2
|
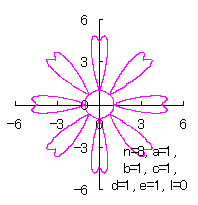 | 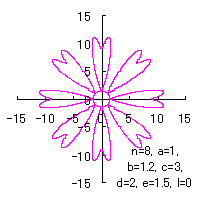 |  |
|
d=1, e=1, l=0 |
d=2, e=1.5, l=0 |
d=2, e=1.5, l=1.5 |
| |
| Added in Oct. 09, 2012. | |
|
5.2.4 (iii) The case 3 The following two equations are proposed for replacing Eqs.(38) and (39). where the last term of Eq.(F6) is intended to move the origin to the bottom of the deformed circle. If the (x, y) coordinate data of the shape of a flower are calculated by Eqs.(F5), (F6), (31), (27), (D3) and (D4), some examples of figures in the case of |
 |  | 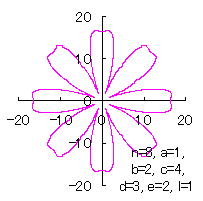 |
|
d=1, e=1, l=0 |
d=3, e=2, l=0 |
d=3, e=2, l=1 |
| |
| Added in Oct. 09, 2012. | |
|
5.2.4 (iv) The case 4
The following two equations are proposed for replacing Eqs.(38) and (39). |
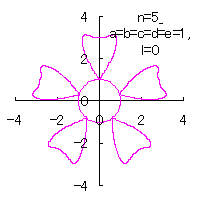 | 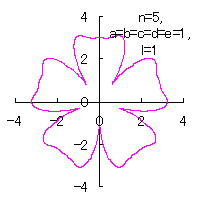 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.2.4 (v) The case 5
|
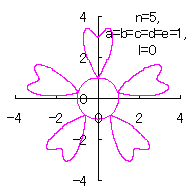 | 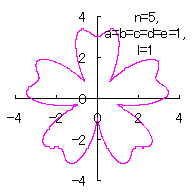 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.2.4 (vi) The case 6 The following two equations are proposed for replacing Eqs.(38) and (39). where the last term of Eq.(F12) is intended to move the origin to the bottom of the deformed circle. If the (x, y) coordinate data of the shape of a flower are calculated by Eqs.(F11), (F12), (31), (27), (D3) and (D4), some examples of figures in the case of |
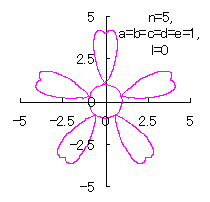 |
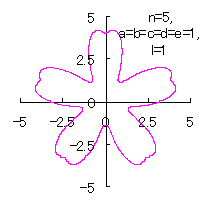 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.2.4 (vii) The case 7
The following two equations are proposed for replacing Eqs.(38) and (39).
|
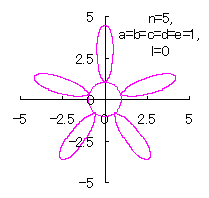 | 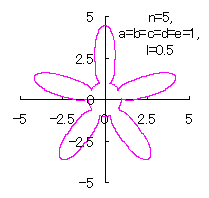 | 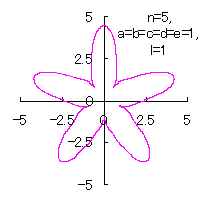 |
|
d=1, e=1, l=0 |
d=1, e=1, l=0.5 |
d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.3 The third deformation of a circle used as a petal
We assume a deformed circle given in the followings in the orthogonal coordinates;
|
 |  |  |
|
|
|
|
|
When the above figures are painted, the following ones are drawn. If clicked, an expanded line drawing appears.
  
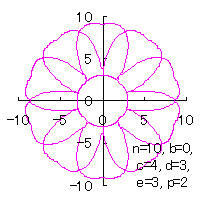
5.3.2 In the case of overlap among the petals of a flower As likely as in the previous sections 5.1 and 5.2, either Eq.(35-1) or (35-2) can be used as the equation of transformation from Calculating Eqs.(31) to (33), either Eq.(35-1) or (35-2), Eqs.(40) and (41), examples of shape of flower in the case of |
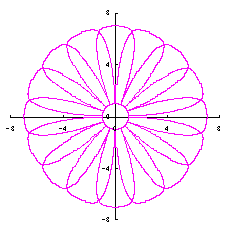 | 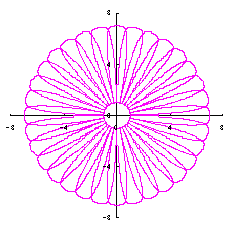 | 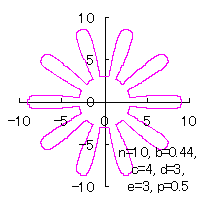 | 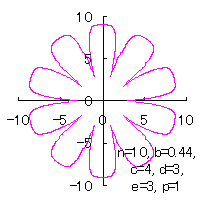 |
|
c=4, d=3, e=1, p=2 |
c=4, d=3, e=1, p=2 |
c=4, d=3, e=3, p=0.5 |
c=4, d=3, e=3, p=1 |
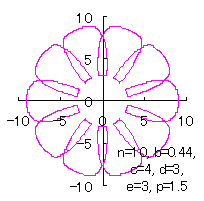 | 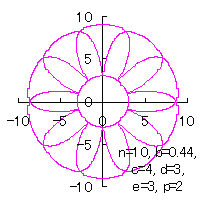 | 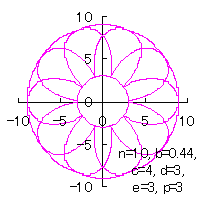 | 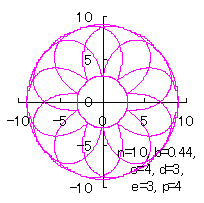 |
|
c=4, d=3, e=3, p=1.5 | c=4, d=3, e=3, p=2 |
c=4, d=3, e=3, p=3 |
c=4, d=3, e=3, p=4 |
|
When the above figures Figs.96a and b are painted, they are drawn as in the folloings. If the each of four figures in the left side is clicked, an expanded line drawing appears.
  
| |
| edited in Mar. 15, 2009 & reviced in Sep. 16, 2012 | |
|
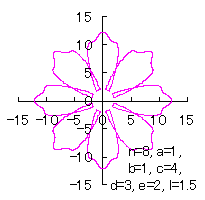
5.3.3 In the case that each petal contacts with the center circle with an arbitral width of phase angle of its circle We can also use Eqs.(27), (31), (40) and (41). Moreover, we can consider the solution of this problem as followgs likely as in [3.2 Additional II] of the section 3.2. So, we also use Eqs.(D3) and (D4). In calculating C program, we take the correction factor The (x, y) coordinate data of the shape of a flower are calculated by Eqs.(27), (31), (40), (41), Eqs.(D3) and (D4), Examples of such calculated shape of flower in the case of |
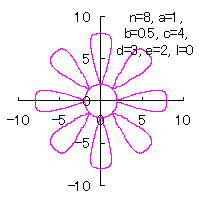 | 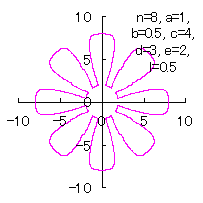 | 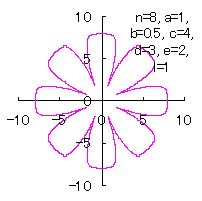 | 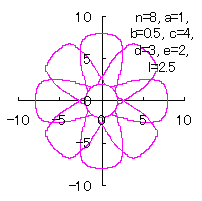 |
|
d=3, e=2, l=0 |
d=3, e=2, l=0.5 |
d=3, e=2, l=1 |
d=3, e=2, l=2.5 |
| |
| Added in Oct. 02, 2012. | |
|
5.3.4 The cases that the principal terms in Eqs.(40) and (41) are exchaneged mutually and/or the signs in Eqs.(40) and (41) are chaneged variously
We treat several cases that the principal terms in Eqs.(40) and (41) are exchanged mutually and /or the signs contained in Eqs.(40) and (41) are chaneged variously while process of calculations is obeyed to that described in the section 5.3.3.
|
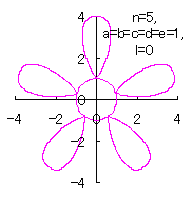 |
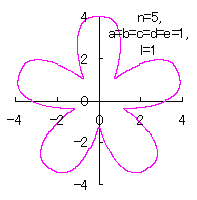 |
|
d=1, e=1, l=0 |
d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.3.4 (ii) The case 2
|
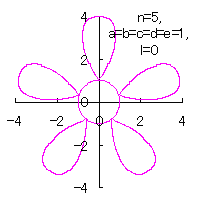 | 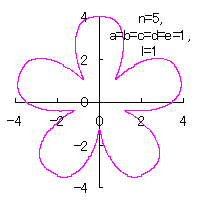 |
|
d=3, e=2, l=0 |
d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.3.4 (iii) The case 3
The following two equations are proposed for replacing Eqs.(40) and (41). |
 |  |
|
d=3, e=2, l=0 |
d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.3.4 (iv) The case 4
|
 |  |
|
d=3, e=2, l=0 |
d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.3.4 (v) The case 5
The following two equations are proposed for replacing Eqs.(40) and (41).
|
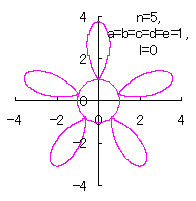 | 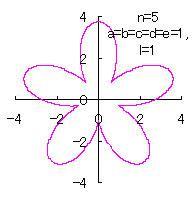 |
|
d=3, e=2, l=0 |
d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.3.4 (vi) The case 6
The following two equations are proposed for replacing Eqs.(40) and (41).
|
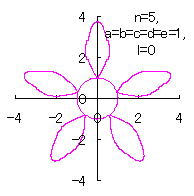 | 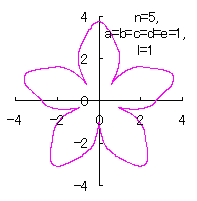 |
|
d=3, e=2, l=0 |
d=1, e=1, l=1 |
| |
| Added in Oct. 16, 2012. | |
|
5.3.4 (vii) The case 7
The following two equations are proposed for replacing Eqs.(40) and (41).
|
 | 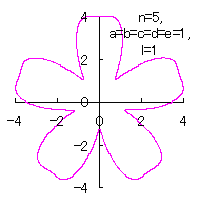 |
|
d=3, e=2, l=0 |
d=1, e=1, l=1 |
| |||||||||||
| Added in Oct. 16, 2012. | |||||||||||
|
6. Method to draw to set independently both of the phase angles of each petal and a center circle underlying each other
In the previous sections, a flower has been configured with the common phase angle of a center circle and its underlying each petal. In this manner, the width of the petal cannot be extended beyond the area of a predetermined phase angle of the center circle underlying.
The petal as shown in Fig.98b is created by sharpened the bottom of the circle as shown in Fig.98a. The equation of the circle in Fig.98a is described as
In the next, in order that the bottom of the circle is reformed into a petal curve with a corner having the desired angle (as seen in Fig.98b), we converse the phase angle 6.1.1 In the same case as in the previous sections in which common phase angle is applied to both of the each petal and the center circle underlying (reference for comparison)
In this case, the entire shape of a flower is expressed in the following two equations which are the same to Eqs.(6) and (7) in the section 2.1.
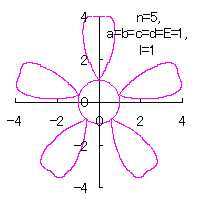
Calculating Eq.(42), either Eq.(48) or Eq.(48b), Eqs.(49), (50) and (51), an example of shape of flower in the case of
6.1.2 In the case that the phase angle of a center circle is set independently on the phase angle of each petal
According to how each petal contacts with the center circle, we will compose a flower graphics as divided into following three cases.
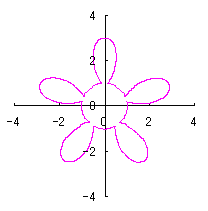
Calculating Eqs.(42), (48) or (48b), (49), (52) and (53), an example of shape of flower in the case of
6.1.2 (ii) In the case that each petal contacts with the center circle with an arbitral width of phase angle of its circle
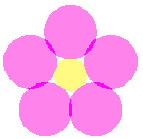
If we take |
 | 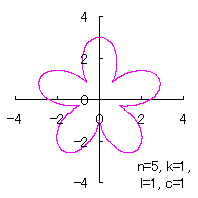 | 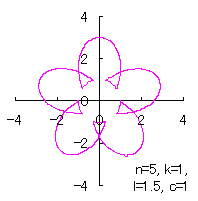 | 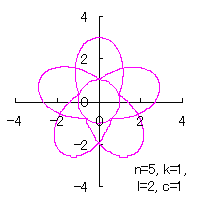 |
|
|
|
|
|
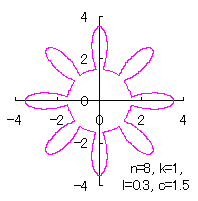 | 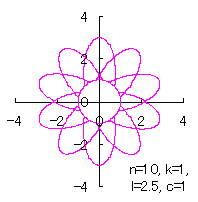 | 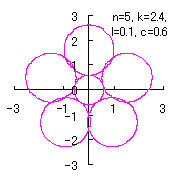 |  | |
|
|
|
|
6.1.2 (iii) In the case to sharpen the tip of the petal treated in the subsection 6.1.2 (ii)
|
| (If clicked, an expanded line drawing appears.) | |||
 |  |
 |
|
|
|
|
|
(If clicked, an expanded line drawing appears.) | |||
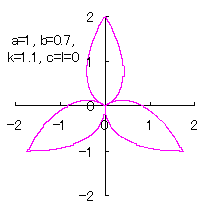 |
 |
|
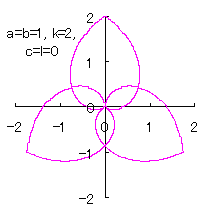 |
|
|
|
| |
| July 09, 2012 & Sep 09, 2012 | |
|
6.1.2 (iv) In the case to sharpen the tip of the petal treated in the subsection 6.1.2 (ii)...(part 2)
|
| (If clicked, an expanded line drawing appears.) | ||
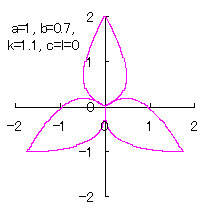 |  | |
|
|
| |||||||
| Sep 09, 2012 | |||||||
|
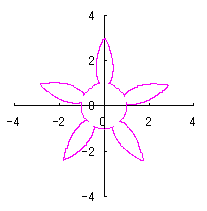
6.2 The case to configure the petals from cardioid There are two methods of the method 1 and 2 described in Section 2 and 3 respectively to convert the underlying heart curve in the form of a petal from cardioid. We will design a flower graphics according to the each method in case by case as below. 6.2.1 In the case with the use of the method 1 described in Section 2
We will treat a flower graphics along to "Method 1" described in Section 2. Unlike Section 2, we set independently of each other between the phase angle of petal and that of a center circle underlying. Therefore, though the following description may overlap with Section 2, its description is intended to be re-recorded for clarity.
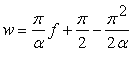 . (60) . (60)
If we substitute Eq.(59) into Eq.(60), the conversion equation from The orthogonal coordinate expression of the heart curve may be written as the following two equations; In order to broaden the variety in the form of a petal, we introduce In the next, we express the heart curve in the polar coordinates again. In this case, the moving radius We will arrange such the obtained heart curves as petals of a flower around a center circle of radius If the number
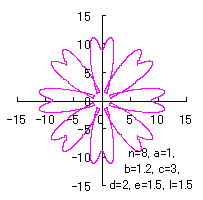
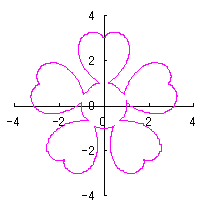
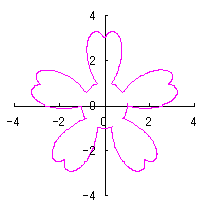
On theother hand, if we take |
 |  | 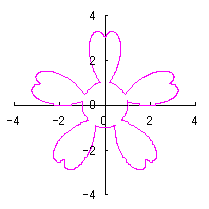 |  |
|
|
|
|
|
 | 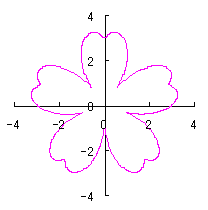 | 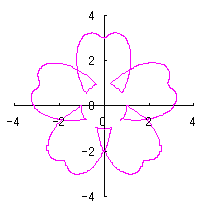 |
|
|
|
|
| |
| July 14, 2012 | |
|
6.2.2 In the case with the use of the method 2 described in the section 3
We will treat a flower graphics along to "Method 2" described in Section 3. Unlike Section 3, we set independently of each other between the phase angle of petal and that of a center circle underlying. Therefore, though the following discription may overlap with Section 3, its discription is intended to be re-recorded for clarity.
|
 |  | 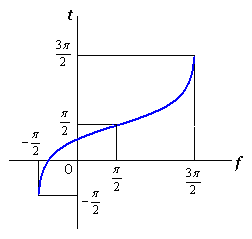 |
|
|
|
from |
|
Thus, the phase angle is converted as that the bottom of the cardioid becomes to sharpen.
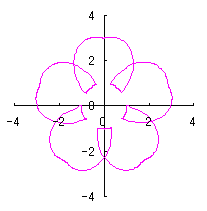
On the other hand, if we take |
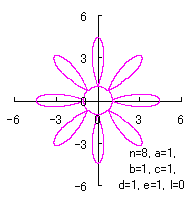
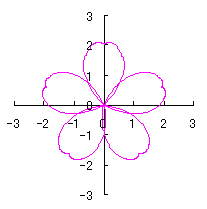 | 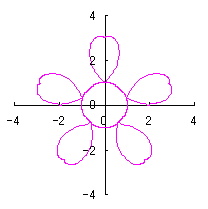 | 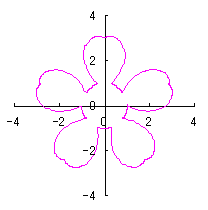 | 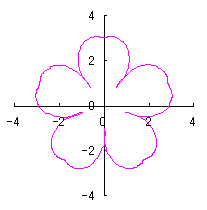 |
|
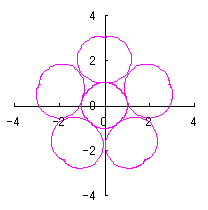
e=0, k=1, l=0 | e=1, k=1, l=0 | e=1, k=1, l=0.5 | e=1, k=1, l=1 |
 | 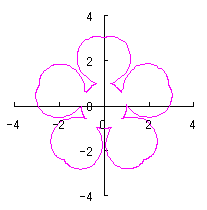 | 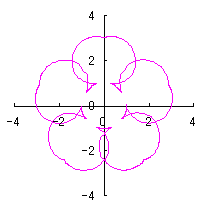 |  |
|
e=1, k=1, l=1.5 | e=1, k=1.5, l=0.5 | e=1, k=2, l=0.5 | e=1, k=2, l=0 |
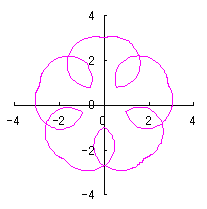 |  | 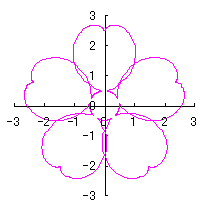 | 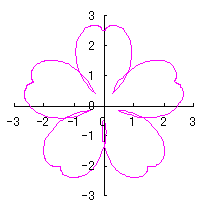 |
|
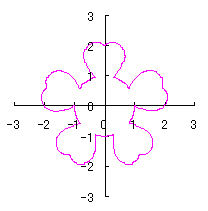
c=0, d=1, e=1, k=2, l=1 | e=1, k=2, l=0.5 | e=0.5, k=1, l=0.3 | e=0.5, k=0.7, l=1 |
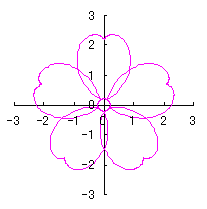 | 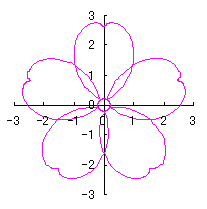 | 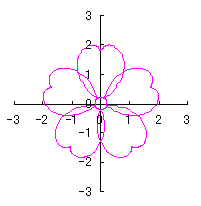 | 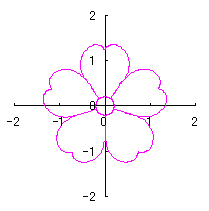 |
|
d=1, e=0.2, k=0.8, l=1 | d=1, e=0.2, k=0.8, l=1 | d=1, e=0.2, k=0.8, l=1 | d=1, e=0.2, k=1.5, l=1 |
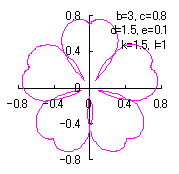 | 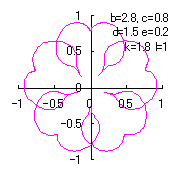 | 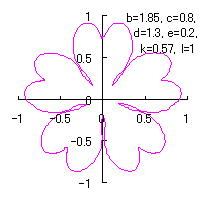 |
|
d=1.5, e=0.1, k=1.5, l=1 | d=1.5, e=0.2, k=1.8, l=1 | d=1.5, e=0.2, k=0.6, l=1 |
|
When Figs.127, 128 and 132d are painted, the following figures are drawn. If clicked, an expanded line drawing appears.
  
| |
| July 18, 2012 and May 14, 2013. | |
|
6.2.3 Deformation of the previous subsection 6.2.2
|
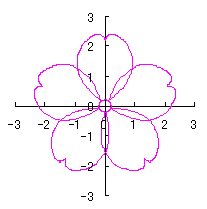 | 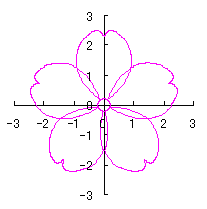 | 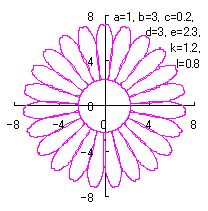 |
|
d=1.25, e=0.2, k=0.75, l=1 |
d=1.3, e=0.2, k=0.75, l=1 |
d=3, e=2.3, k=1.2, l=0.8 |
|
When the above figures are painted, the following ones are drawn. If clicked, a line drawing appears.
  
| |
| July 18, 2012 and May 09, 2013. | |
|
6.2.3 (ii) Deformation II of the previous section 6.2.2
The following equations are replaced to Eqs.(72a) and (72b) respectively in the previous section 6.2.2.
|
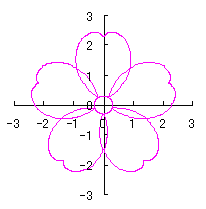 | 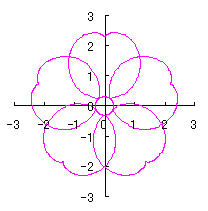 | 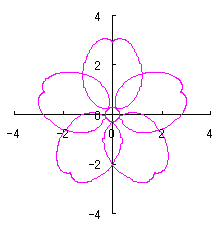 | 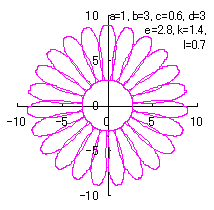 |
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
d=1.3, e=0.3, k=0.8, l=1 |
d=3, e=2.8, k=1.4, l=0.7 |
|
When Figs.135c and 136 are painted, the following figures are drawn. If clicked, an expanded line drawing appears.
 
| |
| July 22, 2012 and May 09, 2013. | |
|
6.2.3 (iii) Deformation III of the previous section 6.2.2
The following equations are replaced to Eqs.(72a) and (72b) respectively in the previous section 6.2.2. |
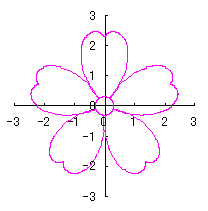 | 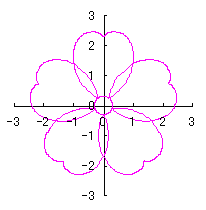 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
6.2.3 (iv) Deformation IV of the previous section 6.2.2 The following equations are replaced to Eqs.(72a) and (72b) respectively in the previous section 6.2.2. Calculating Eq.(71), Eqs.(73) to (80), Eqs.(84a) and (84b), examples of shape of flower in the case of |
|
(If clicked, an expanded line drawing appears.) | |||
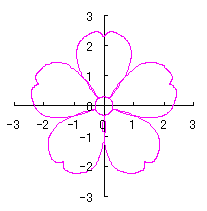 |
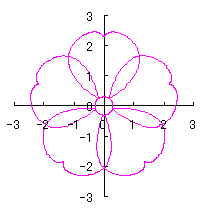 |
 |
|
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
6.2.3 (v) Deformation V of the previous section 6.2.2 The following equations are replaced to Eqs.(72a) and (72b) respectively in the previous section 6.2.2. Calculating Eq.(71), Eqs.(73) to (80), Eqs.(85a) and (85b), examples of shape of flower in the case of |
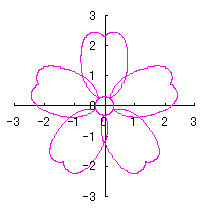 | 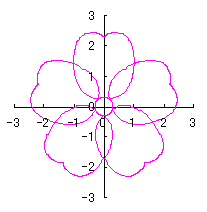 | 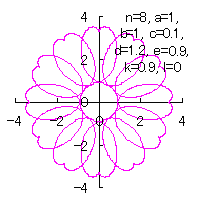 | 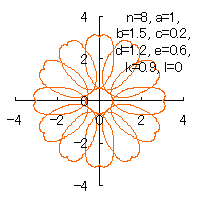 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
d=1.2, e=0.9, k=0.9, l=0 |
d=1.2, e=0.6, k=0.9, l=0 |
|
When the above figures Figs.142a and b are painted, they are drawn as in the folloings. If clicked, an expanded line drawing appears.
 
6.2.3 (vi) Deformation VI of the previous section 6.2.2 The following equation is replaced to Eq.(72a) in the previous section 6.2.2. Calculating Eq.(71), Eqs.(72b) to (80) and Eq.(86), examples of shape of flower in the case of |
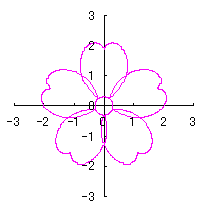 | 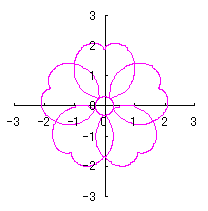 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
6.2.3 (vii) Deformation VII of the previous section 6.2.2
The following equation is replaced to Eq.(72b) in the previous section 6.2.2.
|
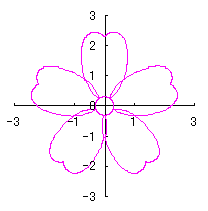 | 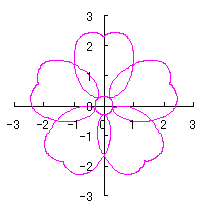 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
6.2.3 (viii) Deformation VIII of the previous section 6.2.2 The following equation is replaced to Eq.(72b) in the previous section 6.2.2.
|
| (If clicked, an expanded line drawing appears.) | ||||
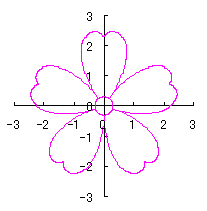 | 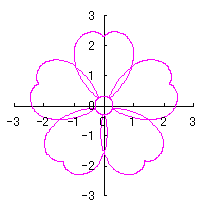 | 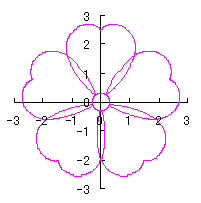 |  | |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
d=1.1, e=0.3, k=1.4, l=1 |
| |
| July 22, 2012 | |
|
6.2.3 (iX) Deformation IX of the previous section 6.2.2
The following equations are replaced to Eqs.(72a) and (72b) in the previous section 6.2.2.
|
| (If clicked, an expanded line drawing appears.) | ||||
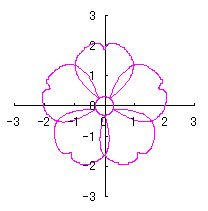 | 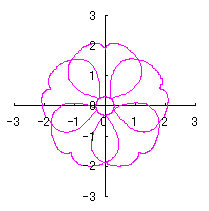 | 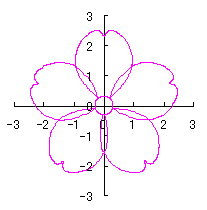 |  |
|
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
d=1.25, e=0.3, k=0.7, l=1 |
6.2.3 (x) Deformation X of the previous section 6.2.2
The following equations are replaced to Eqs.(72a) and (72b) in the previous section 6.2.2.
|
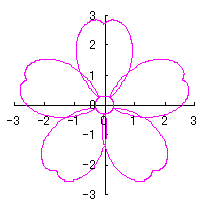 | 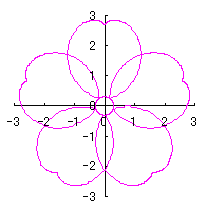 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
6.2.3 (xi) Deformation XI of the previous section 6.2.2 The following equations are replaced to Eqs.(72a) and (72b) in the previous section 6.2.2. 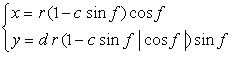 . (91) . (91)
Calculating Eq.(71), Eqs.(73) to (80) and Eq.(91), examples of shape of flower in the case of |
| (If clicked, an expanded line drawing appears.) | |||
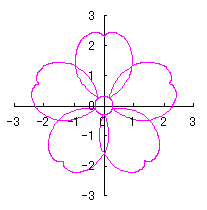 |  | 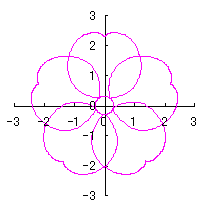 | |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
6.2.3 (xii) Deformation XII of the previous section 6.2.2 The following equations are replaced to Eqs.(72a) and (72b) in the previous section 6.2.2. 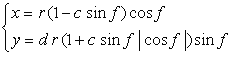 . (92) . (92)
Calculating Eq.(71), Eqs.(73) to (80) and Eq.(92), examples of shape of flower in the case of |
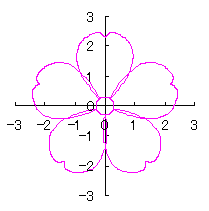 | 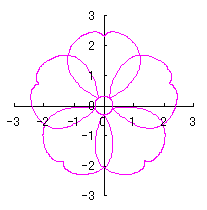 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
6.2.3 (xiii) Deformation XIII of the previous section 6.2.2
The following equations are replaced to Eqs.(72a) and (72b) in the previous section 6.2.2.
|
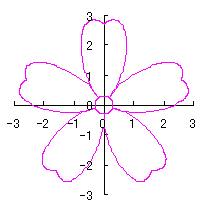 | 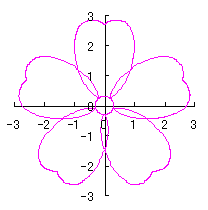 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
6.2.3 (xiv) Deformation XIV of the previous section 6.2.2 The following equations are replaced to Eqs.(72a) and (72b) in the previous section 6.2.2. 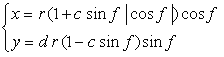 . (94) . (94)Calculating Eq.(71), Eqs.(73) to (80) and Eq.(94), examples of shape of flower in the case of |
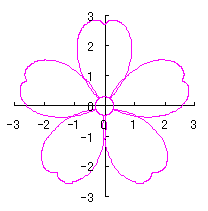 | 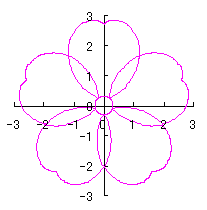 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
6.2.3 (xv) Deformation XV of the previous section 6.2.2
The following equations are replaced to Eqs.(72a) and (72b) in the previous section 6.2.2.
|
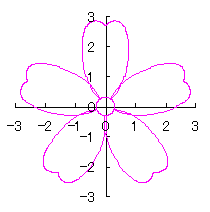 | 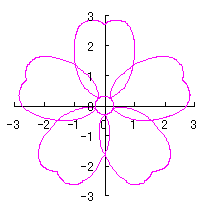 |
|
d=1, e=0.3, k=0.7, l=1 |
d=1, e=0.3, k=1, l=1 |
| |
| July 25, 2012 | |
|
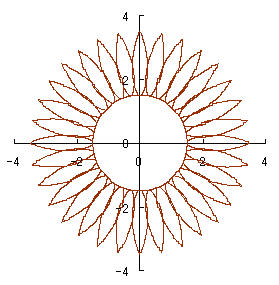
6.2.4 On the other deformation of the previous section 6.2.2
It may be considered that "the other function" is replaced into the function 6.2.4.a In the case of replacement of
Now, we suppose that the function |
| ||||||||||||||||||||||||||||||||||||||||||
|
|
| July 29, 2012 and Apr. 04, 2013 |
|
|
| May 15, 2013 | |
|
6.2.4.b In the case of replacement of
We suppose that the function
" y=d*r*(1-c*sin(f)*fabs(sin(f)))*sin(f)+2*a*d*(1+c); " to be replaced into " y=d*r*(1-c*sin(f)*fabs(sin(f)))*sin(f)+2*a*d; " in the C++ program of 6.2.3 (ii),
The results of the simulation by C++ program are obtained as shown in Figs.165(i), (ii), (iii), (iv), (v), (vi), (vii), (viii), (xi), (xii), (xiv) and (xv) according to the each method written in the subsections 6.2.3 (i), (ii), (iii), (iv), (v), (vi), (vii), (viii), (xi), (xii), (xiv) and (xv) respectively. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| July 31, 2012 and Apr. 02, 2013 |
| ||||||||||||
|
| ||||||||||||
| ||||||||||||
|
| ||||||||||||
| ||||||||||||
|
|
| Aug. 01, 2012 and Apr. 02, 2013 |
| ||||||||||||||||||
|
|
| Aug. 02, 2012 |
|
|||
| May 15, 2013 | |||
|
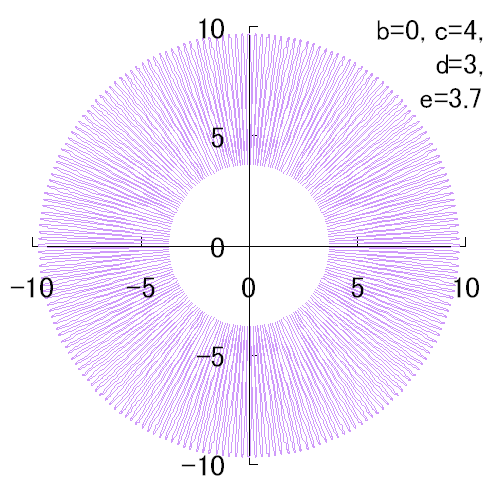
6.2.4.c Possibility of replacement of the other function into It is considered that the function such as 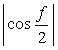 , , 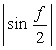 and etc. may also be replaced into the function and etc. may also be replaced into the function | |||
| July 31, 2012 | |||
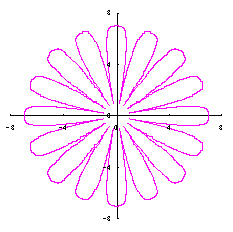
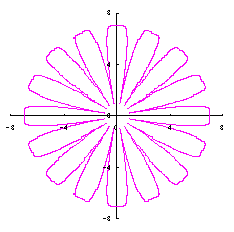
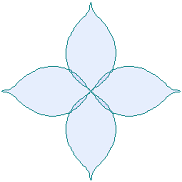
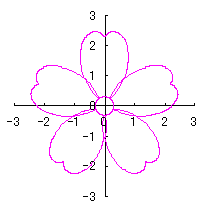
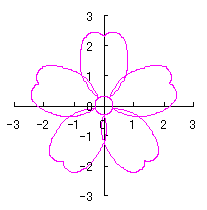
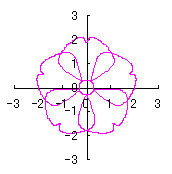
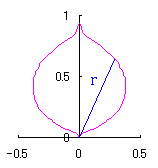
We find that the the simulation of the flower as described in the title is obtained by plotting as
|
|
(If clicked,
an expanded line drawing appears.) | |||
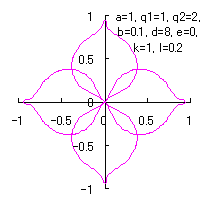 |
 |
|
|
|
d=8, e=0, k=1, l=0.2 |
|
(If clicked, an expanded line drawing appears.) | ||
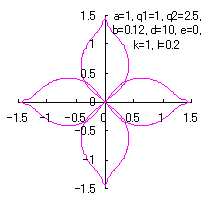 |
 |
|
|
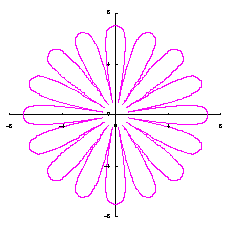
d=8, e=0, k=1, l=0.2 |
| |
| June 17, 2013 | |
_ returning to the page which opened just before with 'return' of browser _
or
_ returning to the HOME with the following button _
| HOME |
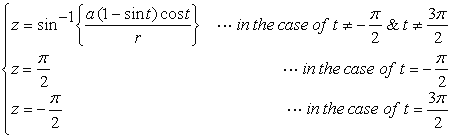 , (2)
, (2)

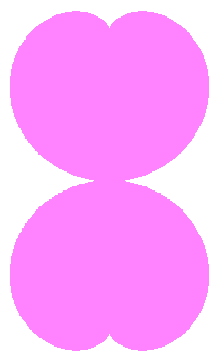















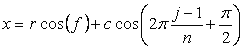 , (A2)
, (A2)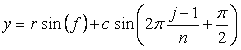 , (A3)
, (A3)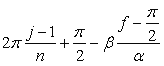 , and then, it depends on
, and then, it depends on 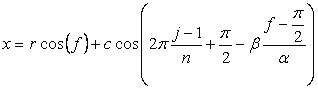 , (A4)
, (A4)
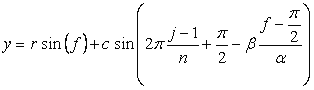 , (A5)
, (A5)
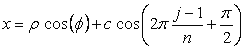 , (B2)
, (B2)
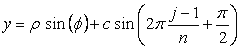 , (B3)
, (B3)
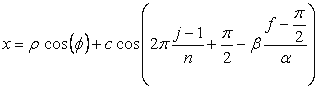 , (B4)
, (B4)
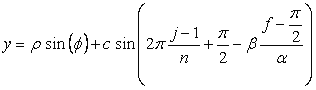 , (B5)
, (B5)
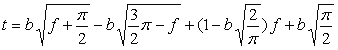 , (15)
, (15)
 . (21)
. (21)
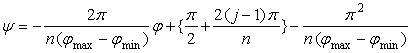 , (22)
, (22)

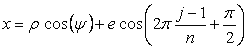 , (CI2)
, (CI2)
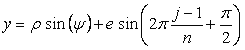 , (CI3)
, (CI3)
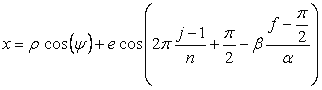 , (CI4)
, (CI4)
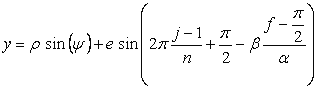 , (CI5)
, (CI5)
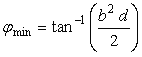 , (25)
, (25)
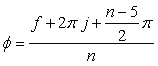 , (27)
, (27)







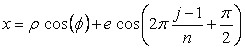 , (D1)
, (D1)
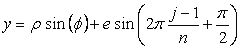 , (D2)
, (D2)
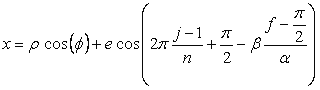 , (D3)
, (D3)
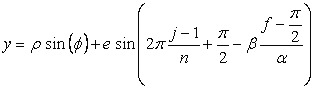 . (D4)
. (D4)
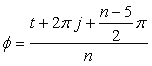 , (34)
, (34)
 are obtained as shown below.
are obtained as shown below.
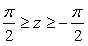 and
and 
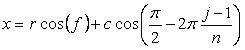 , (52)
, (52)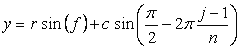 , (53)
, (53)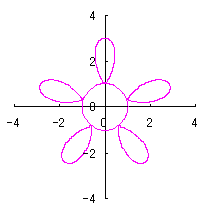
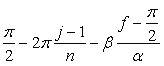 , and then, it depends on
, and then, it depends on 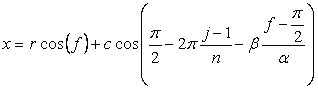 , (54)
, (54)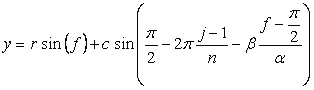 , (55)
, (55)
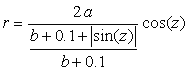 . (56-1)
. (56-1)
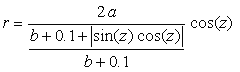 , (56-2)
, (56-2)
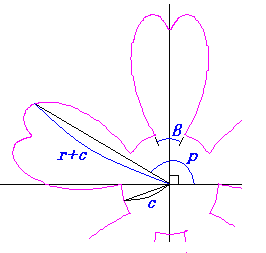
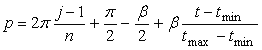 , (68)
, (68)
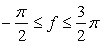 as shown in Fig.115c.
as shown in Fig.115c.
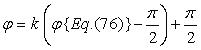 . (76b)
. (76b)
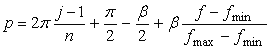 , (78)
, (78)
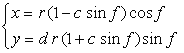 . (89)
. (89)
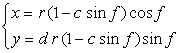 . (90)
. (90)
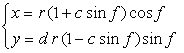 . (93)
. (93)
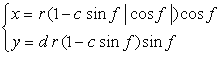 . (95)
. (95)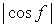 which is used in the previous subsections of 6.2.3 (i), (ii), (iii), (iv), (v), (vi), (vii), (viii), (xi), (xii), (xiv) and (xv) in the section 6.2.3.
By the way, as the function
which is used in the previous subsections of 6.2.3 (i), (ii), (iii), (iv), (v), (vi), (vii), (viii), (xi), (xii), (xiv) and (xv) in the section 6.2.3.
By the way, as the function 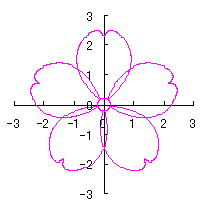
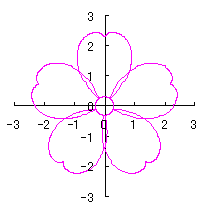
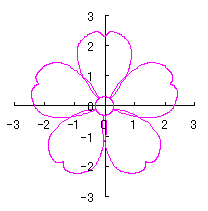
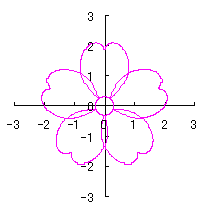
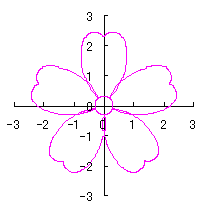
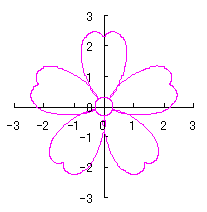
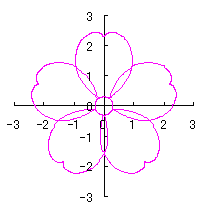

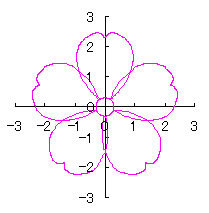
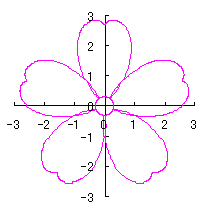
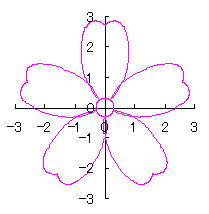
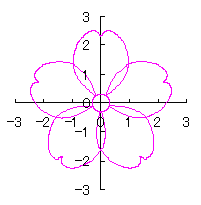
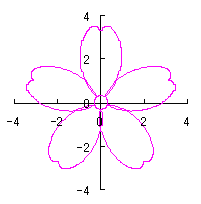
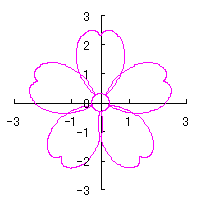
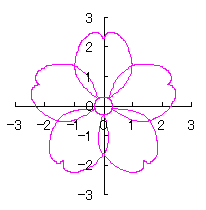

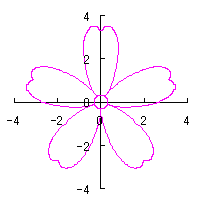
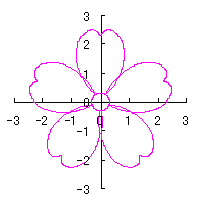
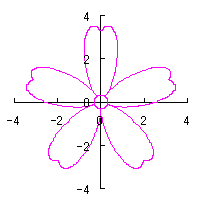
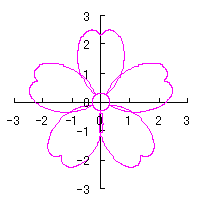
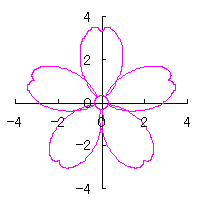
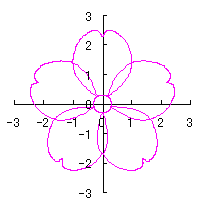

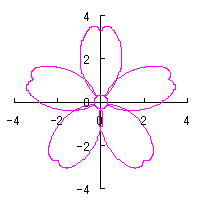
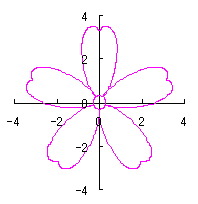
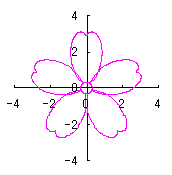
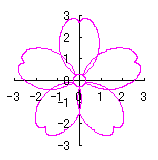

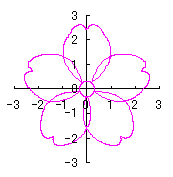

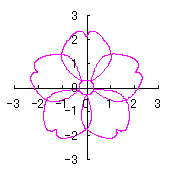

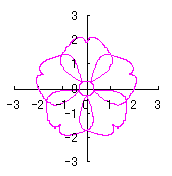
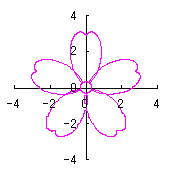
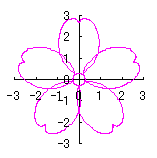
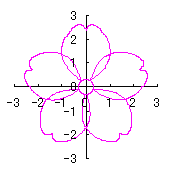

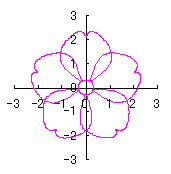
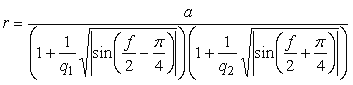 . (96a)
. (96a)
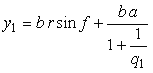 . (96c)
. (96c)
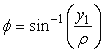 . (96e)
. (96e)
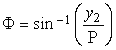 . (96i)
. (96i)
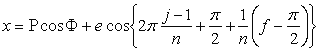 . (96j)
. (96j)
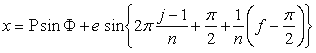 . (96k)
. (96k)