|
3. 「操作量(入力量)のピーク値低減化と応答の有限整定化(デッドビート化)との同時効果」
のための時間差比較補償法(TDCC 法)のブロック線図
「操作量(入力量)のピーク値低減化と応答の有限整定化(デッドビート化)との同時効果」
に用いる本補償器のブロック線図を図1に示す。サンプル時間 |
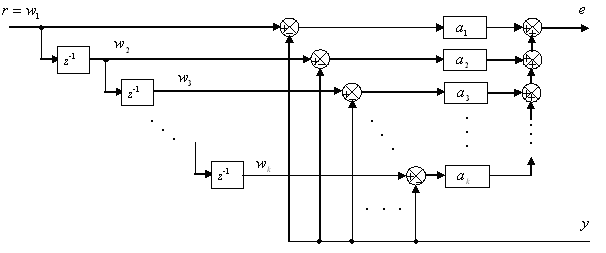
図1 ディジタルLQ最適制御における有限整定化と操作量ピーク値の低減化のための
時間差比較補償器(TDCC)のブロック線図は直接比較の配分率、
は各時間差比較の各配分率を示し、
は1サンプル時間の遅れ素子を示す。
|
4. 時間差比較補償法(TDCC 法)の「操作量(入力量)のピーク値低減化と応答の有限整定化
(デッドビート化)との同時効果」への応用例
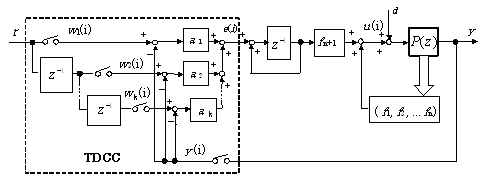
図2のように本補償器(TDCC)を搭載したLQ最適制御の帰還制御系を構成した場合を紹介する。
詳しくは、下記文献(1)、日本語では下記文献(2)
[←ここをクリックするとPDF化された論文が提示できます]および、下記文献(3)-(5)を参照されたい。
図2中、 |
|
| 図2 TDCC を用いたディジタル最適制御の構成 |
|
|
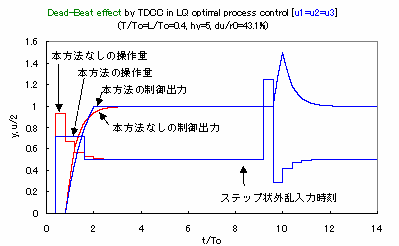
図3 図2のLQ最適制御系において、本方法による操作量の
ピーク値低減とステップ状目標値応答の有限整定化の同時効果 外乱応答には変化を来たさない。 |
|
5. 「操作量(入力量)のピーク値を低減化と、応答の有限整定化(デッドビート化)の同時効果」
に関する時間差比較補償法(TDCC法)の発表文献
(1) Nobuo YAMAMOTO, Michiya MASUDA, Akinori KAWAHARA, Takaya TANABE, and Makoto KIKUCHI: Dead-Beat Effect in LQ Optimal Control with the Use of Time- Difference Comparison Compensation", 茨城工業高等専門学校研究彙報,第41号,pp.31-38 (2006).
6. 追記
この研究に対して、アメリカの Journal of Systemics, Cybernetics and Informatics 学会 の the WMSCI 2005 組織委員会から、2005年6月10-13日にアメリカ・フロリダ州オーランドで開催される 「第9回システム、サイバーネティスク、および、情報の国際会議 [the 9th World Multi-Conference on Systemics, Cybernetics and Informatics (http://www.iiisci.org/sci2005)] 」への講演依頼の招待メール (こちら
|