|
To solve the form of seashore wave in hydrodynamic system is very difficult for the reason of a strong nonlinearity. Although the scientific accuracy is not expected, we try to simulate the form under simple assumption in this treatise.
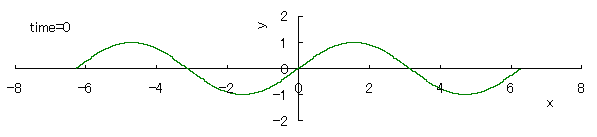
Even if a wave of surface of the sea in the offing is a sine wave, the phase velocity of the wave surface varies at the each point of height of the wave with the interaction with the viscosity and the countercurrent of the sea water as the wave approaches the coast.
Then, a wave crest appears, and soon, it collapses by gravity. We assume that a relative "difference" of the phase velocity in respect to the height y of the wave surface is given by two ways mentioned below.
In the each of the ways, we try to simulate the form of the wave which washes the beach.
Though such assumptions are ideally and unscientific, we introduce such obtained wave forms as these are interesting visually.
As a wave is transmitted to the coast from the offing, the phase velocity is decreased by influence of the viscosity mentioned above.
In another speaking, the wave length becomes short,
Attention must be paid to that the variation of the wave length does not appear apparently in this treatise as we will show the wave form in respect to the phase angle on the system moving at the phase velocity.
Moreover, a collapse in a wave crest by gravity is neglected for simplicity.
1. Method 1
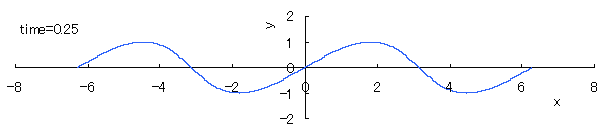
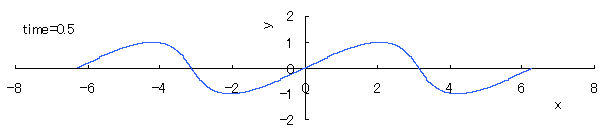
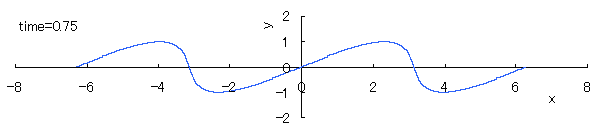
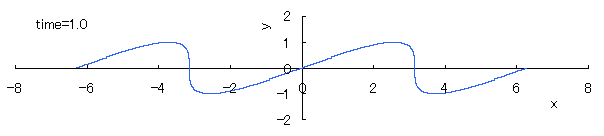
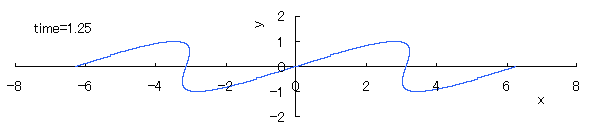
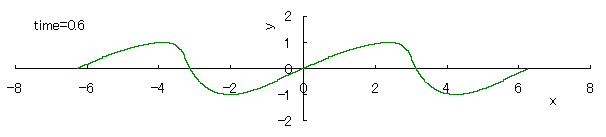
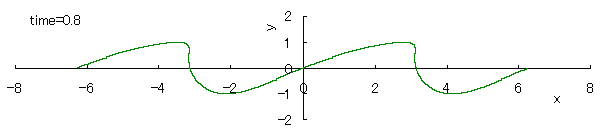
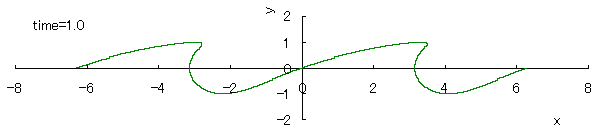
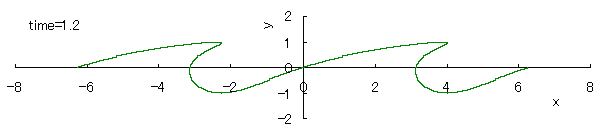
The relative "difference" of the phase velocity in respect to the height y of the wave surface is assumed to be proportional to y, and its magnitude is assumed to be constant in time. Then, the equation expressing the wave form y v.s. the phase angle x in each time is given as
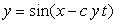 , (1) , (1)
where c indicates a degree in which the viscosity, the countercurrent and etc. have an influence to the relative difference of the phase velocity in respect to the height y of the wave surface.
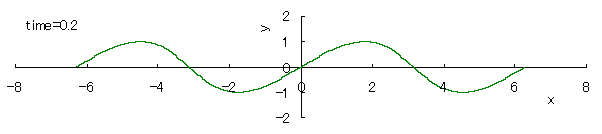
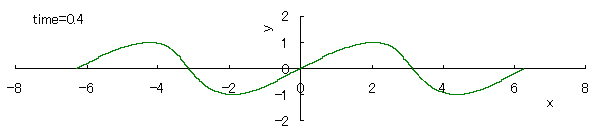
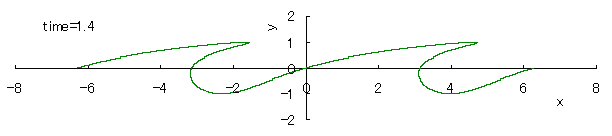
If we calculate Eq.(1) as varying the time with the use of computer in the case of c=1, the seashore wave forms are drawn as shown in the following.
However, as strictly known, these forms do not resemble to the real ones of seashore waves.
|