TDCC Laboratory
| HOME | JAPANESE |
Equation of Egg Shaped Curve VI
Nobuo YAMAMOTO
You can copy and use all the figures in this page freely.
|
This site is introduced in
GENERATING AVIAN EGG USING RATIONAL BEZIER QUADRATIC CURVES .
|
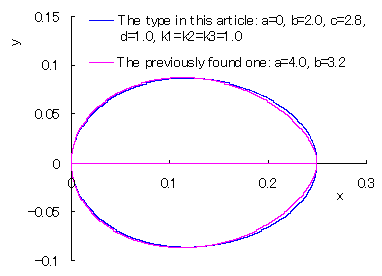
|
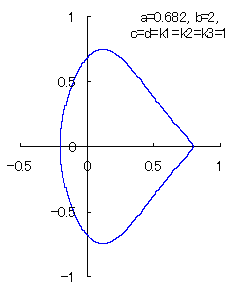
|
|
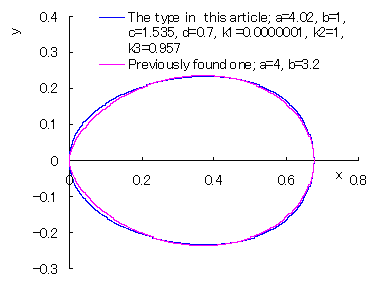
(The type in this article) and the previously founded one |
|
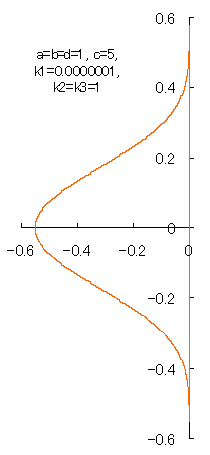
|
|
|
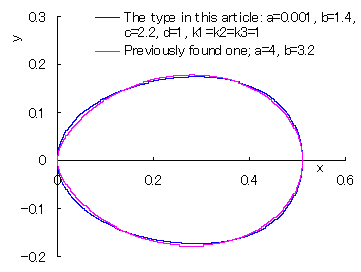
|
|
|
(The type in this article) and the previousely founded one |
|
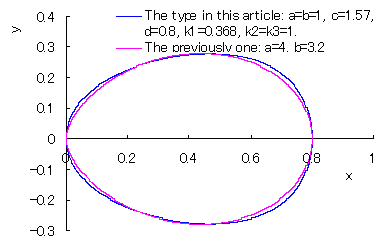
|
|
|
|
As an example, comparison between the curve in the case that a=0, b=1.5, c=2.2 and d=k1=k2=k3=1 and the shape of an actual egg is shown in Fig.8, where the values of the parameters a and b are a little changed from those in Fig.5. As seen in Fig.8, the egg shaped curve made from the equation of the convex distorded circle do not coincide to the shape of an actual egg so well.
|
_ returning to the page which opened just before with 'return' of browser _
or
_ returning to the HOME with the following button _
| HOME |