| HOME | JAPANESE |
Equation of Egg Shaped Curve of the Actual Egg is Found
Nobuo YAMAMOTO
You can copy and use all the figures except for Fig.2b in this page freely,
where Fig.2b is not created by the author of this page.
|
When we search for the internet about an oval curve, several sites of Egg Curves and Ovals, Oval and Cassini oval are found. But there seem to be little equations of a curve near a real egg shape. So, an equation of egg shaped curve which resembles closely to the shape of a chicken egg is pursued here apart from a mathematical definition of "oval curve".
|
|
1. Basic Derivation of Equation of Egg Shaped Curve
An equation of egg shaped curve (egg curve), which resembles to the shape of the actual egg more than Cassini oval etc. (continuing from the left), is obtained below.
In 2021, we received an inquiry about how to obtain Eq.(7). Certainly, the derivation of Eq. (7) does not seem to be so easy. Therefore, for reference, "the derivation of Eq. (7)" is shown. |
For simple expression of the above equation, we displace the trajectory by the value of |
|
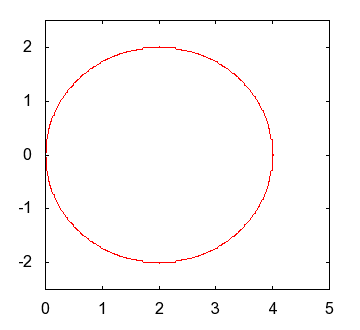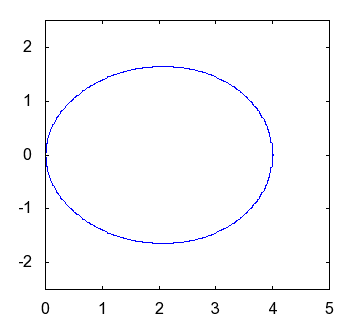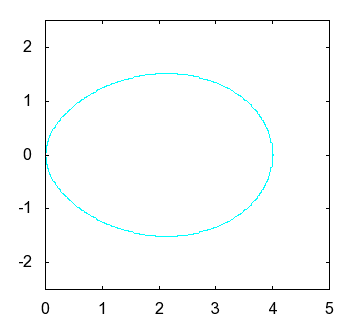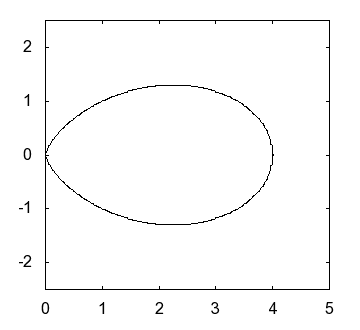
|
||
|
of and the shape of an actual egg |
|
If Eq.(9) is rewritten, the following equation is led into the expression indicating the obvious relation to this enveloping circle.
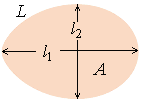
The major axis 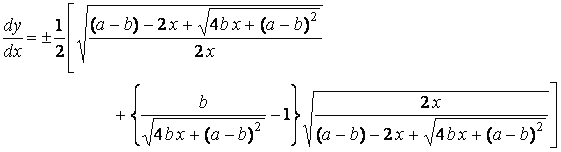 . (14b) . (14b)
In the next, the plane area
2. The Volume
and in the case of b=0, the volume of sphere having the radius a/2 is led to as As a reference, the calculation process of Eq.(15a) is written as 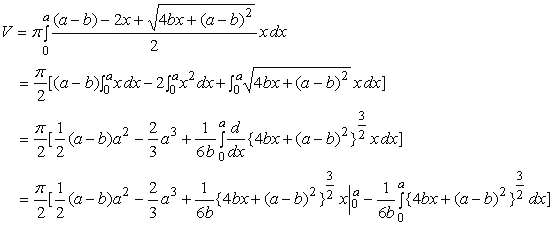 . (15b)' . (15b)'
In the next, the surface area 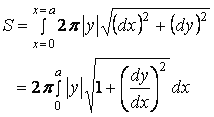 , (16) , (16)where More detail analyses are described in "How can I find the surface area of a normal chicken egg?".
|
Table 1 The volume
one round length
[Remark 1] The minor axis
So, its value will be obtained by computer calculation with C program.
[Remark 2] The nearest shape of egg to an actual egg exists arround
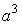 | ||||||||
|
Surface area of the egg shaped solid figure | 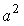 | 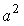 | 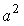 | 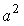 | ||||
|
| ||||||||
|
| ||||||||
|
egg shaped curve | ||||||||
|
egg shaped curve |
Especially, the relationship between the ratio
3. Expression of the Equations of the Egg Shaped Curves with the Use of the Intermediate Variable
return 4. The Case Using Ellipsoid instead of Circle as a Basic Figure
|
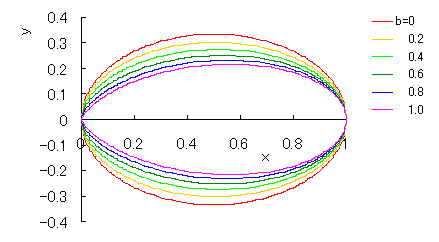
|
|
|
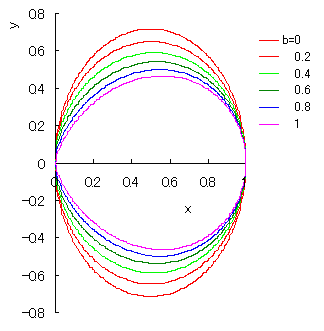
|
|
|
|
If we solve Eq.(20) with the usual method of the solution of the 2nd order equation, we obtain that return 5. The Case that the Constants "a" and/or "b" are/is out of the Defined Region
|
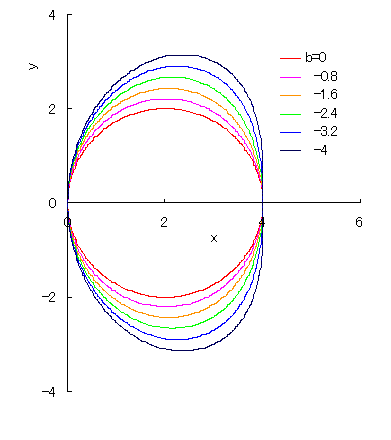
|
|
|
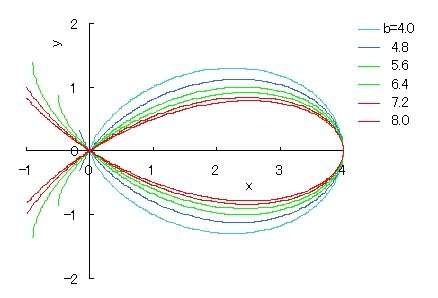
|
|
|
return 6. General Extension from Egg Shaped Curves to Pear Shaped Curves
|
|
where condition of constant c indicated in Eq.(10) is released for the reason of the extension, the conditions of d > 0 and f > 0 are needed for giving a closed curve, and new conditions which are explained in Eqs.(29) and (31) described below are added. Furthermore, the constant b is not used in this equation because the relation of |
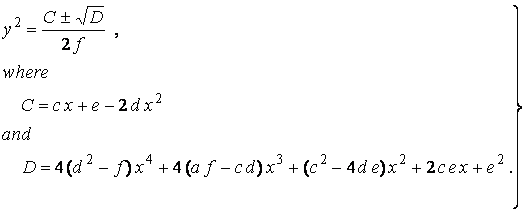 (25)
(25)
|
In the region of 0 < x< a in the above equation |
|
[Annotation] As a solution outside of 0 < x < a, the following equation also may exist besides Eq.(27). |
|
|
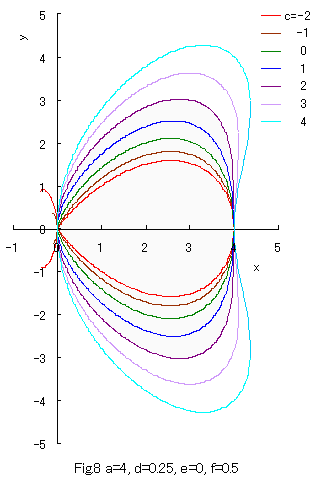
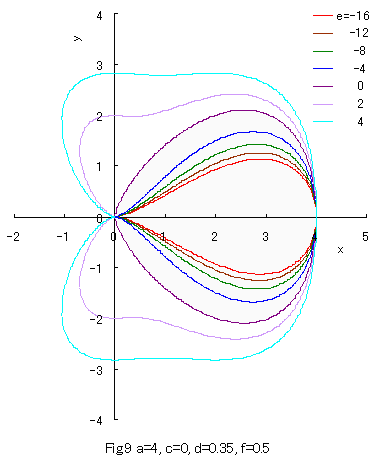
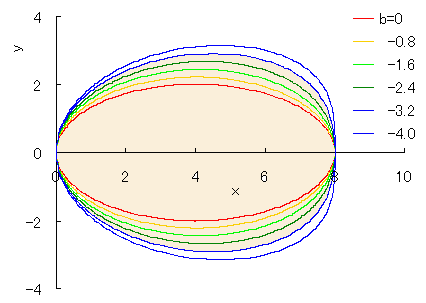
As seen in Fig.8, a closed curve goes out of the area of 0 < x < a when c > 2 whose condition does not satisfy Eq.(31). Moreover, as seen in Fig.9, a closed curve goes out of the area of 0 < x < a when e > 0 whose condition does not satisfy Eq.(29).
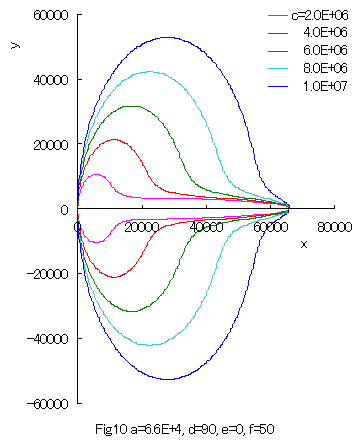
Furthermore, some interesting figures can be drawn as shown in Figs.10 and 11. |
 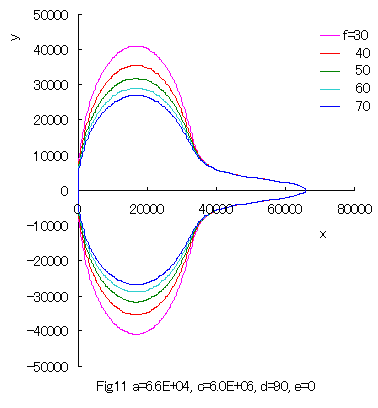 |
|
return
7. The Higher Order Equation I If we replace |
|
The solution of the above equation is given as |
|
Some examples of the curves which are given by Eq.(32) or its solution Eq.(33) are shown in Figs.12 and 13 in the region of |
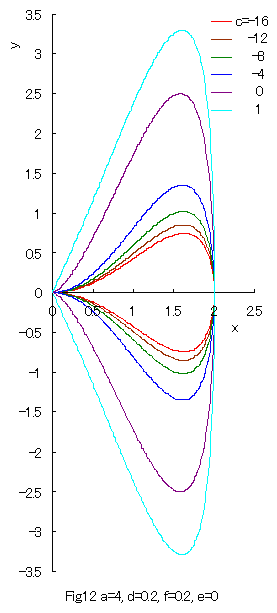 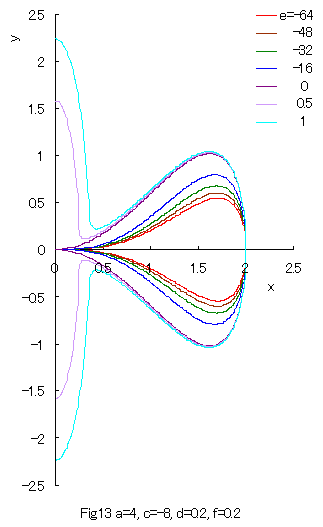 |
As seen in Fig.13, a closed curve does not exist within
Furthermore, some interesting figures can be drawn as shown in Figs.14 and 15 corresponding to Figs.10 and 11 respectively. |
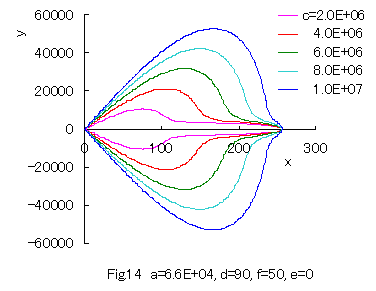 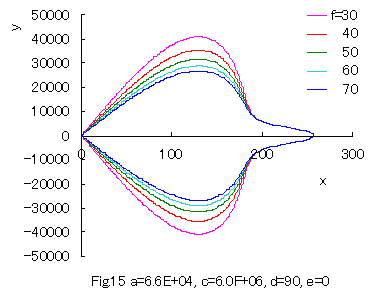 |
|
When the values of some constants are varied, 'spade shaped curves' are obtained as shown in Figs.16 and 17.
|
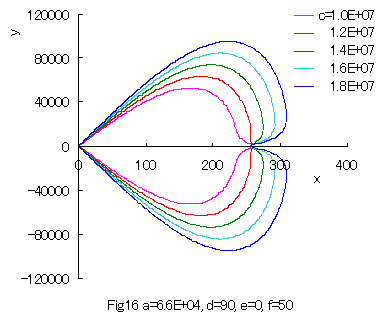 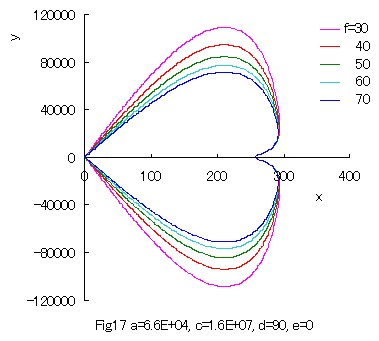 |
|
return
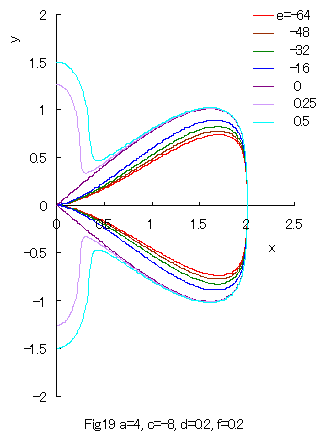
8. The Higher Order Equation II If we replace The solution of the above equation is given as Some examples of the curves which are given by Eq.(34) or its solution Eq.(35) are shown in Figs.18 and 19 in the region of |
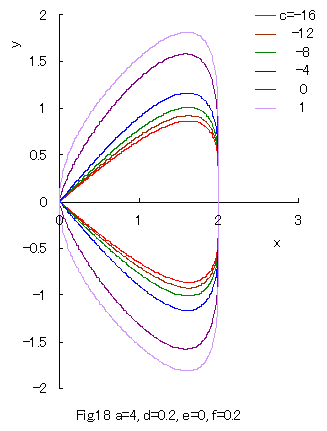
|
|
As seen in Fig.19, a closed curve does not exist within
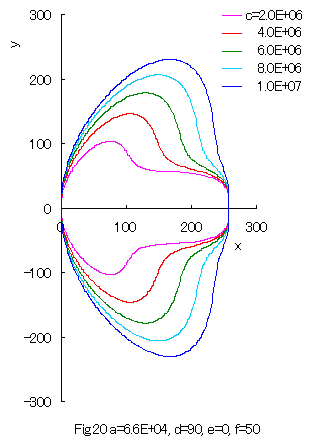
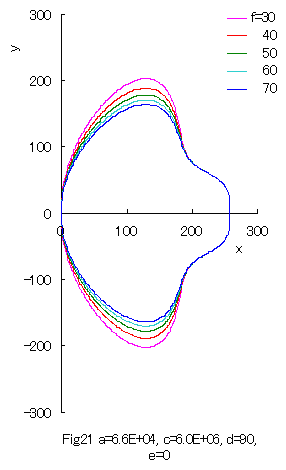
Furthermore, some interesting figures can be drawn as shown in Figs.20 and 21 corresponding to Figs.10 and 11, or to Figs.14 and 15 respectively. |
|
|
return
9. Sites and papers in which this site is cited
|
_ returning to the page which opened just before with 'return' of browser _
or
_ returning to the HOME with the following button _
| HOME |



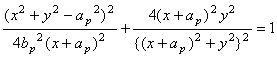 . (7)
. (7)




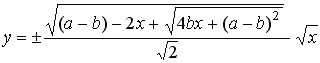 . (9b)
. (9b)
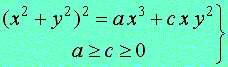 . (10)
. (10)
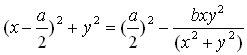 . (11)
. (11)
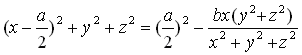 . (13)
. (13)
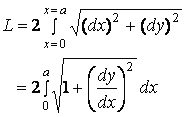 , (14a)
, (14a)
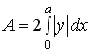 . (14c)
. (14c)
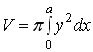 . (15a)
. (15a)
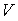 of the egg shaped solid figure with the use of Eq.(15a) or (15b) is given by
of the egg shaped solid figure with the use of Eq.(15a) or (15b) is given by
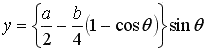 . (18)
. (18)
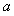 =1, and
=1, and 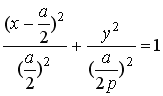 . (21)
. (21)
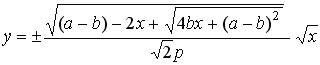 . (20b)
. (20b)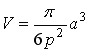 . (22b)
. (22b)
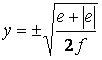 . (28)
. (28)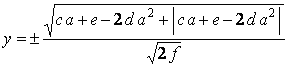 . (30)
. (30)