|
TDCC Laboratory TDCC 研究室 |
| HOME | ENGLISH |
目の形をした曲線群
山本 信雄
クリックすると拡大します。
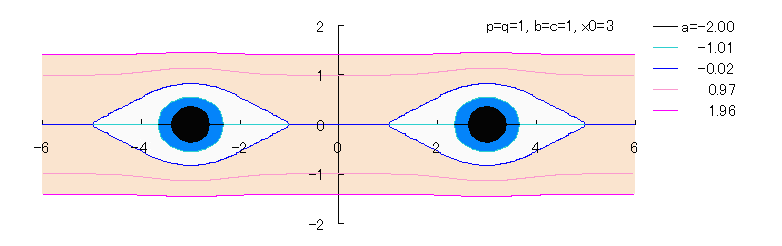
Fig.1b |
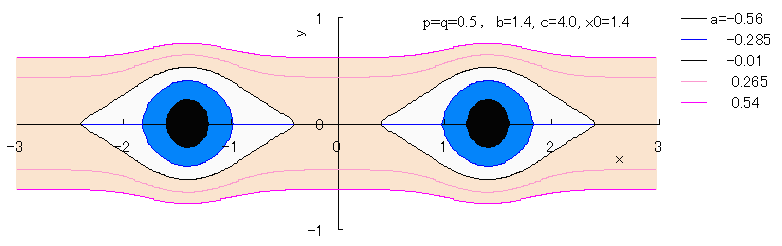
Fig.1c |
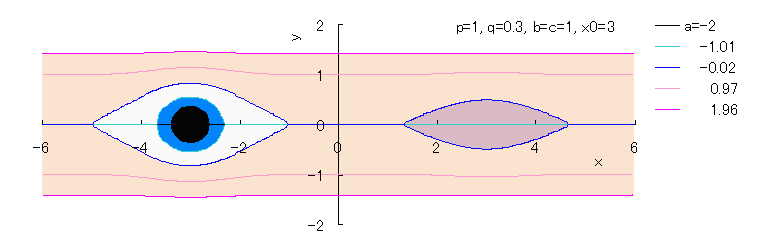
Fig.1d |
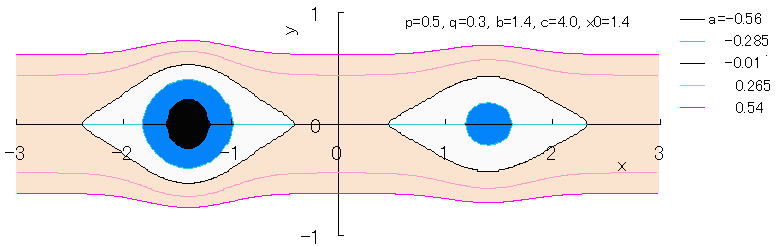
Fig.1e |
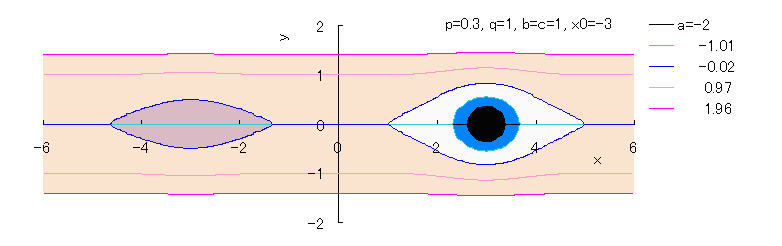
Fig.1f |
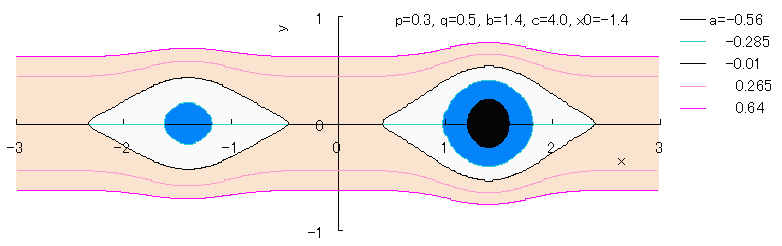
Fig.1g |
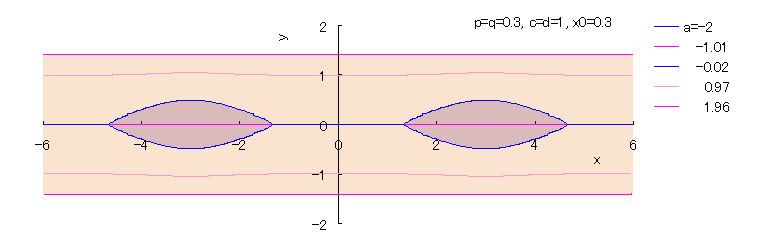
Fig.1h |
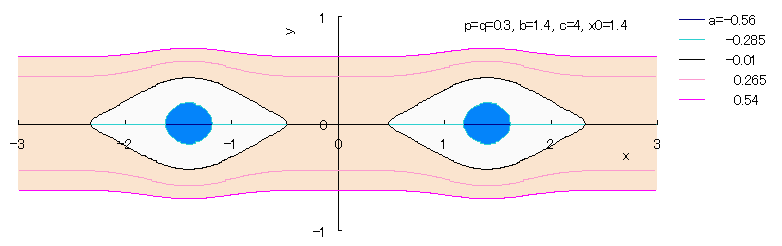
Fig.1i |
|
上図をアニメーションで示しますと次のようです。
なお、画像の自動切り替え方法はこちら
|

|
|---|
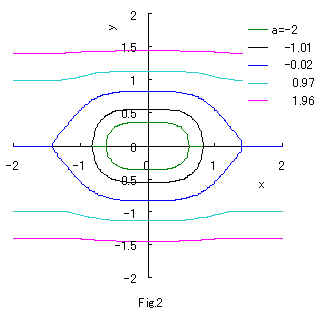
y の 2次指数関数と x の 4次指数関数の混成の次の方程式を考える。
|
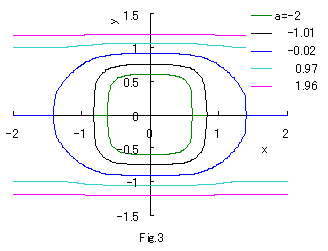
4次指数関数の次の方程式を考える。
|
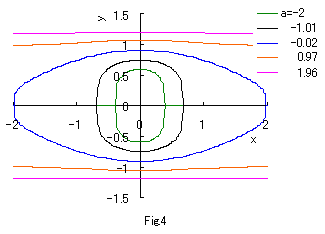
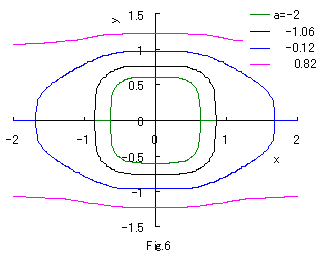
y の 4次指数関数と x の 2次指数関数の混成の次の方程式を考える。
|
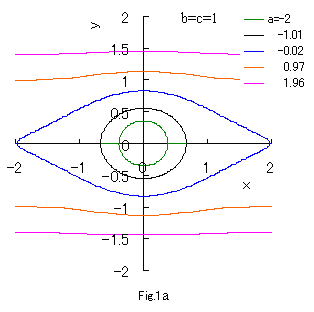
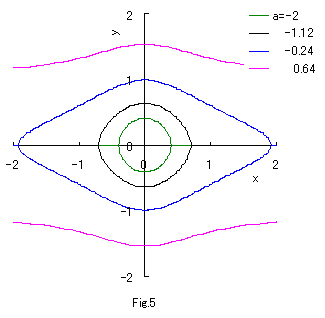
単純な2次式の次の方程式を考える。
|
単純な4次式の場合の次の方程式を考える。
|
1次系双曲線関数の次の方程式を考える。
|
2次系双曲線関数の次の方程式を考える。
|
~ブラウザの「戻る」で 前に開いたページに戻ります~
~または、下のボタンを押して HOME に戻ります~
| HOME |

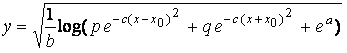 ,
(2b)
,
(2b)
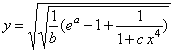 ,
(15)
,
(15)