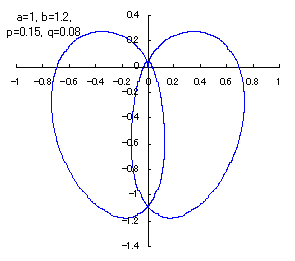TDCC Laboratory
| HOME | JAPANESE |
Equation of Apple Shaped Curve
Nobuo YAMAMOTO
When a Cardioid is deformed into another figure with introducing some exponential functions,
an apple shaped curve is found accidentally.
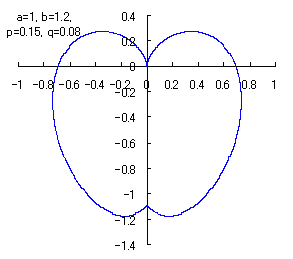 |
 |
|
|
As a reference, when the region of
|
_ returning to the page which opened just before with 'return' of browser _
or
_ returning to the HOME with the following button _
| HOME |
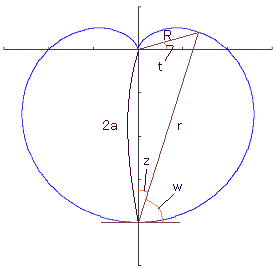

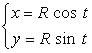 .
(2)
.
(2)
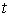 is expanded over the full range, Eq.(3) gives Fig.3.
is expanded over the full range, Eq.(3) gives Fig.3.