TDCC Laboratory
| HOME | JAPANESE |
Equation of Egg Shaped Curve V
Nobuo YAMAMOTO
You can copy and use all the figures in this page freely.
|
This site is introduced in
ПРИЛОЖЕНИЕ НА ТЕХНИКИ ЗА АНАЛИЗ НА ИЗОБРАЖЕНИЯ ПРИ ОЦЕНКА НА ВЪНШНИ ХАРАКТЕРИСТИКИ НА ЯЙЦА ( APPLICATION OF TECHNIQUES FOR IMAGE ANALYSIS IN ASSESSING THE EXTERNAL CHARACTERISTICS OF EGGS) ,
Introduction to Scratch for Programming Beginners-Pen Edition (7) .
|
|
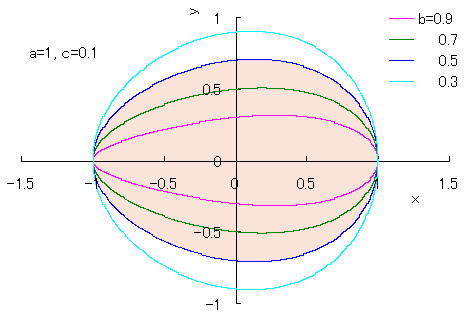
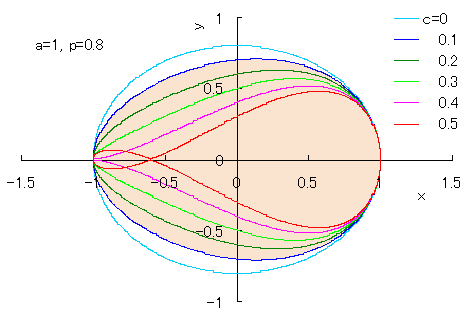
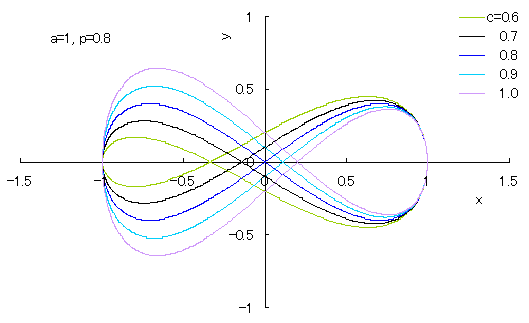
Newly found equation of egg shaped curve is written in the following;
|
|
|
|
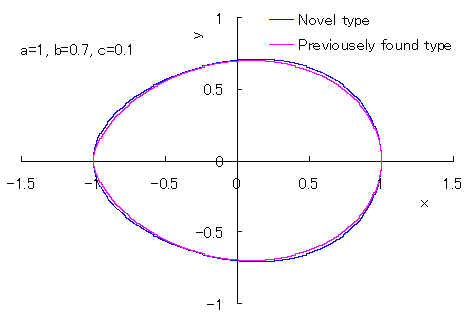
|
|
|
and the previously founded one |
in the case that a=1, b=0.72 and c=0.08 (pink colored curve) and the shape of an actual egg |
|
|
|
|
|
|
In the last, the expression of Eq.(1) in the orthogonal coordinates is led to the follows.
[General expression] |
_ returning to the page which opened just before with 'return' of browser _
or
_ returning to the HOME with the following button _
| HOME |
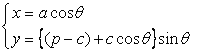 . (2)
. (2)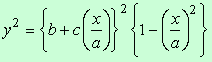 . (3)
. (3)
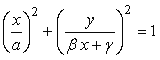 . (4)
. (4) , Eq.(4) leads to the first equation in the page of
, Eq.(4) leads to the first equation in the page of