TDCC Laboratory
TDCC 研究室
| HOME | ENGLISH |
卵形の曲線を表す方程式 VI
山本信雄
本ページの図形は自由にコピーして自由にご使用できます。
|
本サイトは
GENERATING AVIAN EGG USING RATIONAL BEZIER QUADRATIC CURVES
に紹介されています。
|
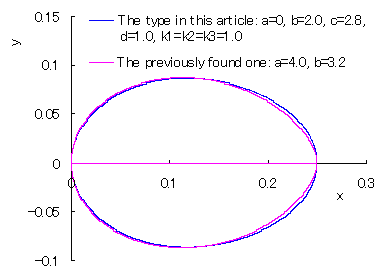
|
|
|
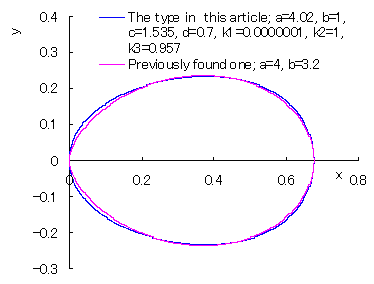
山本が見つけたもの(Previously found one)との比較。 ただし、後者は座標の移動や図形の伸縮を行っている。 |
|
|
|
|
|
|
|
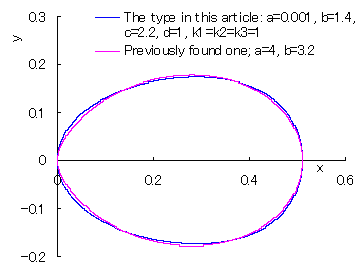
山本が見つけたもの(Previously found one)との比較。 ただし、後者は座標の移動や図形の伸縮を行っている。 |
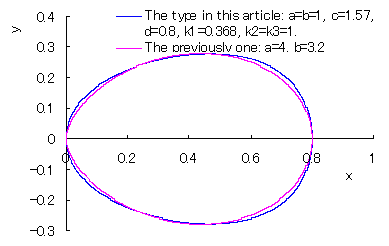
|
|
|
|
1つの例として、a=0, b=1.5, c=2.2, d=k1=k2=k3=1 の場合と現実の卵との比較を図8に示します。ただし、パラメータ値 a, b は、図1のときより少し変えています。図8を見て分かるように、凸形ひずみ円からの変形による卵形曲線の現実の卵の形との一致はあまりよくありません。
|
~ブラウザの「戻る」で 前に開いたページに戻ります~
~または、下のボタンを押して HOME に戻ります~
| HOME |