
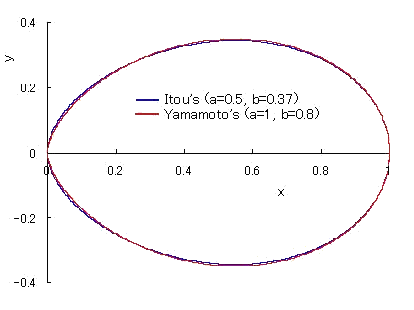
Fig.4 Comparison between the egg shaped curve
of 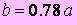 (pink colored curve) (pink colored curve)
and the shape of an actual egg
|
The curve in the case that 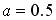 and and 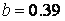 (in general, the case of
(in general, the case of 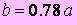 ) gives the closest shape to an actual egg.
The comparison between the curve in this case and the shape of an actual egg is shown in Fig.4. ) gives the closest shape to an actual egg.
The comparison between the curve in this case and the shape of an actual egg is shown in Fig.4.
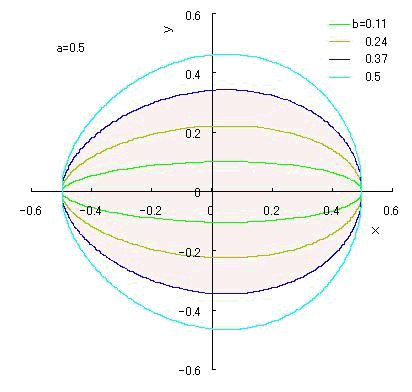
The each curve a, b, c and d shown in Fig.3 is corresponding to the each range of 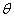 discribed in the following equations;
discribed in the following equations;
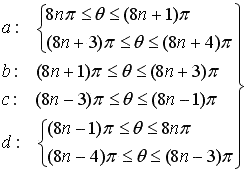 ,
(2) ,
(2)
where n is an integer.
As Eq.(2) is a little complicated to recognize the each range, we will show the typical case of n=0 in Eq.(2) as the followings;
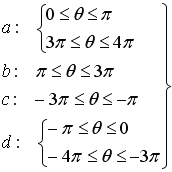 .
(2)' .
(2)'
However, as an area of a, b, c or d as shown in Fig.3 is duplicated as seen in the above equation while each area intersects complicatedly,
so the distinction of the each area is not understood well yet.
Therefore, when only the middle part of the range of 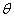 in the above equation is picked out so as not to be duplicated,
we can show a simple description in respect to the range of
in the above equation is picked out so as not to be duplicated,
we can show a simple description in respect to the range of 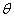 as follows. as follows.
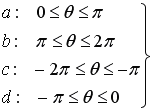 .
(2)'' .
(2)''
[Reference] Relation between 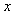 and and 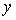 indicating the curves shown in Fig.3 indicating the curves shown in Fig.3
If we take the square of the both sides of the each equation in Eq.(1),
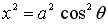 (3)
and
(3)
and
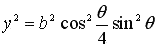 .
(4) .
(4)
If we apply the sinusoidal formula 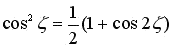 and and
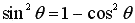 into Eq.(4), into Eq.(4),
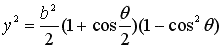 . .
Substituting Eq.(3) into the above equation, we obtain
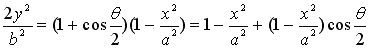 . .
If we arrange the above equation more clearly,
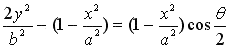 . .
If we take the square of the both sides of the above equation,
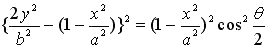 . .
Applying the sinusoidal fomula 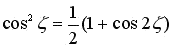 into the above equation, we obtain that
into the above equation, we obtain that
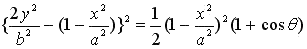 . .
By substituting Eq.(1) in the above equation, Eq.(1) is led to
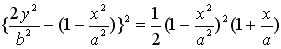 . .
If we arrange the above equation more clearly, we obtain the 5th order equation as the following;
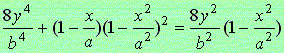 .
(5) .
(5)
The order number of such the obtained equation is more than that of Yamamoto's egg equation
(refered in
 ) by 'a unit'. ) by 'a unit'.
2. Egg shaped curve as a section made by cutting a Pseudo-sphere by means of inclined plane
(Written by Mr. ITOU)
It is well known that a section made by cutting a cone by means of inclined plane does not reveal an egg shaped curve but an ellipse.
On the other hand, a section made by cutting a pseudo-sphere reveals an egg shaped curve as shown in Fig.5.
|

 direction for the comparison.
direction for the comparison.
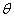 .
.
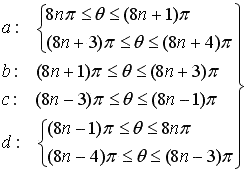 ,
(2)
,
(2)
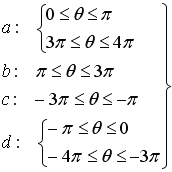 .
(2)'
.
(2)'
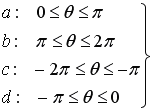 .
(2)''
.
(2)''
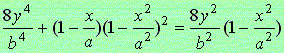 .
(5)
.
(5)