TDCC Laboratory
| HOME | JAPANESE |
Heart Curve II b
Nobuo YAMAMOTO
You can copy and use all the figures in this page freely.
|
1. Preface
2. Fundamental properties
|
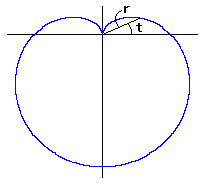 |
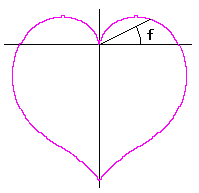 |
|
|
|
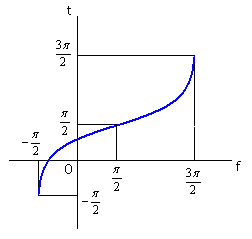 |
|
from |
|
Moreover, in order to obtain beautiful shape of heart figure, both of the coefficient |
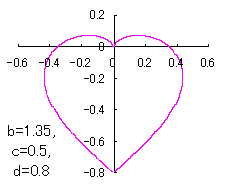 |
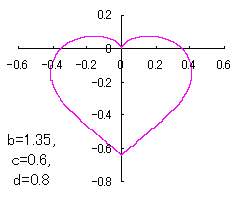 |
|
|
|
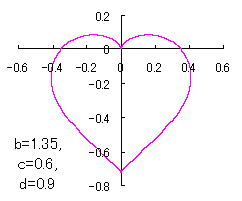 |
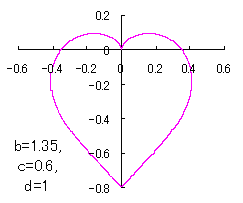 |
|
|
|
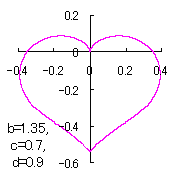 |
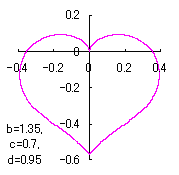 |
|
|
|
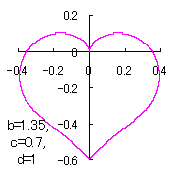 |
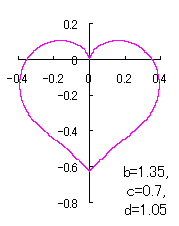 |
|
|
|
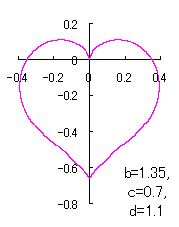 |
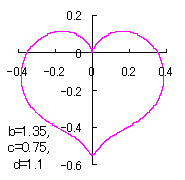 |
|
|
|
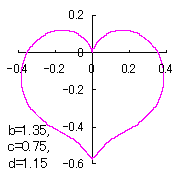 |
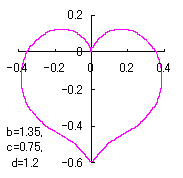 |
|
|
|
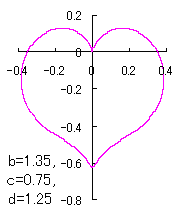 |
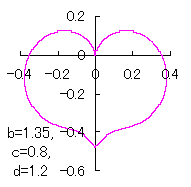 |
|
|
|
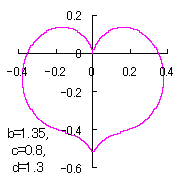 |
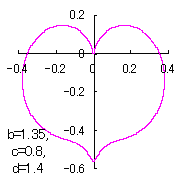 |
|
|
|
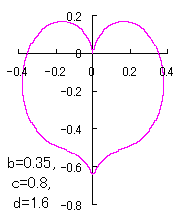 |
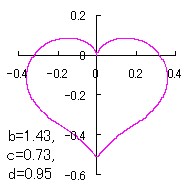 |
|
|
|
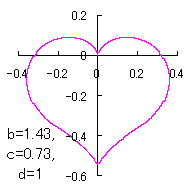 |
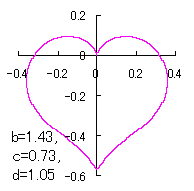 |
|
|
|
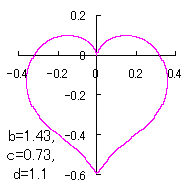 |
 |
|
|
|
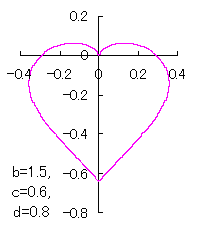 |
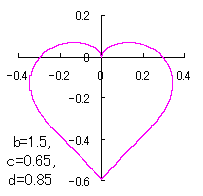 |
|
|
|
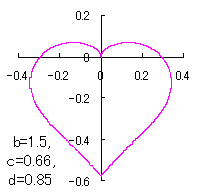 |
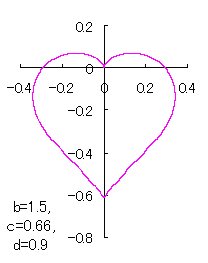 |
|
|
|
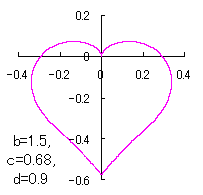 |
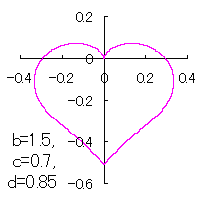 |
|
|
|
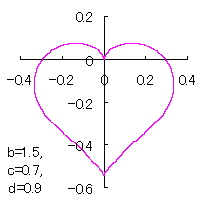 |
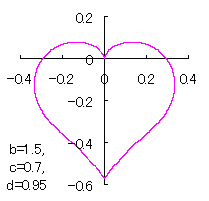 |
|
|
|
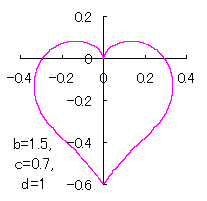 |
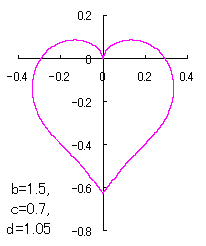 |
|
|
|
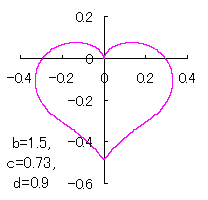 |
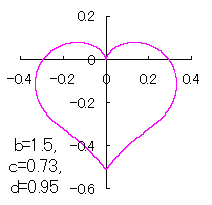 |
|
|
|
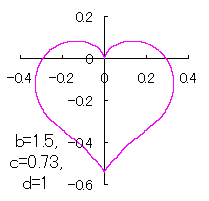 |
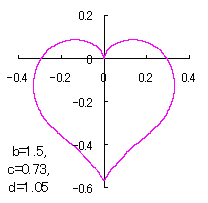 |
|
|
|
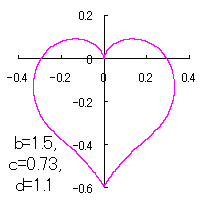 |
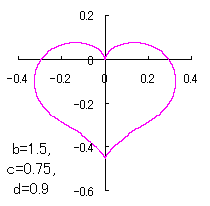 |
|
|
|
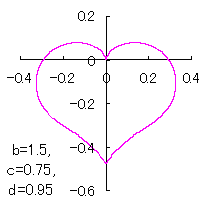 |
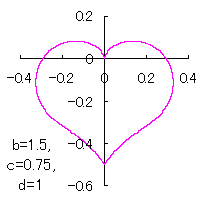 |
|
|
|
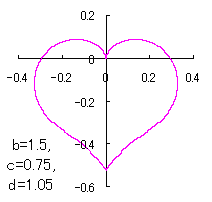 |
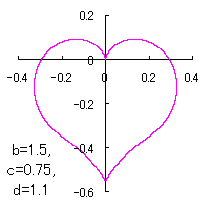 |
|
|
|
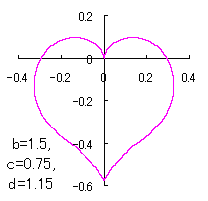 |
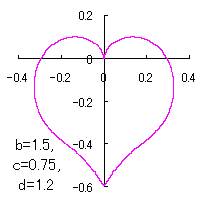 |
|
|
|
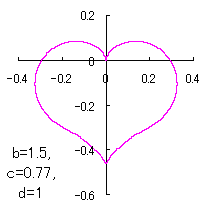 |
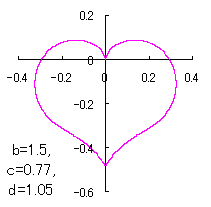 |
|
|
|
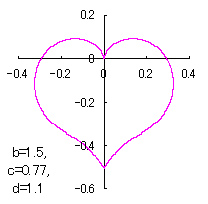 |
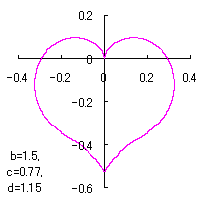 |
|
|
|
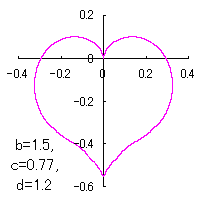 |
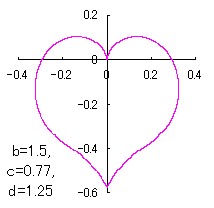 |
|
|
|
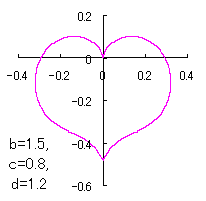 |
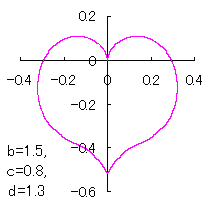 |
|
|
|
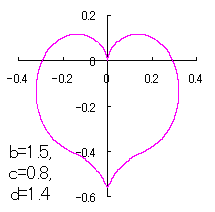 |
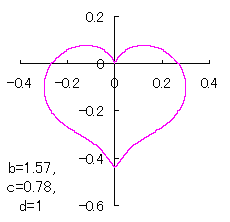 |
|
|
|
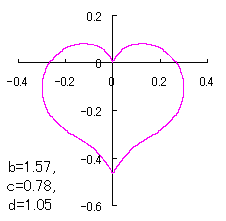 |
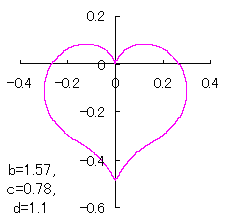 |
|
|
|
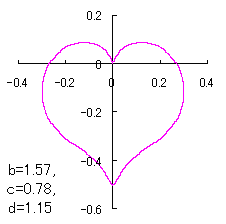 |
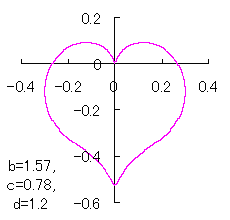 |
|
|
|
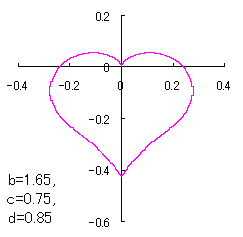 |
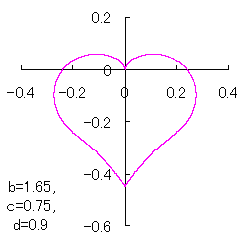 |
|
|
|
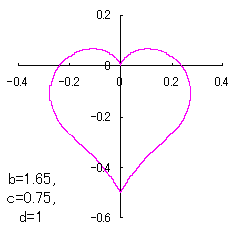 |
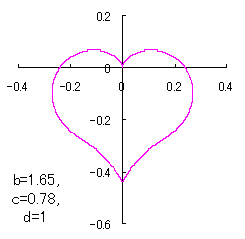 |
|
|
|
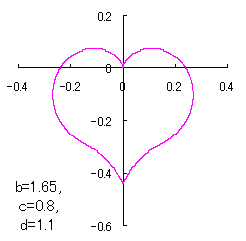 |
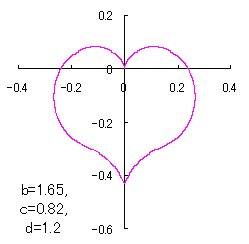 |
|
|
|
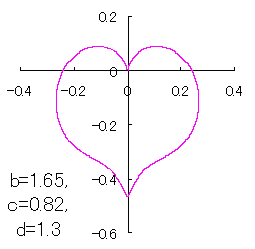 |
|
|
 |
|
|
|
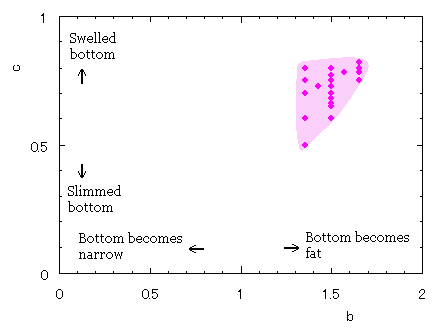
a heart curve may be found Herein, pink colored area represents its region, and dark pink colored dots represents data points which are obtained when heart curves are displayed as above. |
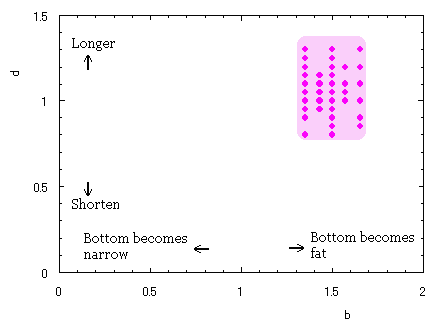 |
|
|
|
a heart curve may be found Herein, pink colored area represents its region, and dark pink colored dots represents data points which are obtained when heart curves are displayed as above. |
The other types of curves besides the heart shaped ones are also obtained as follows. |
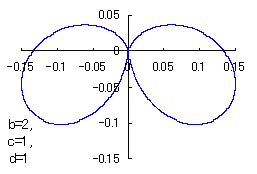 |
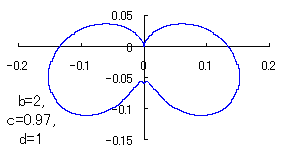 |
|
|
|
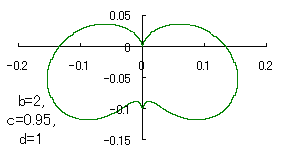 |
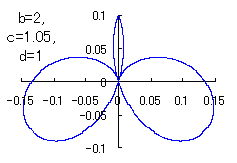 |
|
|
|
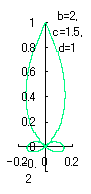 |
|
|
|
When the above figures are painted, these are shown in the followings. 4. The case using the inverse-sinusoidal function with narrower period interval
|
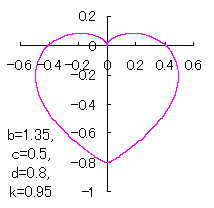 |
 |
|
|
|
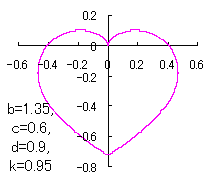 |
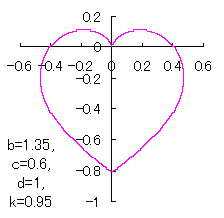 |
|
|
|
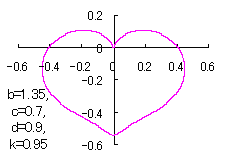 |
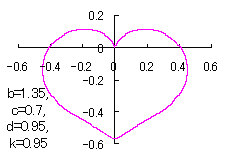 |
|
|
|
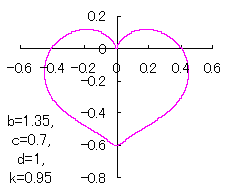 |
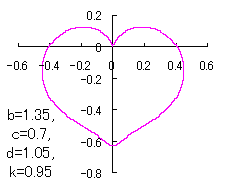 |
|
|
|
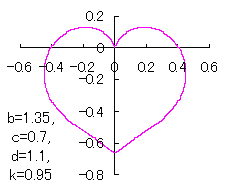 |
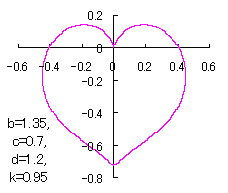 |
|
|
|
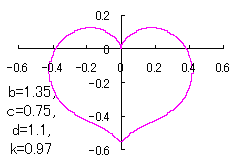 |
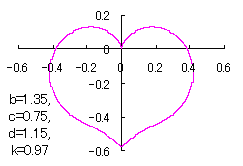 |
|
|
|
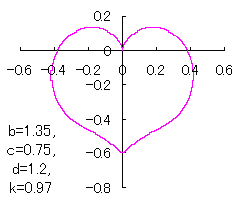 |
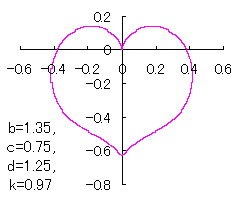 |
|
|
|
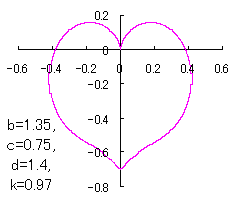 |
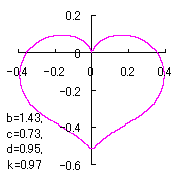 |
|
|
|
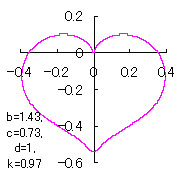 |
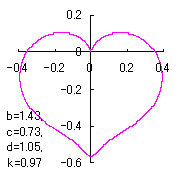 Fig.25b Fig.25b |
|
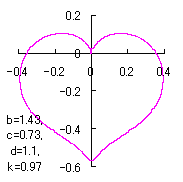 |
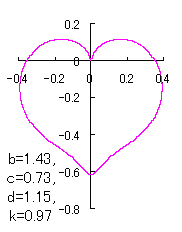 |
|
|
|
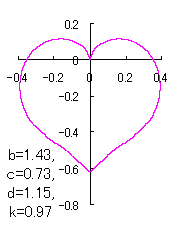 |
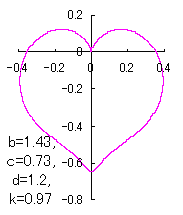 |
|
|
|
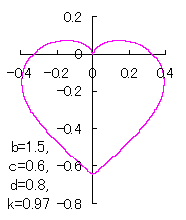 |
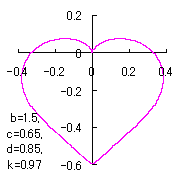 |
|
|
|
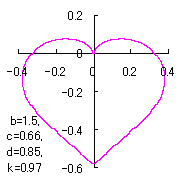 |
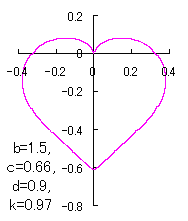 |
|
|
|
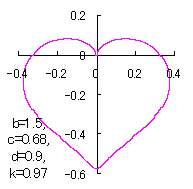 |
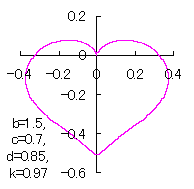 |
|
|
|
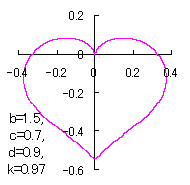 |
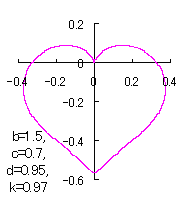 |
|
|
|
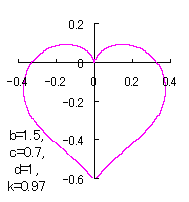 |
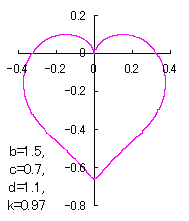 |
|
|
|
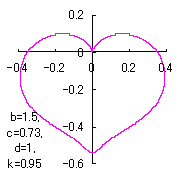 |
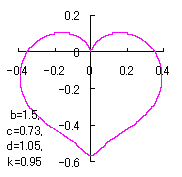 |
|
|
|
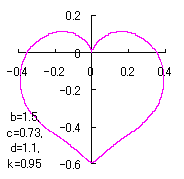 |
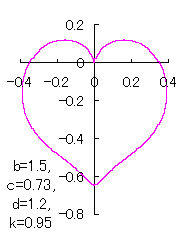 |
|
|
|
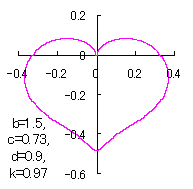 |
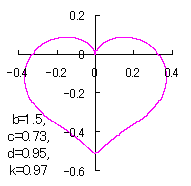 |
|
|
|
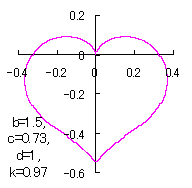 |
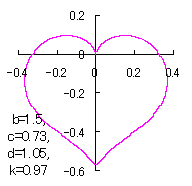 |
|
|
|
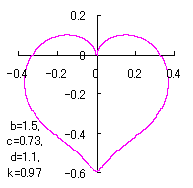 |
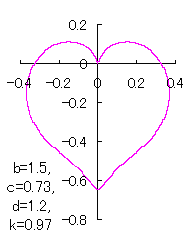 |
|
|
|
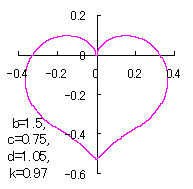 |
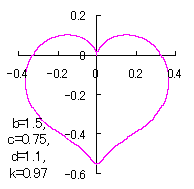 |
|
|
|
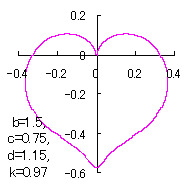 |
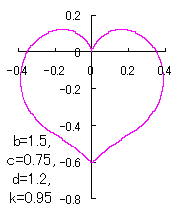 |
|
|
|
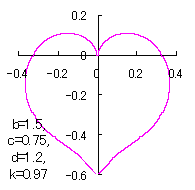 |
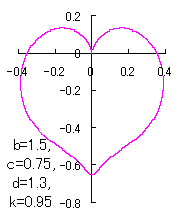 |
|
|
|
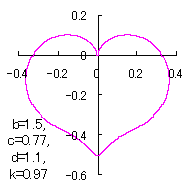 |
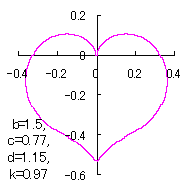 |
|
|
|
 |
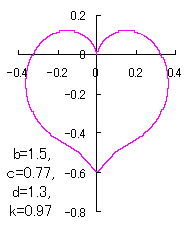 |
|
|
|
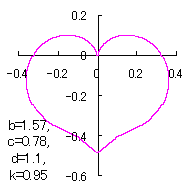 |
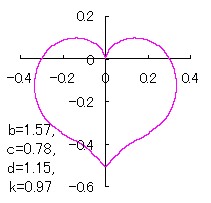 |
|
|
|
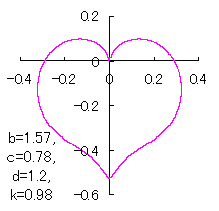 |
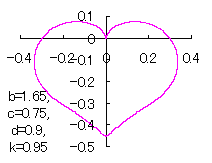 |
|
|
|
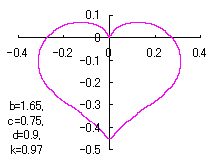 |
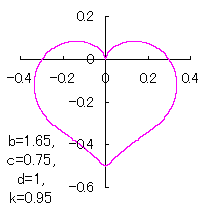 |
|
|
|
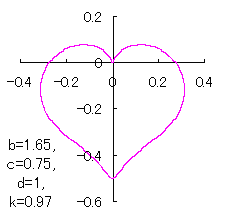 |
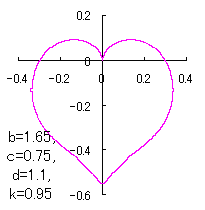 |
|
|
|
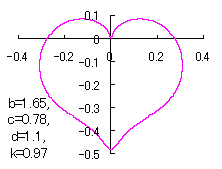 |
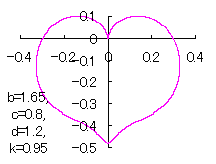 |
|
|
|
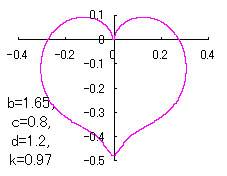 |
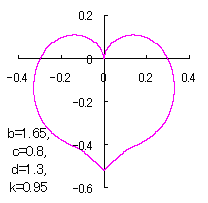 |
|
|
|
|
When the above figures are painted, these are shown in the followings.
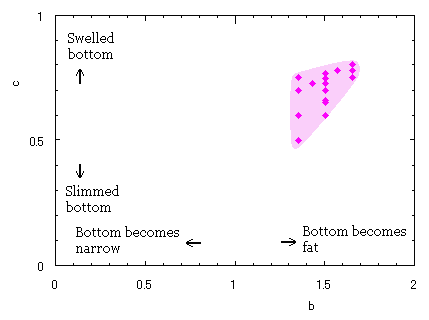
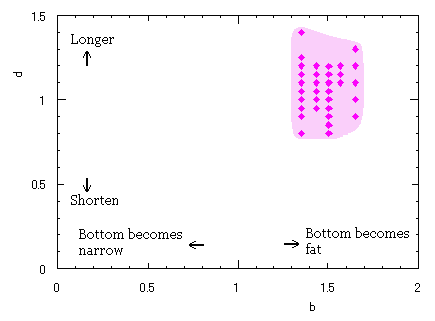
In another method, slightly different shaped heart curves are obtained and shown in |
 |
|
|
|
in which a heart curve may be found Herein, pink colored area represents its region, and dark pink colored dots represents data points which are obtained when heart curves are displayed as above. Herein, nearly fixed in the range of from 0.95 to 0.98. |
 |
|
|
|
in which a heart curve may be found Herein, pink colored area represents its region, and dark pink colored dots represents data points which are obtained when heart curves are displayed as above. Herein, nearly fixed in the range of from 0.95 to 0.98. |
5 The case using the tangential function as
|
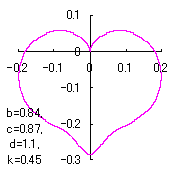 |
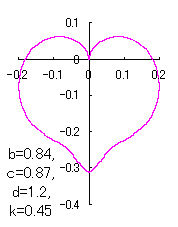 |
|
|
|
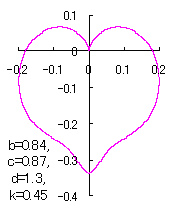 |
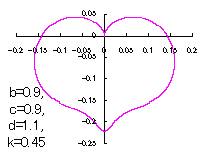 |
|
|
|
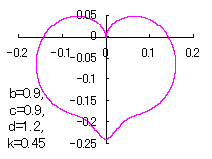 |
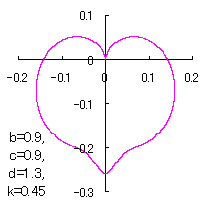 |
|
|
|
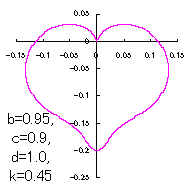 |
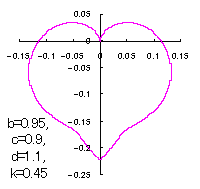 |
|
|
|
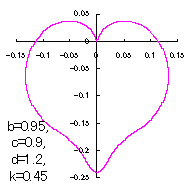 |
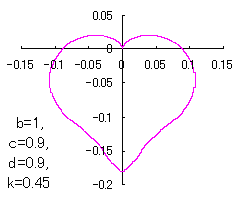 |
|
|
|
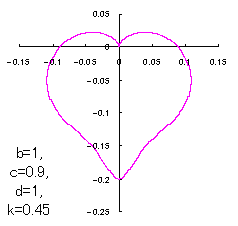 |
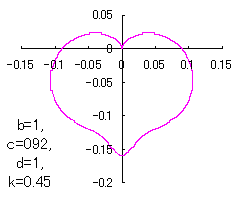 |
|
|
|
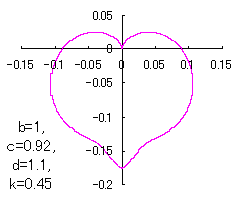 |
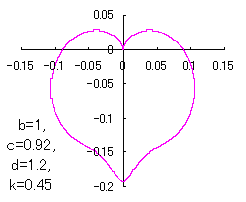 |
|
|
|
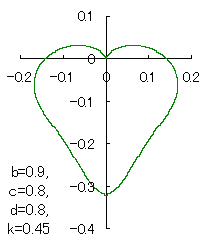 |
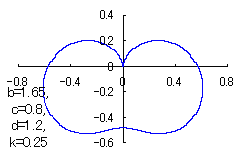 |
|
|
|
|
When the above figures are painted, these are shown in the followings.
6 The case using the inverse hyperbolic-tangential function as
|
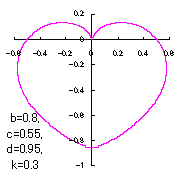 |
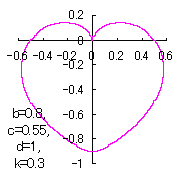 |
|
|
|
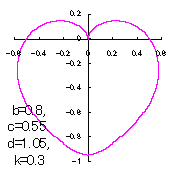 |
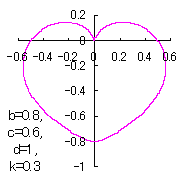 |
|
|
|
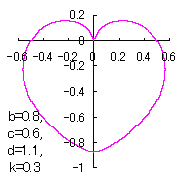 |
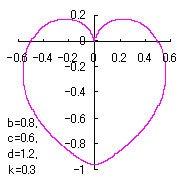 |
|
|
|
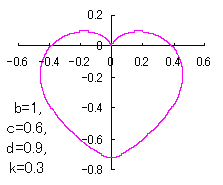 |
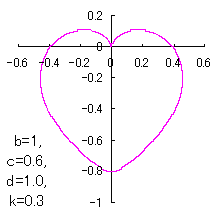 |
|
|
|
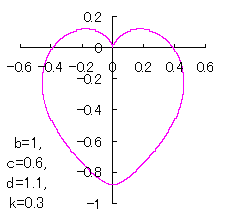 |
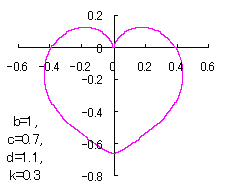 |
|
|
|
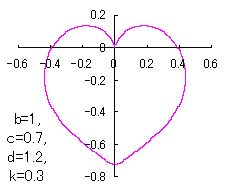 |
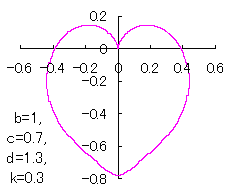 |
|
|
|
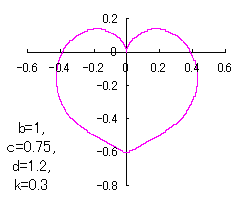 |
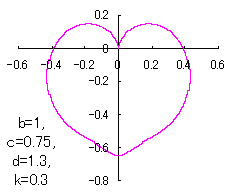 |
|
|
|
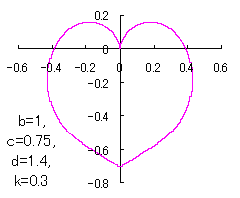 |
|
|
|
When the above figures are painted, these are shown in the followings.
7 The case using the inverse Fermi distibution function as
|
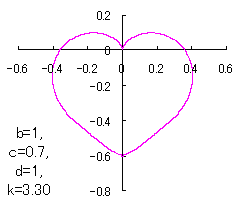 |
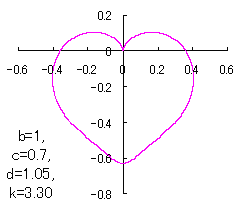 |
|
|
|
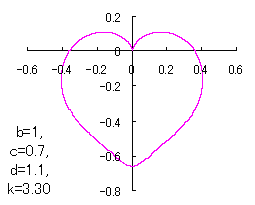 |
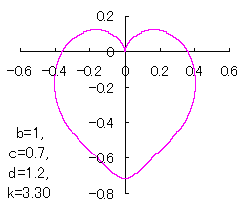 |
|
|
|
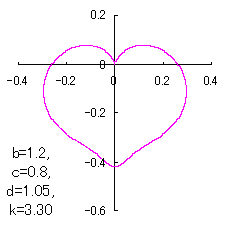 |
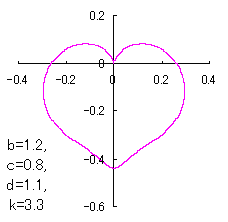 |
|
|
|
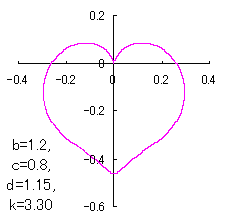
|
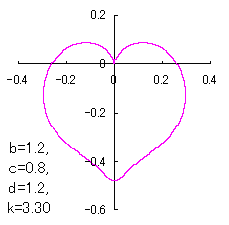
|
|
|
|
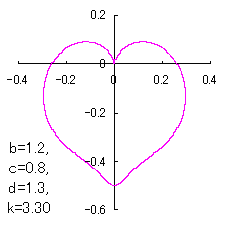
|
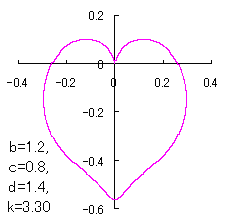
|
|
|
|
|
When the above figures are painted, these are shown in the followings.
|
_ returning to the page which opened just before with 'return' of browser _
or
_ returning to the HOME with the following button _
| HOME |
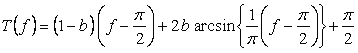 , (4)
, (4)

































































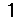





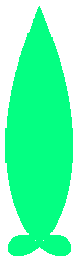
 , (5)
, (5)

































































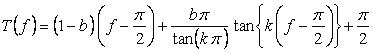 , (6)
, (6)
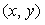 coordinate data of heart curves are obtained. Examples of such obtained curves are shown in Fig.37, where
coordinate data of heart curves are obtained. Examples of such obtained curves are shown in Fig.37, where 















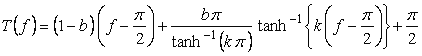 , (7)
, (7)















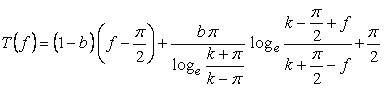 , (9)
, (9)









