TDCC Laboratory
| HOME | JAPANESE |
Heart Curve III
Nobuo YAMAMOTO
You can copy and use all the figures in this page freely.
Equation of heart curve is tried to be composed with the use of the exponential function
in the same way as described in the page of the equation of a curve expressing the shape of a letter S.
|
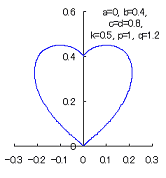
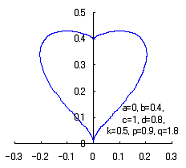
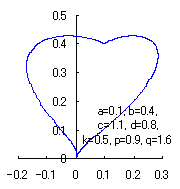
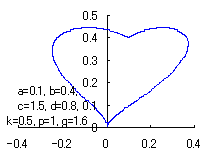
1. Method1
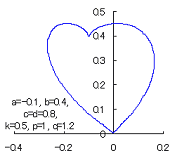
The following two equations are supposed to be able to display a heart curve as the value of the intermediate variable |
|
|
|
|
|
|
|
|
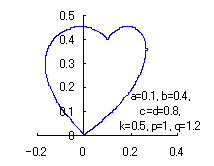
|
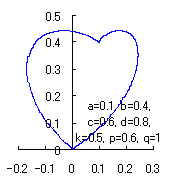
|
|
|
|
|
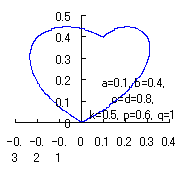
|
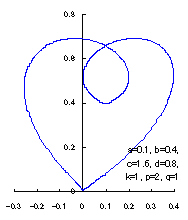
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
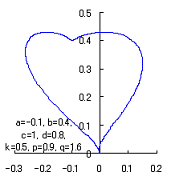
|
|
|
|
|
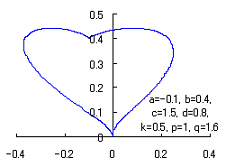
|
|
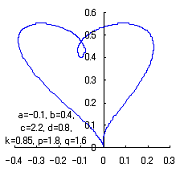
|
|
|
|
|
|
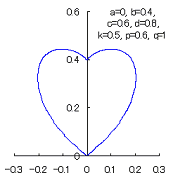
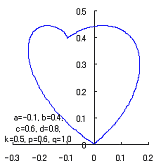
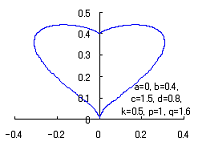
When the above figures are painted, these are shown in the followings.
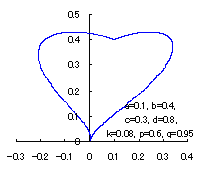
The following two equations are considered corresponding to Eqs.(1) and (2).
|
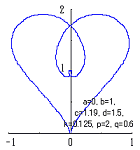
|
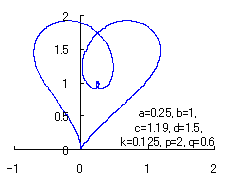
|
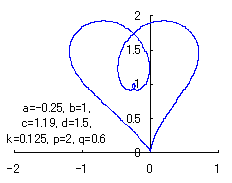
|
|
|
|
|
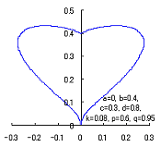
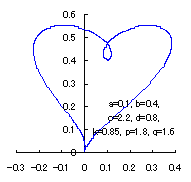
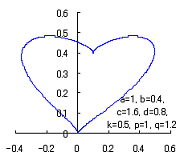
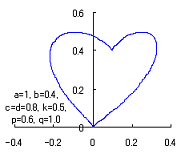
4. Method 4
The following two equations are considered corresponding to Eqs.(1) and (2).
|
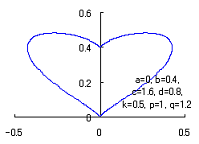
|
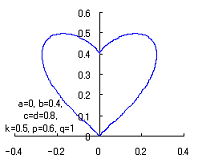
|
|
|
|
|
|
|
|
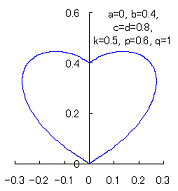
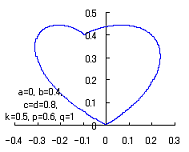
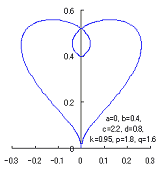
When the above figures are painted, these are shown in the followings.
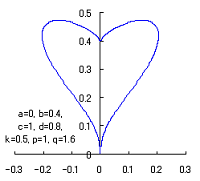
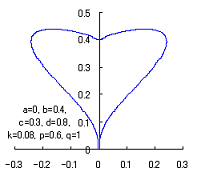
The following two equations are considered corresponding to Eqs.(1) and (2).
|
|
|
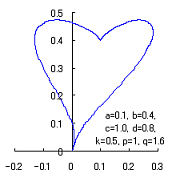
|
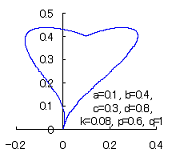
|
|
|
|
|
|
|
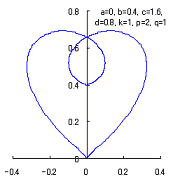
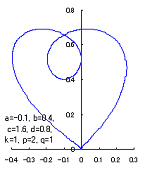
When the above figures are painted, these are shown in the followings.
|
_ returning to the page which opened just before with 'return' of browser _
or
_ returning to the HOME with the following button _
| HOME |
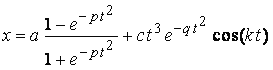 , (1)
, (1)
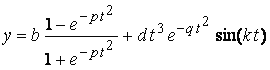 , (2)
, (2)












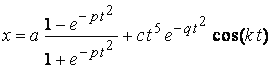 , (3)
, (3)
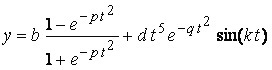 ,
(4)
,
(4)












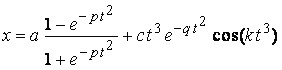 ,
(5)
,
(5)
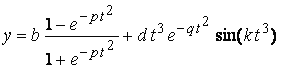 ,
(6)
,
(6)










