TDCC Laboratory
TDCC 研究室
| HOME | ENGLISH |
ミラープローブ法による弱電離磁化プラズマ中の電子温度異方性の測定
山本 信雄
|
1. まえがき
磁化プラズマ中の電子温度異方性または電子速度分布異方性を測定するために、1970年頃に 八田吉典教授 (東北大学名誉教授、故人)のご指導の下に、 ミラープローブ法 ( 同左) を開発しました。この方法は中程度磁場、中程度プラズマ密度、および、低電子温度に適し、この範囲のプラズマでは、電子温度異方性の測定法は多分他にないようです。 2. 本方法の原理
測定原理は次のようである。仮定として、プローブ捕集面 図1において、電子の運動に関する磁気モーメント保存則は、 ここに、 つぎに、エネルギー保存則は、 ここに、 とする。 (1)、(2)式より、 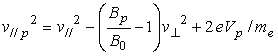 . (4) . (4)
電子がプローブの捕集面Spに突入する条件は、 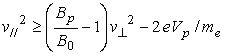 . (5) . (5)
これは、後に 図1の面積 面積 ただし、 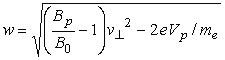 . (8) . (8)
ここで、 に規格化してあり、 (6)式を(7)式に代入し、捕集面 dSp 全域にわたって積分すると、 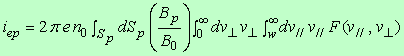 . (10) . (10)
上式がミラープローブに流入する電子電流の基本式である。 プラズマ電子が磁場に平行、垂直の各温度が異なり、そりぞれ、 ここに、 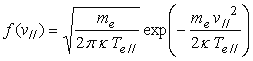 , (12) , (12)
および、 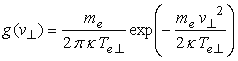 , (13) , (13)
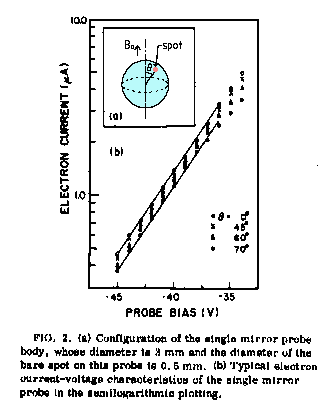
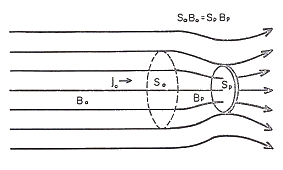
のように表される。 3. 本方法の具体化 本方法を実現する最も簡単な方法が、図2のように、小さな強磁性の球体を磁場中プラズマに適用することである。この球面上のスポット部分だけを電子捕集面として用い、他は電気的にシールドする。ただし、球体のスケールは電子のラーモア半径よりもずっと大きく、かつ、測定対象の磁化プラズマのスケールよりずっと小さくする必要がある。 |
|

|
|
|
図2 ミラープローブ法の原理図と測定例 [下記論文(2)掲載] |
図3 実際のミラープローブ(内球は鋼鉄) [下記論文(4)掲載] |
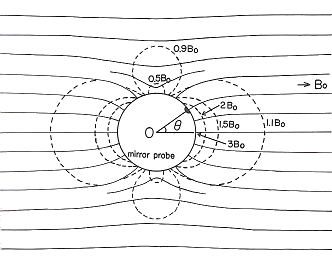
スポット面の法線方向とプラズマ中の均一磁場方向の角度θを0度から70度まで変えることにより、スポット面上の磁場の強さをプラズマ中の均一磁場の3倍から1倍に変えることができる。すなわち、局所的な磁気ミラー比を3から1に変えることができる。この球ミラープローブの周囲の磁場を描いたものが図4である。
4.1.1 TPC装置(名古屋大学 [旧]プラズマ研究所)
名古屋大学 (旧)
プラズマ研究所
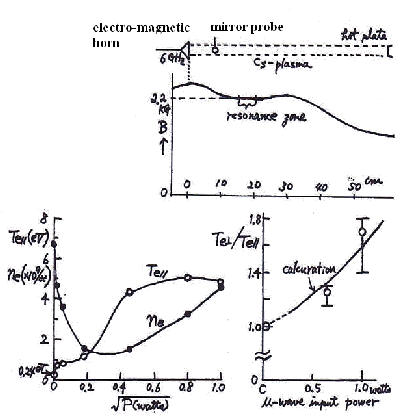
(1989年に核融合科学研究所として岐阜県土岐市に移転)の TPC装置 において本方法による測定を実施した。本装置は、接触電離によって極めて静かな電子温度が0.2eVという低温のほぼ完全電離の定常セシウムプラズマが生成され、中性ガスが存在せず、無衝突のプラズマが実現される。通常は電子温度異方性は観測されなかったが、1ワットの6GHzのマイクロ波で外部磁場に垂直方向に電子サイクロトロン共鳴加熱を施したところ、磁場に垂直方向と平行方向との各電子温度の比の値が最大 |
|
|
図5 セシウムプラズマにおける電子サイクロトロン加熱による 電子温度異方性の出現 |
|
しかし、その後の追試では、その再現性は確認できず、等方性を示した。その理由は、実験時間が進行するにつれ、セシウム原子がマイクロ波窓に付着して、マイクロ波がプラズマ中に放射できなくなったためと考えられる。もう少し、粘り強く装置を整備し直して、追試実験を行えば再現できたかもしれない、と後悔している。
|
|
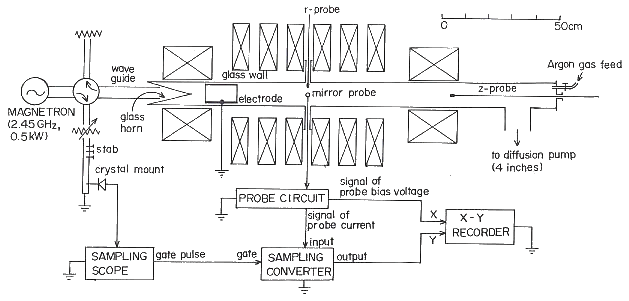
| 図6 TPM装置 |
|
|
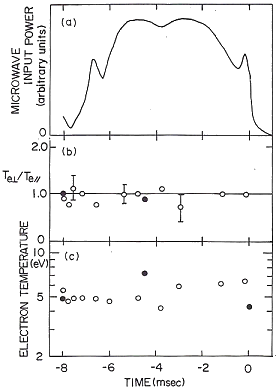
図7 定常プラズマの電子温度異方性
実験条件は、中性ガス圧(アルゴン) p=0.20 mTorrで、 閉じ込め用の外部ミラー磁場のミラー比が 白丸は |
|
4.1.4 TEPSON 装置(東北大学工学部電子工学科 [旧]八田研究室)
図8は 東北大学 工学部電子工学科(旧)八田研究室の TEPSON 装置 を示す。前装置と同様に2.45GHzマイクロ波による電子サイクロトロン共鳴加熱(ECRH)によって、アルゴンガスの定常プラズマを生成し、外部ミラー磁場に閉じ込めている。
|
|
|
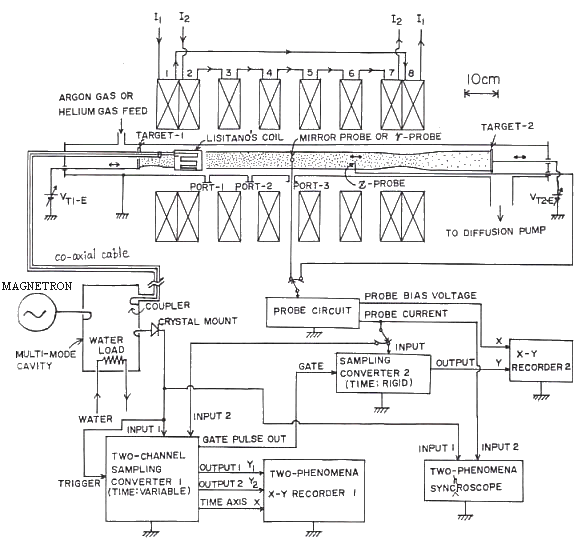
図8 TEPSON 装置
|
|
|
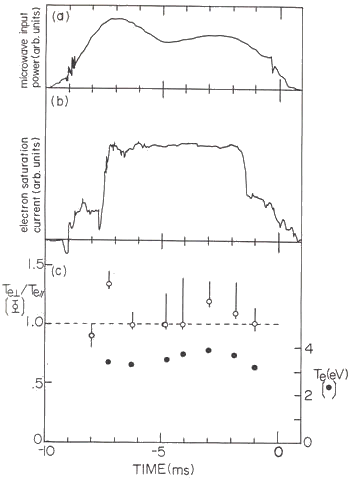
図9 定常プラズマの電子温度異方性
実験条件は、中性ガス圧(アルゴン) p=0.45 mTorrで、 均一磁場(ミラー比 |
|
4.2 非定常プラズマ
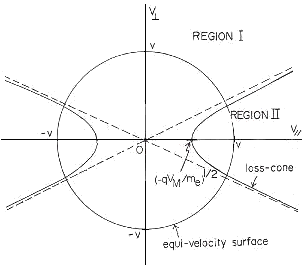
しかし、非定常プラズマ、すなわち、過渡プラズマ、その代表例として、閉じ込め用ミラー磁場中のアフターグローの電子は外部ミラー磁場によって閉じ込められるロスコーン分布をしていると考えられる。このロスコーン分布の平均エネルギーは、磁場に垂直方向が平行方向よりも大きいと考えられるので、ミラープローブによって、観測できないかと考えて、実験を遂行した。その結果、電子速度分布異方性が、以下に記述するように、観測された。
|
|
|
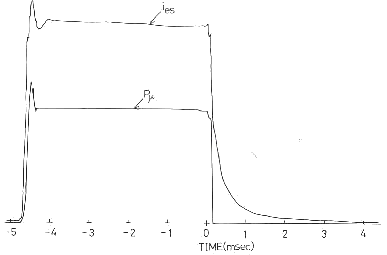
図10 マイクロ波入力パルスとプローブの飽和電子電流
|
|
|
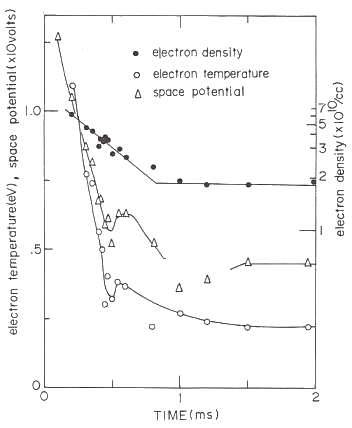
図11 アフターグローにおけるプラズマ諸量の時間推移
実験条件は、中性ガス圧(アルゴン) p=0.25 mTorrで、 閉じ込め用の外部ミラー磁場のミラー比が |
|
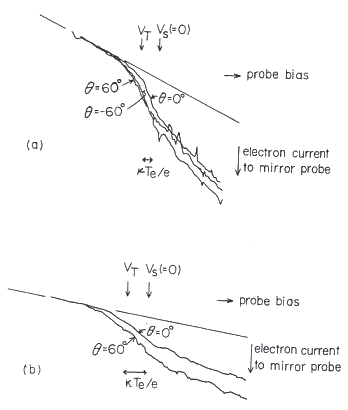
図12は、ミラープローブ特性の実測の2例を示している。全体が傾斜しているのは、プローブ電圧を調節する可変抵抗に、何らかの漏れ定電流が流れていたためであるが、この定電流は線形的に加算されているだけなので、プローブ特性には全く影響がない。
|
|
|
図12 ミラープローブ特性の実測の2例
実験条件は、閉じ込め用の外部ミラー磁場の ミラー比が (a)図はミラー磁場のミラー点における 空間電位が電子温度の電圧換算の2倍程度、 中性ガス圧(アルゴン) p=0.12 mTorr、 アフターグロー開始からの時刻 t=1.6 msec, (b)図はミラー磁場のミラー点における 空間電位が電子温度の電圧換算と同程度、 中性ガス圧(アルゴン) p=0.20 mTorr、 アフターグロー開始からの時刻 t=0.8 msec, |
|
|
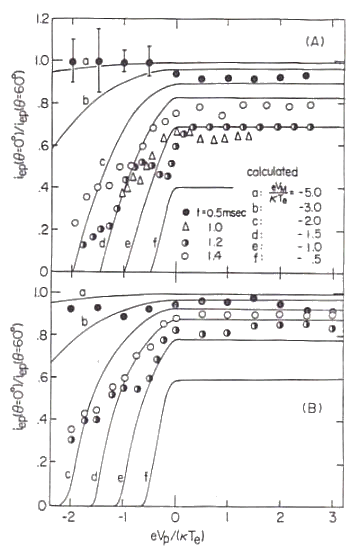
図13 各時刻ごとにまとめた複数個のプローブ特性データ 実曲線は(24)式のロスコーン分布から予測される理論特性。 実験条件は、中性ガス圧(アルゴン) p=0.20 mTorrで、 閉じ込め用の外部ミラー磁場のミラー比が (a)図は |
|
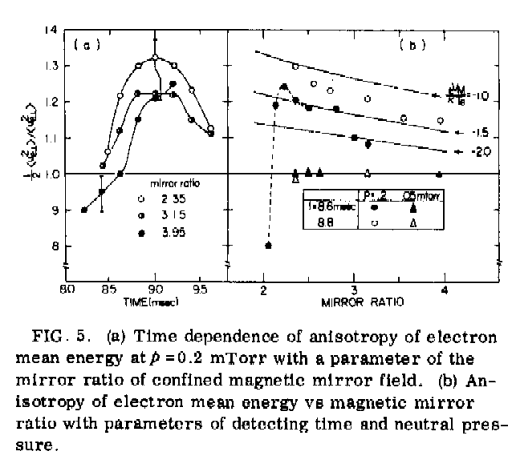
図15(a)は、図13で推定されたロスコーン分布をもとに計算された電子の平均運動エネルギー異方性 |
|
| 図14 ロスコーン分布を規定する速度位相空間 |
|
| 図15 ミラー磁場中アフターグローの電子速度分布異方性の出現 |
|
4.2.2 TEPSON 装置(東北大学工学部電子工学科 [旧]八田研究室)
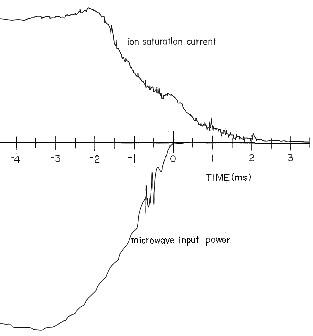
前節4.1.4項のTEPSON装置で、図16のような間歇的な方形波マイクロ波パルスで定常プラズマを発生させた後、パルスを切った直後にアフターグローが残ることが図中から分かる。このアフターグローにおけるプラズマ諸量の時間推移を、参考として、図17に示す。 |
|
|
|
図16 マイクロ波入力パルスとプローブの飽和電子電流
|
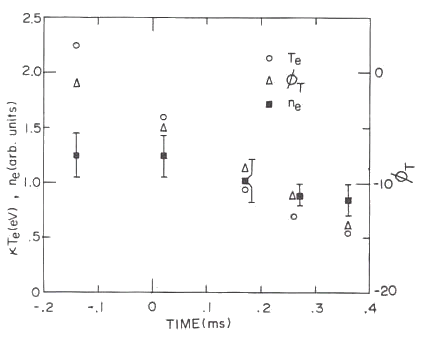
図17 アフターグローにおけるプラズマ諸量の時間推移
白丸は電子温度、白三角は中心プラズマから見たプラズマ左右両端の ターゲット(図21(b)参照)の電位、黒四角はプラズマ密度。 実験条件は、中性ガス圧(アルゴン) p=0.53 mTorrで、 閉じ込め用の外部ミラー磁場のミラー比が |
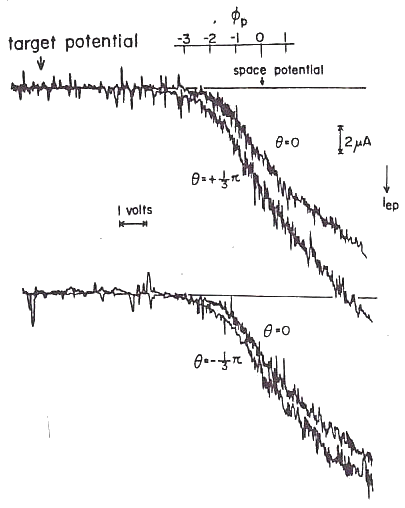
| 図18および19は、ミラープローブ特性の実測の例を数多く示している。 |
|
|
図18 ミラープローブ特性の実測の例
実験条件は、閉じ込め用の外部ミラー磁場のミラー比が 中性ガス圧(アルゴン) p=0.53 mTorr、 アフターグロー開始からの時刻 t=0.17 msec. |
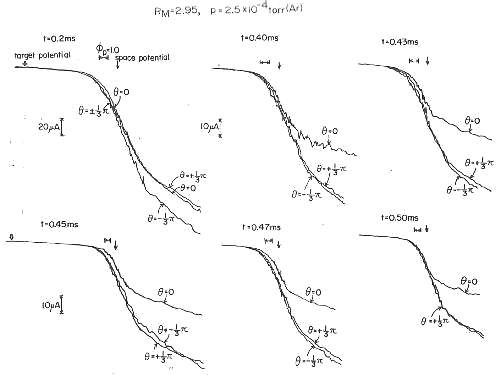
|
|
図19 同左 実験条件は、閉じ込め用の外部ミラー磁場のミラー比が 中性ガス圧(アルゴン) p=0.25 mTorr、 アフターグロー開始からの時刻 t は図中に記載。 |
|
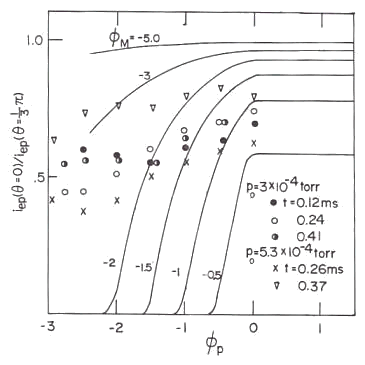
得られた複数個のプローブ特性を、各時刻ごとに図13のようにまとめて示すと、図20にようになる。縦軸は、ミラープローブの捕集面の角度を0度と60度の2つの場合で測定した電子電流の比を表し、横軸の |
|
|
|
図20 図13のようにまとめたミラープローブ測定データ
実曲線は(24)式のロスコーン分布から予測される理論特性で、 測定データと合っていない。 |
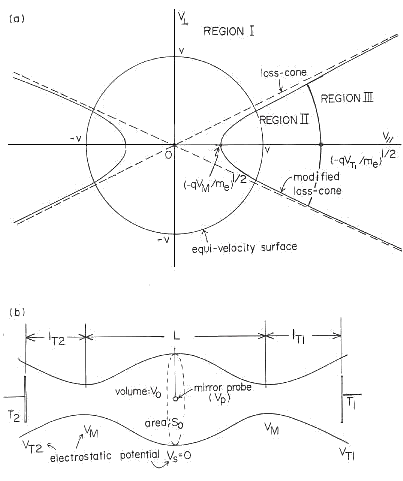
図21 修正されたロスコーン分布を導き出すためのレイアウト
|
|
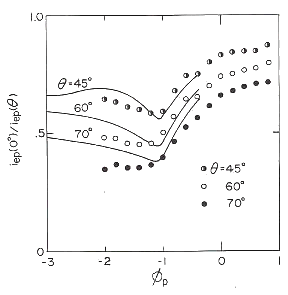
図22に、ミラープローブの捕集面スポット角度毎の測定データを実曲線で表される「修正されたロスコーン分布」から予測される理論的測定カーブとを比較したものである。ここに、横軸は、電子温度で規格化したプローブバイアス |
|
|
|
図22 ミラープローブの捕集面スポット角度毎 の測定データ 実曲線は修正されたロスコーン分布から予測 される理論特性で、測定データとよく合っている。 測定条件は、閉じ込め用の外部ミラー磁場のミラー比が アフターグロー開始からの時刻は t=0.2 msec. |
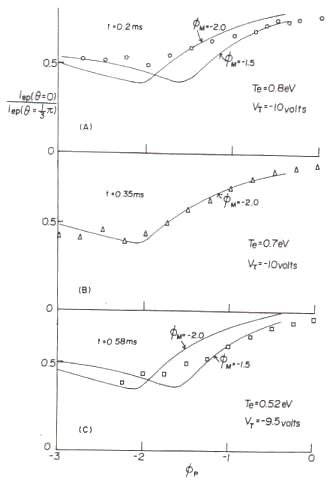
図23 プローブ特性データ
実曲線は修正されたロスコーン分布から予測される 理論特性 測定条件は、閉じ込め用の外部ミラー磁場のミラー比が アフターグロー開始からの時刻は t は図中に記載。 |
|
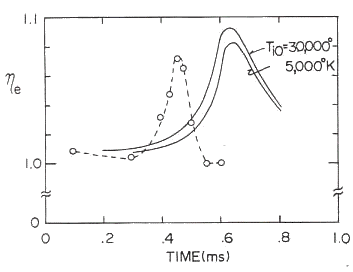
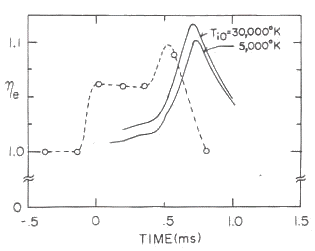
図24から26は、修正されたロスコーン分布を基に計算された電子の平均運動エネルギー異方性 |
|
|
|
図24 異方性の時間推移。実線は理論。
実験条件は、中性ガス圧(アルゴン) p=0.25 mTorr、 閉じ込め用の外部ミラー磁場のミラー比 |
図25 異方性の時間推移(その2)
実験条件は、中性ガス圧(アルゴン) p=0.30 mTorr、 閉じ込め用の外部ミラー磁場のミラー比 |
|
|
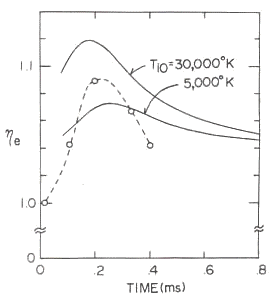
図26 異方性の時間推移(その3)
実験条件は、中性ガス圧(アルゴン) p=0.46 mTorr、 閉じ込め用の外部ミラー磁場のミラー比 |
|
以上のTEPSON 装置での測定結果を 日本物理学会講演会 、 博士論文 、 日本物理学会講演会(その2) に報告してある。
|
|
|
|
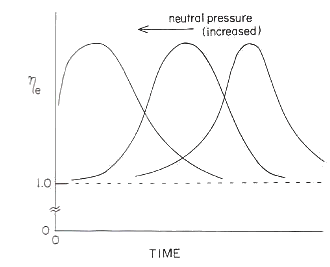
図27 異方性の時間的推移の 中性ガス圧依存性 |
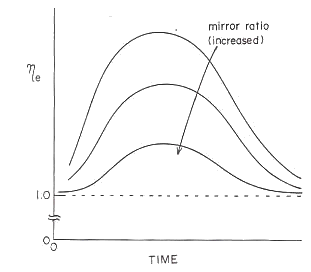
図28 異方性の閉じ込め用外部ミラー磁場の ミラー比に対する依存性 |

|
[coffee break]
(1) お世話になった近藤験 殿
|
|
(2) 日本物理学会・プラズマ核融合分科会および核融合懇談会(現在のプラズマ核融合学会)プラズマ若手グループによるプラズマ夏の学校
|
|
(クリックすると拡大でご覧なれます)
|
||||||
|
|
その後、プラズマ夏の学校は、1967年に長野県麻績郡大岡村(現在は長野市)の聖高原、1968年に長野県上田市菅平、1969年に長野県南佐久郡小海町松原湖、1970年に長野県茅野市白樺湖で行われました。いずれも有名な避暑地でわくわくしたものです。現在もプラズマ核融合学会の若手研究者で継続されています。
|
|
(クリックすると拡大でご覧なれます)
|
||||
|
|
(4) ミラープローブ発表当時の思い出
初めて日本物理学会でミラープローブを発表したとき、当時の名古屋大学プラズマ研究所の 高山一男所長(故人) ( 同左 )から直々に質問と激励のお言葉があり、日本物理学会・プラズマ核融合分科会で一寸話題になりました。 |
~ブラウザの「戻る」で 前頁 に戻ります~
~または、下のボタンを押して HOME に戻ります~
| HOME |
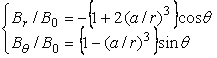 . (14)
. (14)
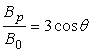 . (17)
. (17)
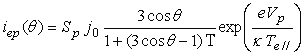 . (21)
. (21)
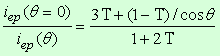 , (22)
, (22)
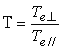 . (23)
. (23)
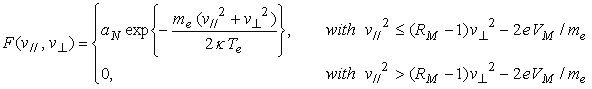 , (24)
, (24)
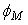 は、閉じ込め用外部磁気ミラー中心のプラズマ空間電位を基準にしたミラーポイントでのプラズマ空間電位を電子温度で規格化したものである。図23の結果により、修正されたロスコーン分布の妥当性が認められる、と同時に、ミラープローブの測定に信頼性があると判断されよう。
は、閉じ込め用外部磁気ミラー中心のプラズマ空間電位を基準にしたミラーポイントでのプラズマ空間電位を電子温度で規格化したものである。図23の結果により、修正されたロスコーン分布の妥当性が認められる、と同時に、ミラープローブの測定に信頼性があると判断されよう。