TDCC Laboratory
| HOME | JAPANESE |
Measurement of Anisotropy of Electron Temperature in Magnetized Plasma by Magnetic Mirror Probe Method
Nobuo YAMAMOTO
|
1. Introduction
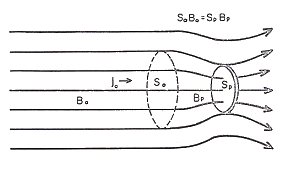
Magnetic mirror probe method ( the same to the left ) has been developed as the diagnostic tool for the measurement of anisotropy of electron temperature or anisotropy of distribution function of electron velocity in magnetized plasma by N. Yamamoto under Prof. Y. Hatta in Tohoku University since 1967. This method can be applied in the middle range of externally applied magnetic field strength, in the middle range of plasma density and in the range of low electron temperature. Another method may not exist in such ranges even in the recent time. 2. Principle of the magnetic mirror probe method
We assume that the scale of the collecting surface of the probe is much larger than the electron cyclotron radius (the Larmoir radius), and is much smaller than the scale of the magnetized plasma. In Fig.1, the conservation law of magnetic momentum of electron is described as where The conservation law of energy of election is described as where From Eqs.(1) and (2), we obtain  . (4) . (4)
As the condition that an electron enters into the collecting surface Sp is 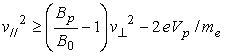 . (5) . (5)
The above equation gives the lower limit of integral when an integration is performed in regard to If we take by the conservation law of magnetic flux. If we take where 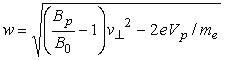 . (8) . (8)
In the above equation, where Substituting Eq.(6) into Eq.(7) and integrating by dSp over all the area Sp, we obtain 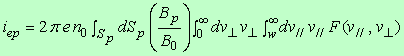 . (10) . (10)
The above obtained equation is the base equation giving the electron current entered into the mirror probe. When the distribution function of electron velocity is followed by bi-Maxwellian which has the parallel and the perpendicular electron temperatures where 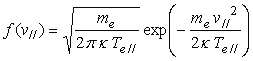 , (12) , (12)
and 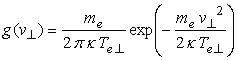 . (13) . (13)
3. Embodiment of this method As to realize the embodiment of this method, the most simple way is to apply a small ferromagnetic sphere to a probe body in the magnetized plasma. Only a spot on the sphere is used the collecting surface of electrons, and the other part is shielded electrically, It is needed that the scale of the spot is smaller than the Lamoir radius, and that the radius of this sphere is smaller than the scale of the magnetized plasma. |
|

|
|
|
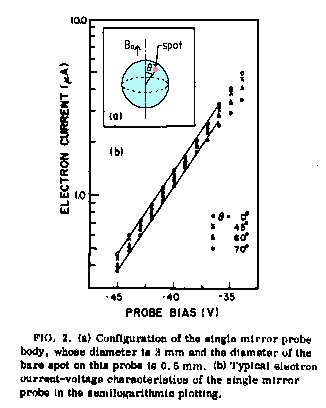
Fig.2 An illustration of the magnetic mirror probe and an example of its measured data [reference (2)] |
Fig.3 The actual magnetic mirror probe made of steel sphere [reference (4)] |
Magnetic field strength on the spot can be varied from the equality to three times of the externally applied magnetic field strength as 4. Measurement examples of anisotropy of electron temperature or anisotropy of distribution function of electron velocity by the magnetic mirror probe method 4.1 Stationary plasma
The measurements of anisotropy of electron temperature have been performed in four species of devices with the use of the mirror probe as below. Although a little data show anisotropy of electron temperature,Most data indicate |
 |
|
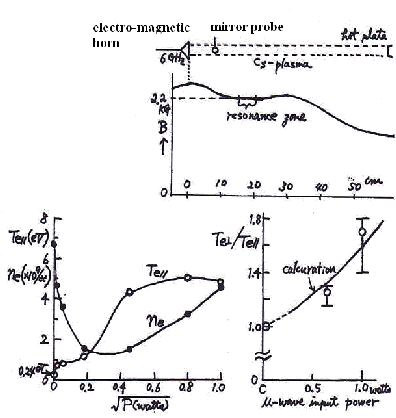
Fig.5 Appearance of anisotropy of the electron temperature by electron cyclotron resonance heating (ECRH) in Cesium plasma |
|
However, follow-up experiments tell that the anisotropy of electron temperature is not found for the reason that the microwave power do not become able to penetrate in to the plasma space as experiment goes on and as Cecium atoms are pasted up to a microwave window. |
|
| Fig.6 TPM device |
|
|
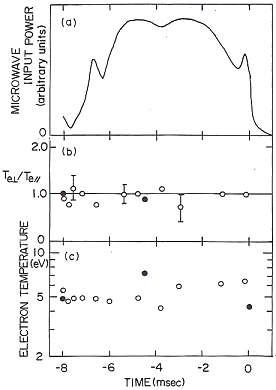
Fig.7 Anisotropy of electron temperature
in stationary plasma Experimental condition is that the neutral gas pressure (Argon gas) is p=0.20 mTorr and the mirror ratios of the externally applied magnetic mirror field are by the white and black circles respectively. |
|
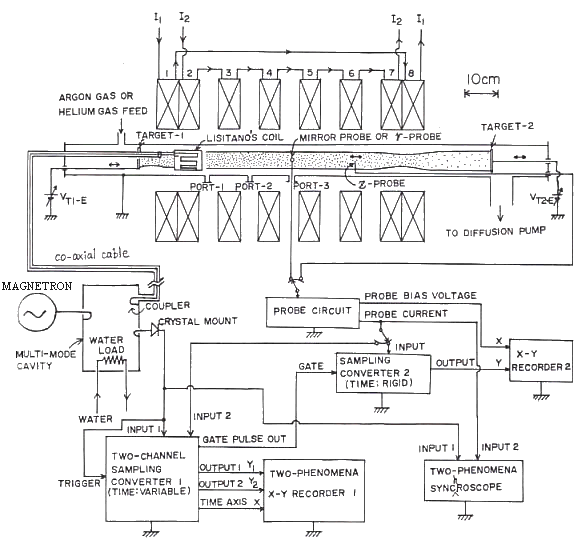
4.1.4 TEPSON device (Hatta Lab., Department of Electronic Engineering, Faculty of Engineering, Tohoku University )
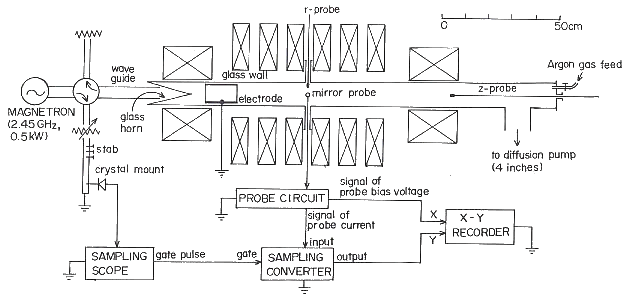
TEPSON device is illustrated in Fig.8. The stationary argon-gas plasma is generated by means of electron cyclotron resonance heating (ECRH) with 2.45GHz microwave power and is confined in the externally applied magnetic mirror field as like as in the TPM machine.
|
|
| Fig.8 TEPSON device |
|
|
Fig.9 Anisotropy of electron temperature in stationary plasma
Experimental condition is that the neutral gas pressure (Argon gas) is p=0.45 mTorr and the mirror ratio of the externally applied magnetic mirror field is (a uniform field of 875 Gauss). |
|
4.2 Unstationary plasma
However, in after-glow plasma confined in a magnetic mirror field, as a typical unstationary i.e. transient plasma, an anisotropy of distribution function of electron velocity has been observed, and the loss-corn distribution function of electron has been confirmed by the mirror probe method as mentioned below.
|
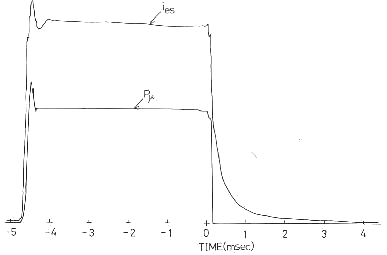 |
| Fig.10 Microwave input pulse and electron saturation current of the probe |
 |
|
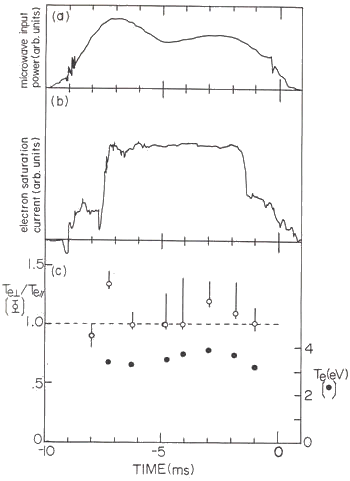
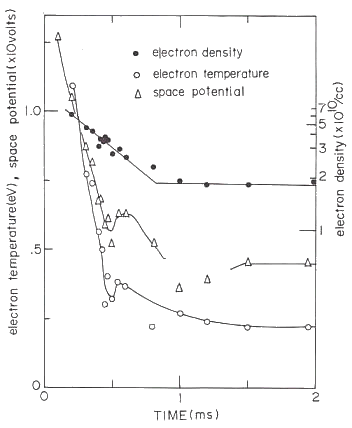
Fig.11 The time transience of several plasma parameters
Experimental condition is that the neutral gas pressure (Argon gas) is p=0.25 mTorr and the mirror ratio of the externally applied magnetic mirror field is |
|
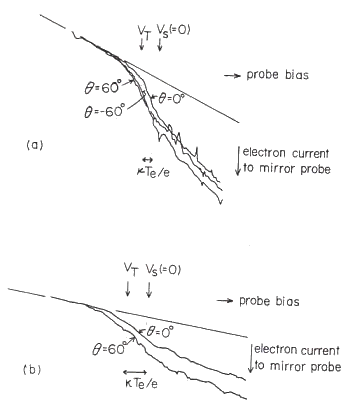
In Fig.12, two examples of the real data measured by the mirror probe are displayed. It is because some constant leak current flows in the varying resister, which is used for adjusting the probe bias, that both data are inclined over all. Nevertheless, this leak current has no influence to a probe characteristics itself as this constant leak current is merely additional to the probe current linearly.
|
|
|
|
Fig.12 Two examples of the real data measured
by the mirror probe Experimental condition is that the mirror ratio of the externally applied magnetic mirror field is and in (a) and (b), the respective space potentials at the mirror point are about two times of and the same with the conversed value of the electron temperature, the respective neutral gas pressures (Argon gas) are p=0.12 and 0.20 mTorr and the respective times after the afterglows start are t=1.6 and 0.8 msec. |
Fig.13 The several plotted data of the probe characteristics
Experimental condition is that the neutral gas pressure (Argon gas) is p=0.20 mTorr, and in (a) and (b), the respective mirror ratios of the externally applied magnetic mirror field are |
|
The time transience of anisotropy of electron mean kinetic energy |
|
|
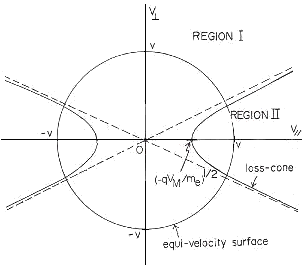
Fig.14 The partition of area in regard to the loss-corn
distribution in the velocity space |
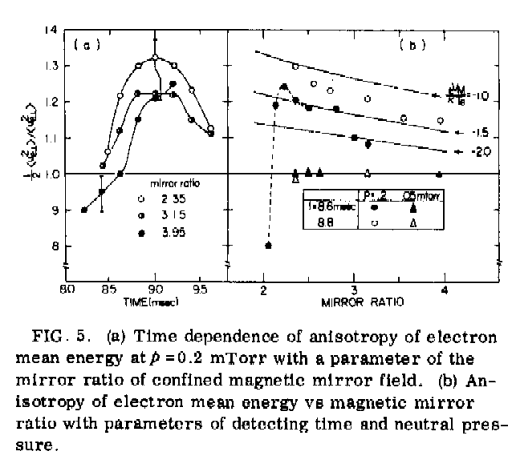
|
|
Fig.15 Appearance of anisotropy in distribution function of electron velocity
of after-glow plasma confined in magnetic mirror field [reference (1)] |
|
4.2.2 TEPSON device (Hatta Lab., Department of Electronic Engineering, Faculty of Engineering, Tohoku University)
After the stationary plasma is generated in TEPSON device, which is taken up in subsection 4.1.4, by pulsed microwave power, the after-glow plasma remains as confirmed as seen in the electron saturation current of the mirror probe as seen in Fig.16.
|
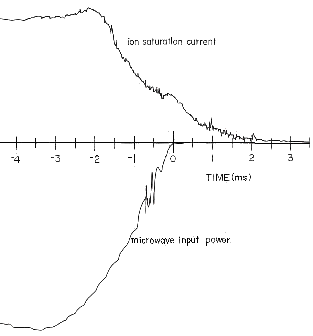
|
|
|
Fig.16 Microwave input pulse and ion saturation current of
the probe |
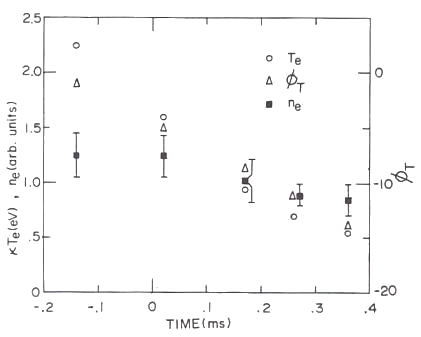
Fig.17 The time transience of several plasma parameters
Circles, triangles and squares indicate electron temperature, floating potential and plasma density respectively. Experimental condition is that the neutral gas pressure (Argon gas) is p=0.53 mTorr and the mirror ratio of the externally applied magnetic mirror field are |
|
Several examples of the real data measured by the mirror probe are displayed in Figs.18 and 19. |
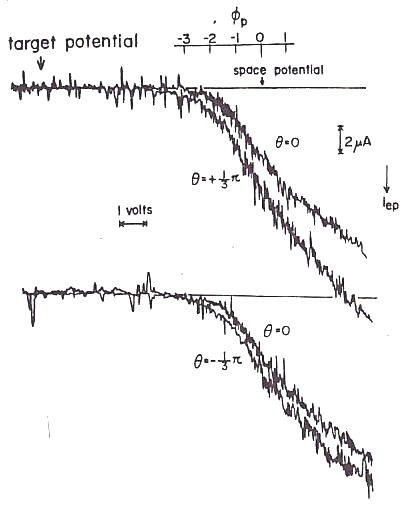
|
|
Fig.18 A pair of the typical real data measured
by the mirror probe Experimental condition is that the mirror ratio of the externally applied magnetic mirror field is the neutral gas pressure (Argon gas) is p=0.53 and the time after the afterglow starts is t=0.17 msec. |
|
|
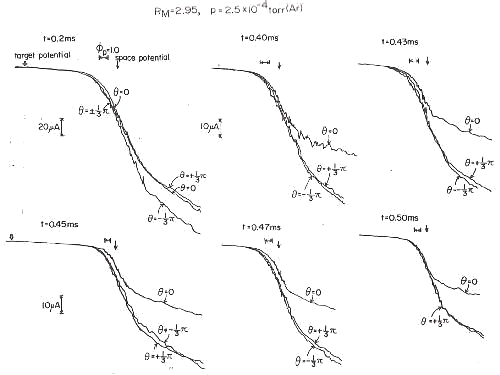
Fig.19 Several examples of the real data measured
by the mirror probe Experimental condition is that the mirror ratio of the externally applied magnetic mirror field is the neutral gas pressure (Argon gas) is p=0.25 mTorr and the time after the afterglow starts is described in the figure. |
|
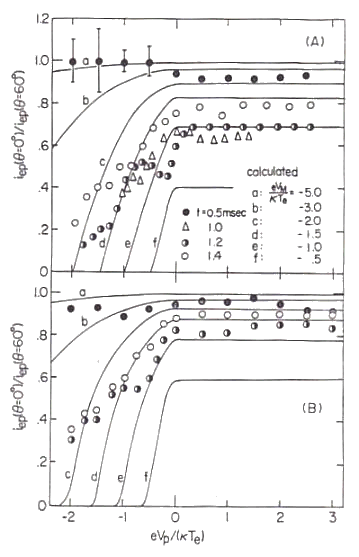
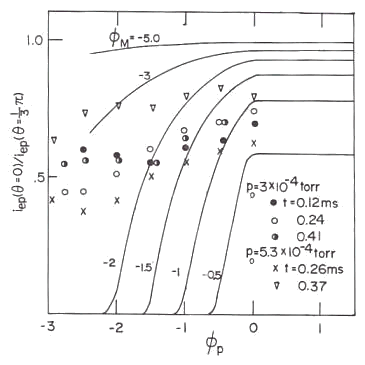
The obtained data of the probe current are plotted in Fig.20 as like as in Fig.13. The vertical axis indicate the ratio of the probe electron current at 60 degree of the spot angle to that at 0 degree, and the horizontal axis indicate the normalized probe bias voltage. The solid curves display the theoretically predicted probe characteristics calculated on the base of a loss-corn distribution function of electrons which is given by Eq.(24).
|
|
|
Fig.20 The several plotted data of the probe characteristics
The solid curves indicate characteristics calculated with the use of Eq.(24). The theoretical curves do not explain the plotted data. 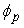 is the probe bias normalized by electron temperature and is the probe bias normalized by electron temperature and
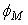 is the space potential normalized by electron temperature is the space potential normalized by electron temperature
at the mirror point of the externally applied magnetic mirror field. |
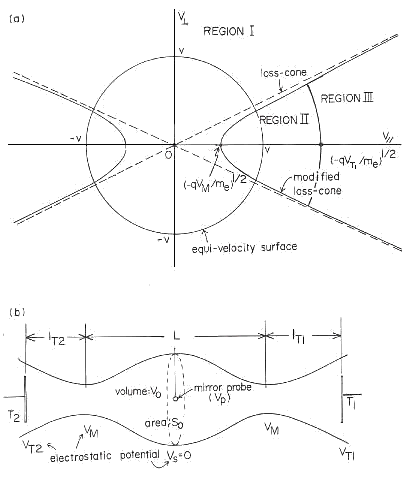
|
| Fig.21 Layouts for deriving "improved loss-corn distribution function" |
|
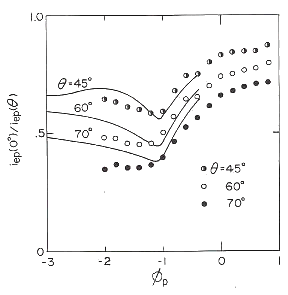
The plotted data measured by the mirror probe with each correcting spot angle are compared with the solid curves which are calculated by "improved loss-corn distribution function of electron velocity" in Fig.22 where the horizontal axis represents the probe bias |
|
|
|
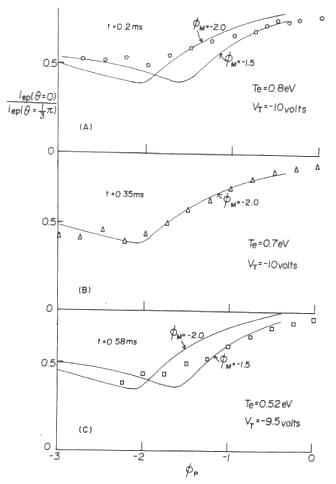
Fig.22 The measured data of the mirror probe
every spot angle temperature. Solid curves are the predicted characteristics obtained from the improved loss-corn distribution function. These curves well explain the measured data. Experimental condition is that the mirror ratio of the externally applied magnetic mirror field is the neutral gas pressure (Argon gas) is p=0.30 and the time after the afterglow starts is t=0.20 msec. |
Fig.23 Probe characteristics data
Solid curves are the same as in Fig.21 where by the electron temperature at the mirror point. Experimental condition is that the mirror ratio of the externally applied magnetic mirror field is the neutral gas pressure (Argon gas) is p=0.30 and the time after the afterglow starts is described in the figure. |
|
The time transience of anisotropy of electron mean kinetic energy |
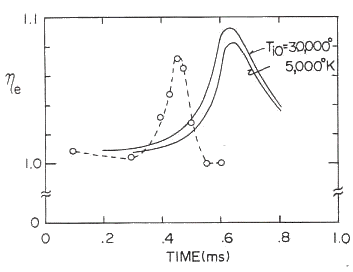
|
|
|
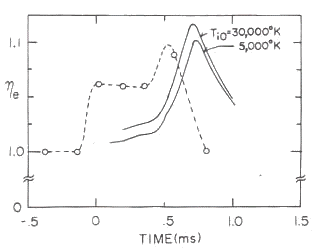
Fig.24 Time transience of the anisotropy. The solid lines indicate the theoretical transitions [reference (4)] Experimental condition is that the neutral gas pressure (Argon gas) is p=0.22 mTorr and the mirror ratio of the externally applied magnetic mirror field is |
Fig.25 The same as the left [reference (4)]
Experimental condition is that the neutral gas pressure (Argon gas) is p=0.30 mTorr and the mirror ratio of the externally applied magnetic mirror field is |
|
|
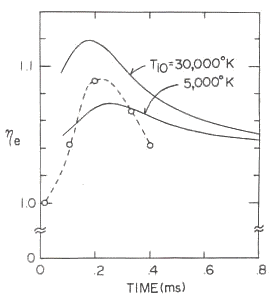
Fig.26 Tthe same as the left [reference (4)]
Experimental condition is that the neutral gas pressure (Argon gas) is p=0.46 mTorr and the mirror ratio of the externally applied magnetic mirror field is |
|
The results mentioned above in TEPSON machine have been reported in Annual Meeting of the Physical Society of Japan in 1976 , doctorial thesis in 1977 and Annual Meeting of the Physical Society of Japan in 1975 .
|
|
|
|
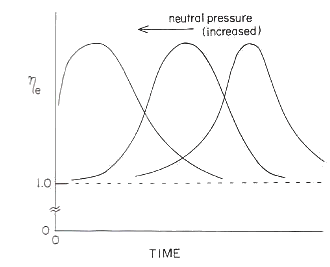
Fig.27 Neutral gas pressure dependency
of time transient of anisotropy |
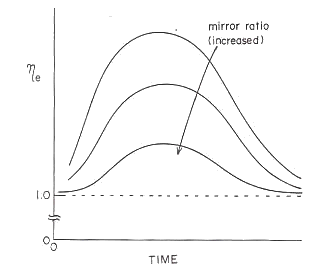
Fig.28 Mirror ratio dependency to time transient
of anisotropy |
|
6. Conclusion
The measurement of anisotropy of electron temperature or anisotropy of electron distribution function is performed in both of stationary and after-glow plasmas.
[Published Theses]
(1) N. Yamamoto, Y. Hatta, H. Aikawa and H. Ikegami: "Measurement of a mirror probe method of anisotropy of the electron distribution function of afterglow plasma confined in a magnetic mirror field", Physical Review A, Vol.13, No.4, pp.1543-1547 (1978).
|
_ returning to the former page with 'return' of browser _
or
_ returning to the home page with the following button _
| HOME |
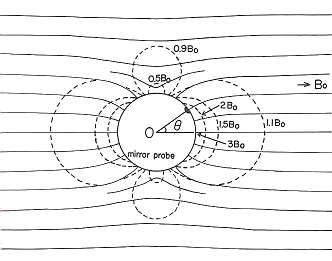
 the angle between the externally applied magnetic field line and the orthogonal direction of the spot surface can be varied from 70 degrees of angle to zero. Therefore, the local magnetic mirror ratio can be varied from one to three. The magnetic field lines surrounding the ferromagnetic sphere are shown in Fig.4.
the angle between the externally applied magnetic field line and the orthogonal direction of the spot surface can be varied from 70 degrees of angle to zero. Therefore, the local magnetic mirror ratio can be varied from one to three. The magnetic field lines surrounding the ferromagnetic sphere are shown in Fig.4.
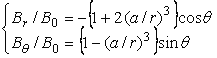 . (14)
. (14)
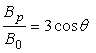 . (17)
. (17)
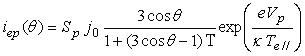 . (21)
. (21)
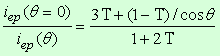 , (22)
, (22)
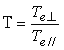 . (23)
. (23)
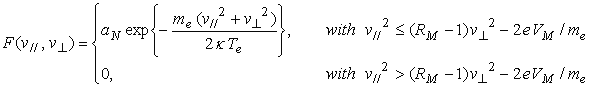 , (24)
, (24)