TDCC Laboratory
| HOME | JAPANESE |
Equation of Egg Shaped Curve III (Egg Shaped Curve I proposed by Mr. Asai)
Mr. Yasuyuki ASAI (Machida city, Tokyo, Japan) and Nobuo YAMAMOTO
Mr. Yasuyuki ASAI has informed another novel type of an egg shaped curve to Yamamoto in July, 2009.
This thesis is described by YAMAMOTO in account of the equation of the egg shaped curve proposed by him,
and advanced calculations are performed also by YAMAMOTO.
|
This site is introduced in
Bounds of rotated egg? ,
Principal room ,
[Curve-12] Let's draw an egg curve ,
GENERATING AVIAN EGG USING RATIONAL BEZIER QUADRATIC CURVES .
|
|
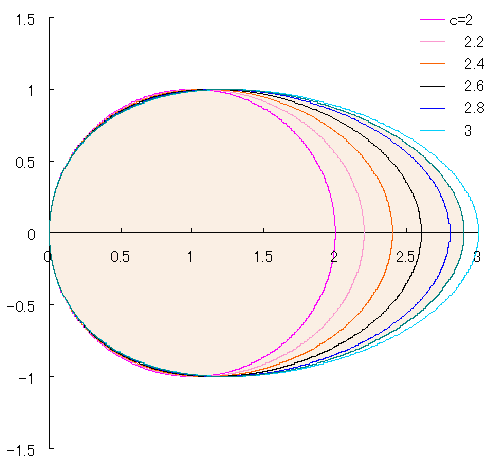
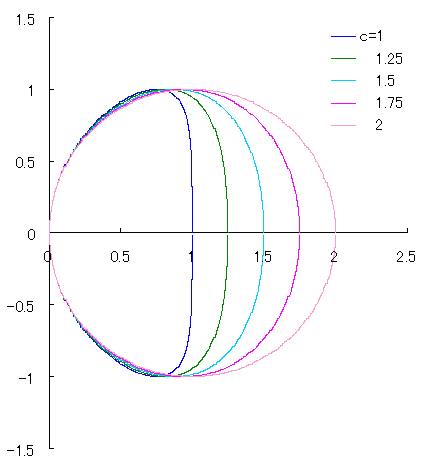
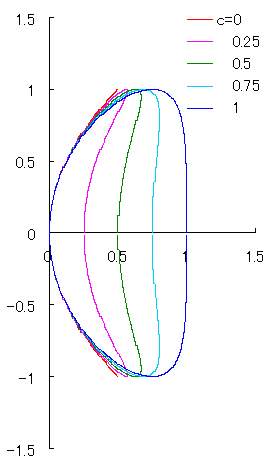
The equation expressing another novel type of egg shaped curve
proposed by Mr. Yasuyuki ASAI is written in the following;
|
|
|
|
|
|
|
|
|
|
 |
|
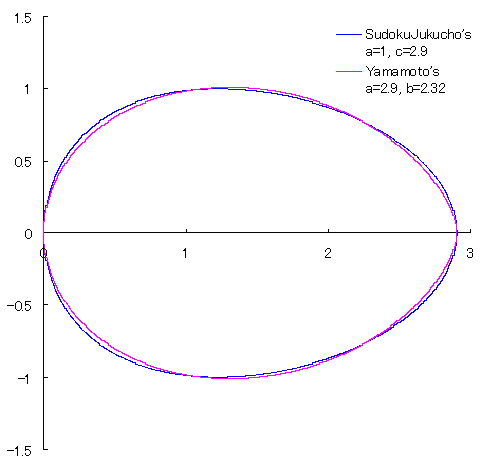
and Yamamoto's. Here, Yamamoto's is displaced by some values and then, is reversed in the x direction for the comparison. |
_ returning to the page which opened just before with 'return' of browser _
or
_ returning to the HOME with the following button _
| HOME |