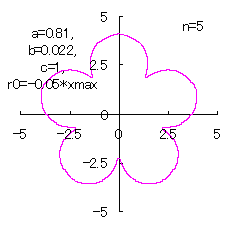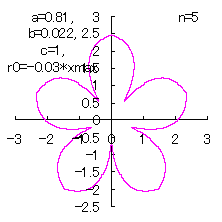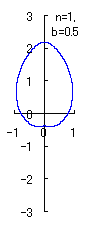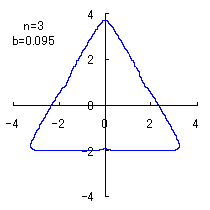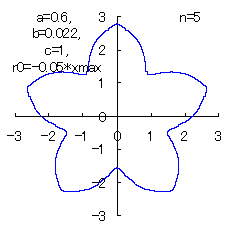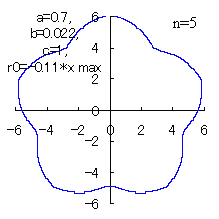|
Using the way described above, Eq.(1) is rewritten as in the following;
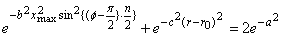 .
(6) .
(6)
From the above equation, we obtain the radius vector r in the expression of a asteroid or a shape of a flower having n number of corners as
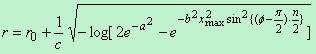 .
(7) .
(7)
For the expression in the orthogonal coordinates, the usual variables conversion is applied as
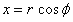 ,
(8) ,
(8)
and
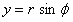 .
(9) .
(9)
By calculating Eqs.(7), (8) and (9) with the use of computer as giving the value of 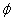 in the range of
in the range of 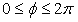 , we obtain the figures as shown below. , we obtain the figures as shown below.
(1) In the case of star graphics (n=5)
 When the above figures are painted, the following ones are drawn.
When the above figures are painted, the following ones are drawn.






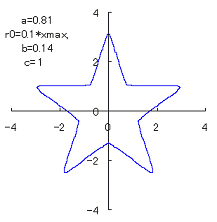
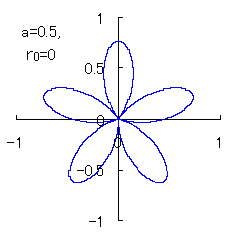
(2) In the case that a=0.81,  =0.1* =0.1*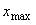 ,
b=0.14 and c=1 ,
b=0.14 and c=1
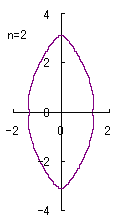
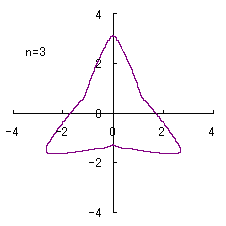
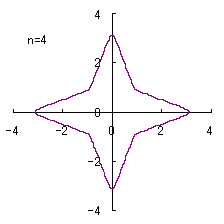
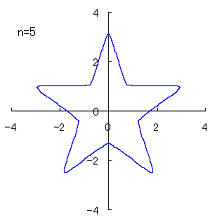
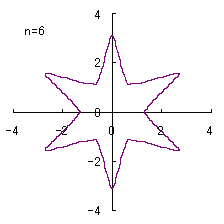
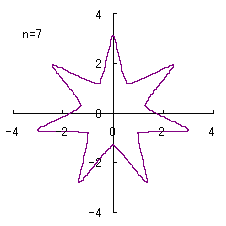
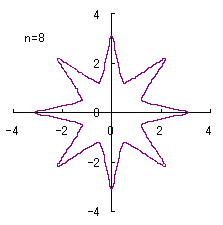
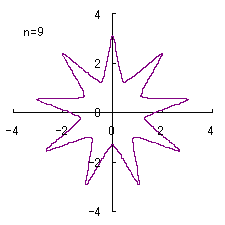
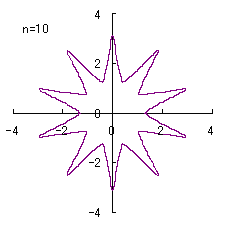
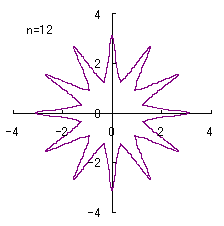
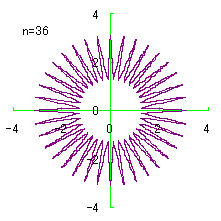 When the above figures are painted, the following ones are drawn.
When the above figures are painted, the following ones are drawn.












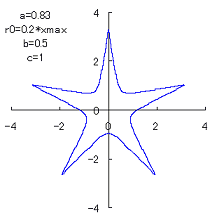
(3) In the case that a=0.83,  =0.5* =0.5*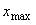 and b=c=1
and b=c=1
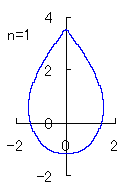
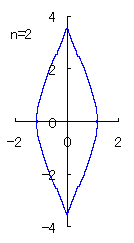
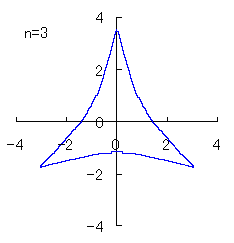
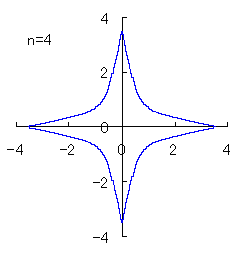
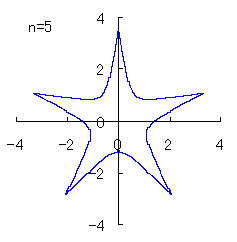
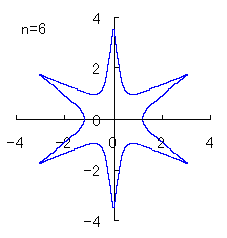
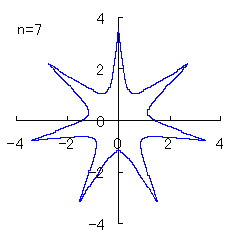
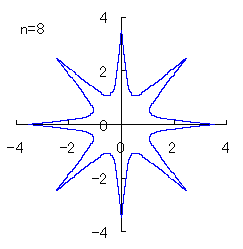
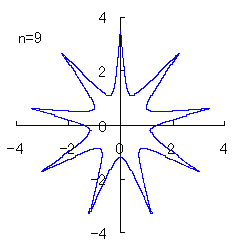
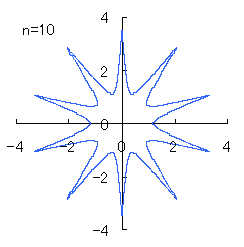
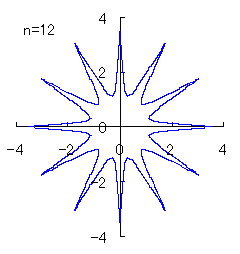
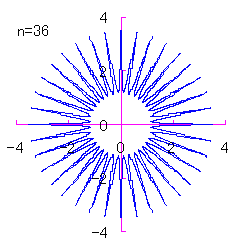 When the above figures are painted, the following ones are drawn.
When the above figures are painted, the following ones are drawn.

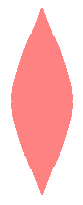
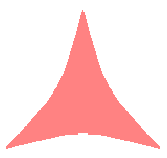









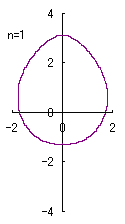
(4) In the case that a=0.83,  =0 and b=c=1 =0 and b=c=1
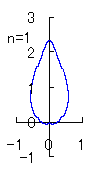
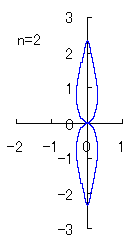
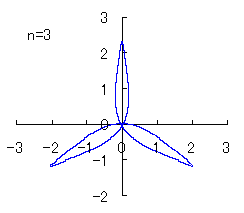
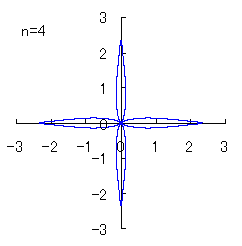
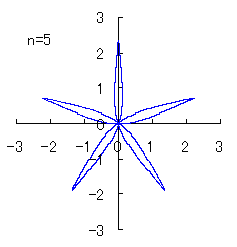
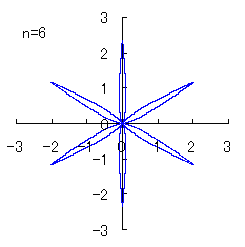
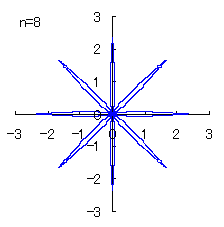
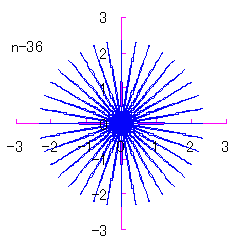
When the above figures are painted, the following ones are drawn.







(5) In the case that n=5 and b=c=1
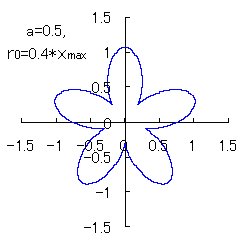
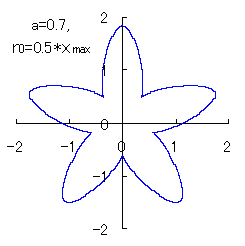
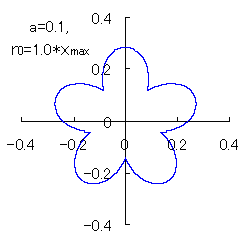
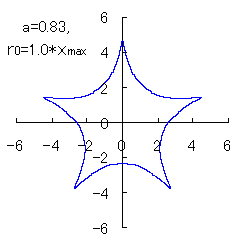 When the above figures are painted, the following ones are drawn.
When the above figures are painted, the following ones are drawn.





(6) In the case that n=5, a=0.7, b=0.2 and c=0.3
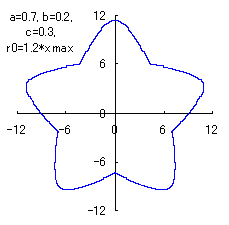
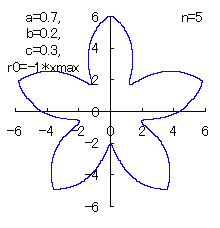
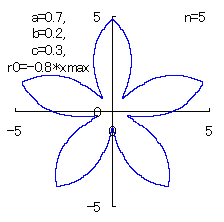
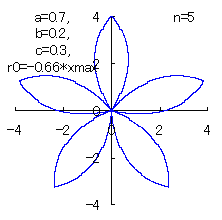
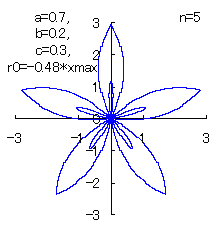
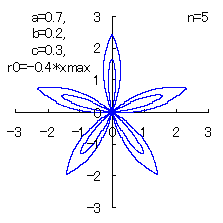
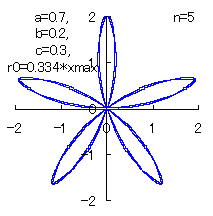
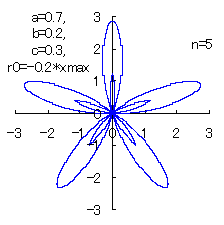 When the above figures are painted, the following ones are drawn.
When the above figures are painted, the following ones are drawn.








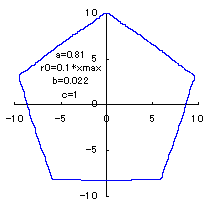
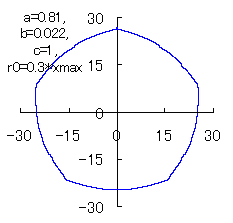
(7) In the case that n=5, a=0.81, b=0.022 and c=1 (There are also the cases of  <0.) <0.)
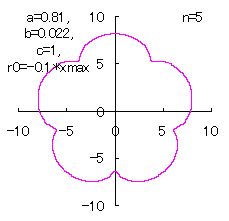
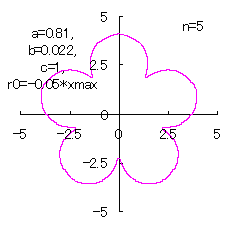
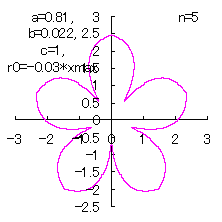
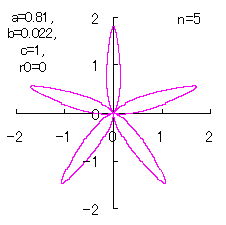
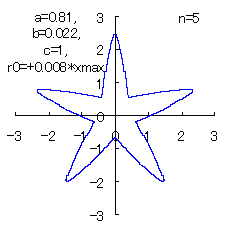
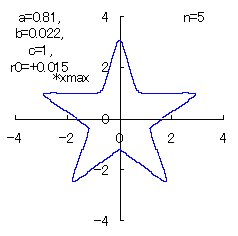
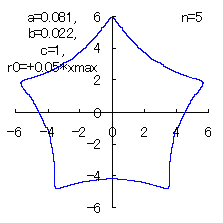
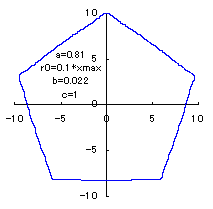

When the above figures are painted, the following ones are drawn.









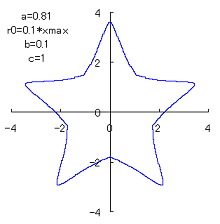
(8) In the case that a=0.81,  =0.1* =0.1* and c=1 and c=1
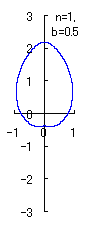
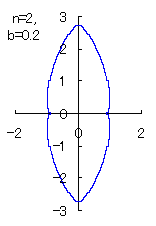
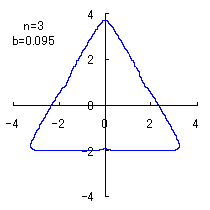
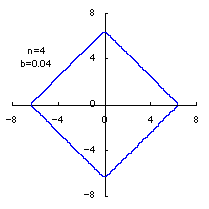

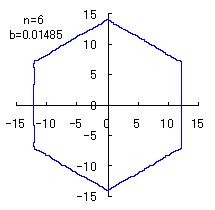
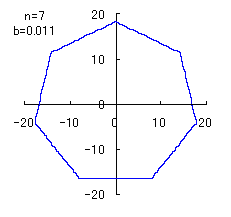
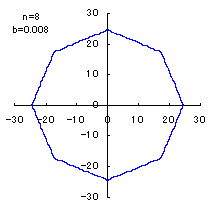
When the above figures are painted, the following ones are drawn.








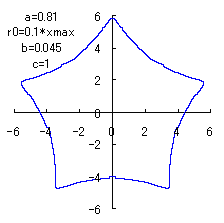
(9) In the case that a=0.81,  =0.1* =0.1*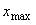 and c=1 (II) and c=1 (II)
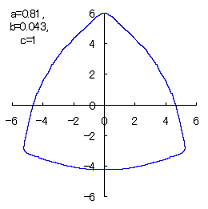
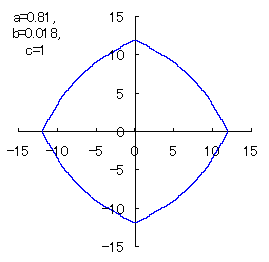
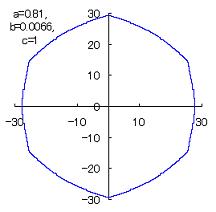 When the above figures are painted, the following ones are drawn.
When the above figures are painted, the following ones are drawn.




(10) In the case of the other parameters (There are also the cases of  <0.) <0.)
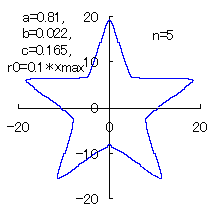
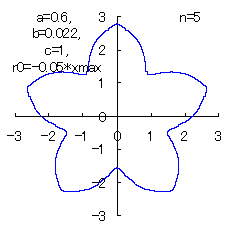
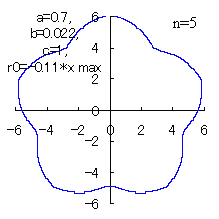
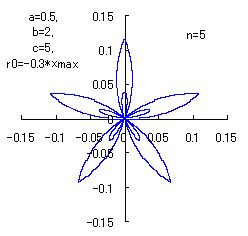
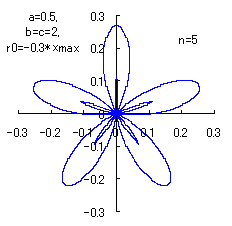
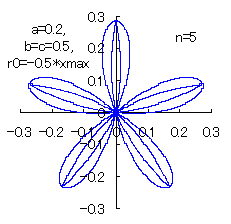
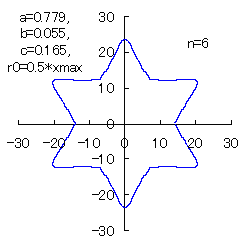
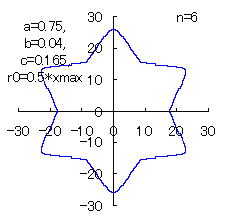
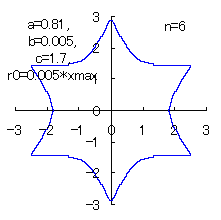
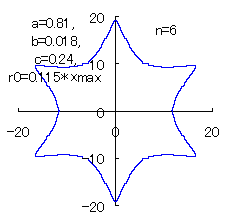
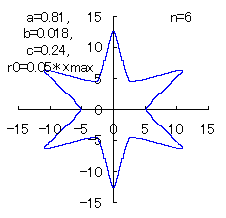 When the above figures are painted, the following ones are drawn.
When the above figures are painted, the following ones are drawn.











The various types of flower shapes are continued to
 . .
[Reference]
Formal Procedure
For the change of coordinates from the orthogonal ones (x, y) to the polar ones 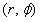 in Eq.(1),
the usual variables conversion is applied as in Eq.(1),
the usual variables conversion is applied as
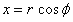 ,
(10) ,
(10)
and
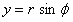 .
(11) .
(11)
In order that the display having four corners as shown in Fig.1 is expanded to one having the arbitrary n number of corners, and moreover,
in order that one of the corners is located on the top of the figure, the phase angle 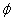 is replaced to
is replaced to 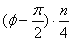 .
Thus, the conversion formulas are given by the followings instead of Eqs.(10) and (11). .
Thus, the conversion formulas are given by the followings instead of Eqs.(10) and (11).
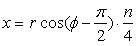 ,
(12) ,
(12)
and
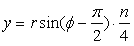 .
(13) .
(13)
If we substitute Eqs.(12) and (13) into Eq.(1), we obtain
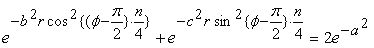 .
(14) .
(14)
where the constants a, b and c are the positive real numbers, and only the constant a is restricted by the follows;
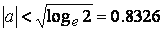 .
(15) .
(15)
By calculating Eq.(14) as giving the value of 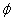 in the range of in the range of 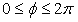 ,
the radius vector r should be obtained theoretically.
However, this calculation is generally impossible analytically except for a limited value of n. ,
the radius vector r should be obtained theoretically.
However, this calculation is generally impossible analytically except for a limited value of n.
|
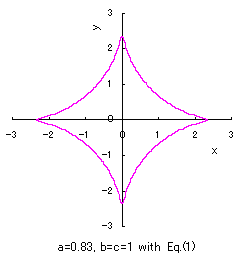
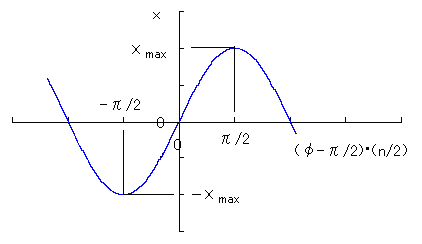















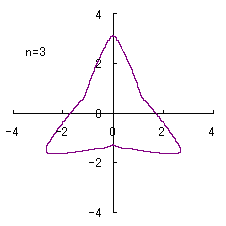





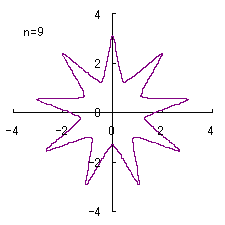














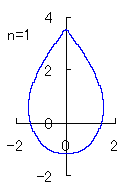






















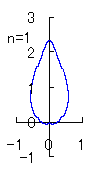
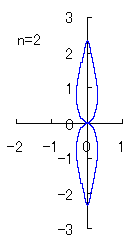

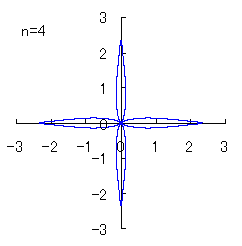












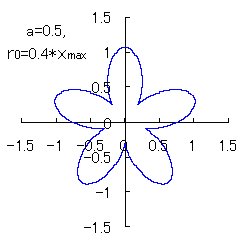
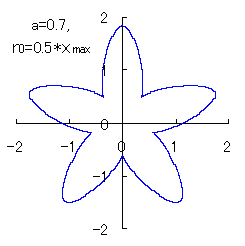
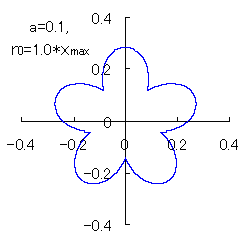
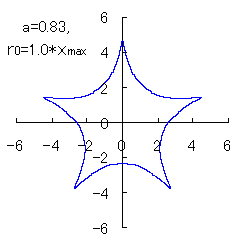





















 <0.)
<0.)