(1)    山本が提唱した卵形曲線で b=0.7a の場合を、 レオナルド・ダ・ビンチのウィトルウィウス的人体図に描いたところ、 卵形曲線が４個の手の先と２個の脚の先と接することができると同時に、正方形に内接するように描くことができる、ということを見出した。 それを図１に示す。 卵形曲線が正方形に内接しているということは、円の半径と正方形の辺の比が黄金比に近いといわれてきたので、 円の半径と卵形曲線の短径との比が黄金比 1 : = 1 : 1.6180339887 に近いことを意味している。

    上記の他に、種々の図形をウィトルウィウス的人体図に書き込んだ試行例を図2から図5に示す。

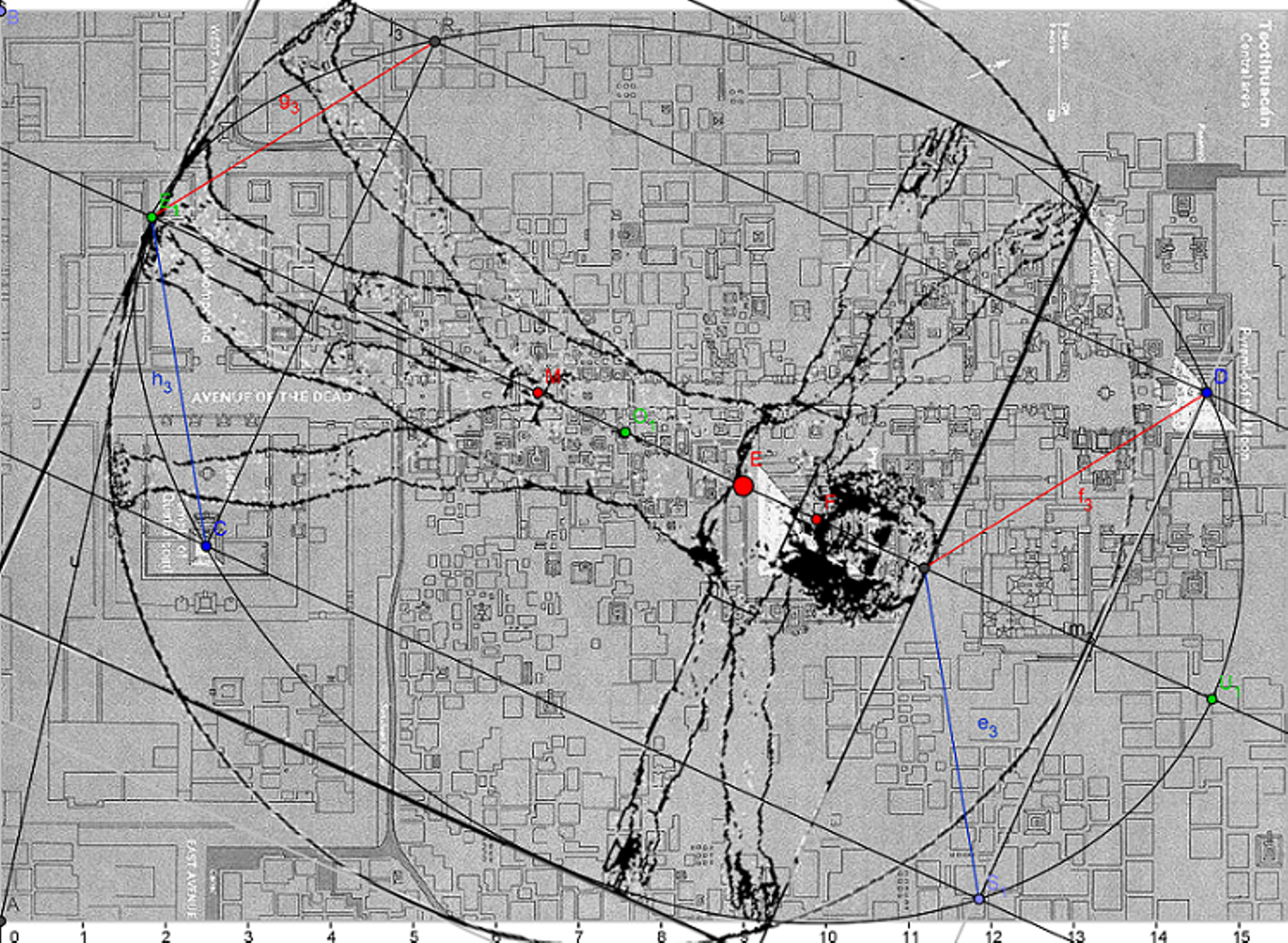
(2)    次に、レオナルド・ダ・ビンチのウィトルウィウス的人体図だけでなく、新たな長方形/b=0.7aのときの卵形曲線が、メキシコのテオティワカン古代都市のの地図上に適用できることが分かりました。それを図6に示します。
    図6中、大きな赤い点 E はテオティワカンの3つのピラミッドの平均値（C + F+ D）/3 です。 卵形曲線の長軸は E, F を通っています。M は「グルーポ・バイキング」と呼ばれる都市の中心地であり、また、ウィトルウィウス広場の中心地です。 ピラミッド C 及び D は卵形曲線上に存在します。 新たな長方形が C と D から作られ、その高さはウィトルウィウス正方形よりも小さいけれども、その幅はウィトルウィウス正方形と同じ幅を示すだけでなく、人の足先の歩幅にも等しくなっています。
    それゆえ、レオナルド・ダ・ビンチのウィトルウィウス的人体図は、古代都市への適用の一つの提案であり、新たな長方形/卵形曲線は、もう一つの提案です。

(3)    上記(1)に引き続き、レオナルド・ダ・ビンチのウィトルウィウス的人体図に新たな図形の組み合わせが2016年6月6日に見付かりました。それは、下図（図 7）に示されるように、5角形と8角形から成るものです。
    ダ・ビンチの人体図の方形の高さは X / tangent18、そして、ダ・ビンチの人体図の円の高さは 2X / tangent18 － X / tangent22.5 です。     上に書いた方形の高さは以下のように導かれます。     tangent 18 の値は 1/3.077 なので、正五角形の辺の長さとその正五角形の高さの比は 3.077 です。なお、数値 18 は、水平軸と五角形の右上の辺の間の角度（度）です。
    そして、五角形の半分をXとすると、五角形の高さは3.077 Xです。図に見られるように、ダ・ビンチ正方形の高さとダ・ビンチの円の半径との比は、0.618　（黄金比）よりも 0.6035　（正方形の回転から導かれる）に近い。ここでは、半径を中間値の 0.6077として扱うことにします。すると、円の直径は、正方形の高さ 0.6077 の2倍の 1.2155 となります。
    正八角形の辺の長さと同じ八角形の高さとの比は、tan 22.5°が 1/2.414 であるため、2.414 です。ここで、22.5°は、上の頂点の1つとその対角となる下の頂点との両方を切る線と垂線となす角度です。そのとき、八角形の一辺が（五角形の半辺と同じように） X である場合、五角形の高さと八角形の高さの比は0.7844です。五角形の高さがダ・ビンチの正方形の高さと等しく、1 に等しいので、最初の等式は 3.077 X = 1 となります。そのとき、円の直径は1.2155 であり、八角形の高さは 0.7844 です（そして、五角形の高さの2倍から八角形の高さを引くと、2 - 0.7844 = 1.2155 であり、これはダ・ビンチの円の直径に等しい）。
    五角形の高さの2倍から五角形の高さを引いくと 2 * 3.077X - 2.414X （ここで、X は常に八角形の1辺であり、五角形の半分の辺でもある）となり、それで、ダ・ビンチの円の高さは 2X /tan 18°- X /tan 22.5°= 2 * 3.077 X - 2.414 X = 1.2155 です。ここに、tan 18°= 1/3.077、tan 22.5°= 1/2.414 です。
    卵形曲線の関係式 b = 0.6967 a （第1節の卵形曲線に述べた式 b = 0.7a から近似の値を使います）を用いると、ダ・ビンチの正方形の辺は 2 /（1 + √3）（ = X /tan 18°）となります。こうして、我々は、1 /（1 + √3）の長さの辺を持つ正方形と六角形とともに、卵の高さ（= 1）に到達します。

(4)    上の(3)節を継続し、さらに発展させて、五角形と八角形、さらに、卵形曲線に関係付けられるダ・ビンチの人体図が新たな論文として に解析しました。
    なお、この論文で、参考文献[1]から[7]の卵形曲線が順に参照されています。

参考文献
[1] 山本の卵形曲線 (1)

[2] 伊藤氏の卵形曲線

[3] 浅井氏のの卵形曲線 (3)

[4] 浅井氏の卵形曲線 (2)

[5] 浅井氏の卵形曲線 (1)

[6] 山本の卵形曲線 (2)

[7] 山本の卵形曲線 (3)